给学生展示才华的空间

摘 要：给学生展示才华的空间，就要求教师把课堂搭建成一个平台，以点拨、引航的方式，使学生在已知的基础上探索未知。通过讨论、合作等多种形式，展示个人才华，体味探索的奥秘和成功的喜悦，从而激发创造能力。

关键词：展示才华；空间；创设情境；互助学习；设置悬念；体验

课堂是教学的主阵地，也是学生学习的主要营地。课堂45分钟内，师生可以共同在知识的海洋中遨游，乘风破浪。展现魅力的应该是教师呢，还是学生？答案是肯定的，学生是遨游的主体，教师只能是个导游。所以，应当给学生充分展示自我才华的空间，让他们在知识的海洋中游畅淋漓，直至理想的彼岸。

给学生展示才华的空间，就要求教师观念不断更新，认识能力不断提高，教师包办和口若悬河地展示自己的才华，只能照猫画虎地教给学生知识，不经过学生自己分析、思维，是不可能产生智慧的火花和成功的喜悦的，也不可能有探索精神和创新能力。

在新理念下的数学教学中，教师的职责在于向学生提供从事数学活动的机会，在活动中激发学生的学习潜能，引导学生积极从事自主探索、合作交流与实践创新。精心设计每一个问题，每一次对话，每一个动手操作，每一次合作，每一次辩论，尽力让学生自己说，自己思考，自己做。

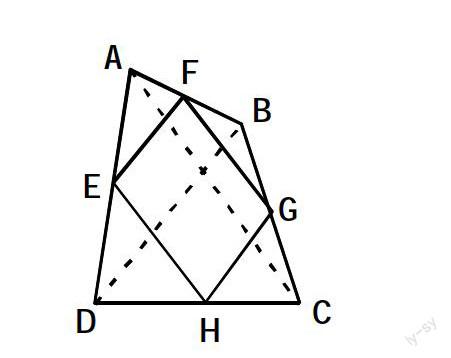
案例一：创设情境，因势利导

教师：同学们，今天是几月几号？生：9月30日。

教师：明天是我们伟大祖国的生日很多同学参与了学校的装饰庆典活动。有一位同学需要从任意四边形纸片上取一个平行四边形用作装饰材料，我们帮他想一想，怎样做才能既简单又可靠？

学生：（讨论得出）顺次联结原四边形各边中点得到的新四边形是平行四边形。

教师：我们能否给这个得到的新四边形一个合适的命名？

学生甲：顺次联结四边形各边中点得到的四边形——中点四边形。

教师：所得的是平行四边形吗？请同学们证明自己的判断。

（甲学生板演，其他学生写出证明过程。）

∵FG■■AC且EH■■AC∴EH■FG∴四边形EFGH是平行四边形。

教师：这个证明的关键是什么？

学生乙：（经过讨论得出）作四边形的对角线，把四边形化为两个三角形，然后运用三角形的中位线定理证明一组对边平行且相等，这样的四边形是平行四边形。

教师：如果我们改变原四边形的形状，中点四边形会发生变化吗？

学生：独立思考，可以动手绘画，也可以互相讨论。

学生展示结论。

平行四边形的中点四边形是平行四边形。

矩形的中点四边形是菱形。

菱形的中点四边形是矩形。

正方形的中点四边形是正方形。

教师：原四边形的什么条件起决定作用？你能不能提出新猜想或得出新结论？

学生再次分组讨论，动手绘画，得出对角线起决定作用。结论如下图。

图1：原四边形对角线互相垂直时，顺次联结各边中点得到的平行四边形是矩形。

图2：原四边形对角线相等时，顺次联结四边形各边中点得到的四边形是菱形。

图3：原四边形对角线互相垂直且相等时，顺次联结四边形各边中点得到的四边形是正方形。

教师汇总反思：这节课没有教师平铺直叙的讲解，也没有学生自学教材理解记忆的固定模式，而是创设情境“从改变形状”入手，由学生自己“提出猜想”，以“问题驱动”的方式开展互助学习。整堂课形成了“提出猜想、验证猜想、抽象概括、反思提高”的学习模块，给学生提供了比较充分的活动时间和空间。

案例二：举一反三，互助学习

教师：你能由长方形剪出一个三角形，并使它的面积是长方形的一半吗？（要求剪出的三角形一边落在长方形的边上）

学生：（全班哗然）做对角线。

教师追问：还有其他方法吗？

全班学生安静了。

教师又问：你能说出三种以上吗？

学生分组动手操作并讨论，各组結果板演如下：

∴△ABC面积就是长方形面积的一半

教师：比较一下，你们发现了什么呢？

学生抢答1：所得三角形底和高都与原长方形的长、宽对应

相等。

抢答2：所得三角形面积都相等。

抢答3：所得三角形不一定全等。

抢答4：等底、等高的三角形不一定全等，但面积一定相等。……

教师汇总反思：通过从这个简单问题入手，并设置几个挑战性的问题，激发学生的浓厚兴趣和深入思考，学生的主体地位体现突出；关注学生学习过程中的情感体验，使学生始终保持良好的学习状态；构建和谐、宽松的课堂气氛，使学生主动进行数学

思考。

案例三：设置悬念，激发探求欲望

路边拐角处有一块方角形菜地，要平均分给两家，为了便于管理，想用一条直线分割开来，你能帮他们分一下吗？

■

学生深思：（有难度）

有学生说：要是矩形就好了！教师追问：真要是变成矩形菜地，谁会分割？

学生抢答板演：

教师：你们怎样准确画出这条线，有道理吗？

学生甲：矩形是轴对称图形，对边中点的连线平分矩形。如图4、5

学生乙：矩形是中心对称图形，过中心的任意一条直线平分矩形。如图6、7、8

教师：同学们说得非常好，那么能否把方角形转化成两矩形呢？试试看。

学生讨论研究，豁然开朗。

（1）割图法变矩形 （2）补图法变矩形

教师汇总反思：设置悬念能在一定的空间、时间内激发学生的探求欲望。通过问题的层层明朗化，学生可以体会到探求过程的艰辛和成功的喜悦，从而进一步增强学习的内动力，并充分展示自我才华。

人们都需要发挥自己的潜能，表现自己的才能，从中得到最大的满足。实践告诉我们，教学过程尽可能地创造机会，让学生体验思维的绝妙，体验推理的严谨，体验语言的魅力，体验发明发现的伟大及成功的喜悦，这样学生的个性创造性才能不断地发展。我想，能有一个个具有积极、健康、发展心态的学生，才是我们教育的成功所在。

编辑 谢尾合