多球平衡问题

邱为钢

（湖州师范学院理学院，浙江 湖州 313000）

多球平衡问题是中学物理竞赛训练常见题目，理想模型是多个光滑的球，约束在曲面（柱面或半球面）内，或者用绳子悬挂起来，求满足什么样的条件达到平衡.问题关键是求解受力平衡方程，常用方法是几何和三角函数法.其实用代数法（解析几何法）更加直观简单，且容易推广到三维空间.代数法是基于这样的思想：如果一个物理矢量，例如力，已经确定与一个几何矢量方向相同，那么这个物理矢量必定与这个几何矢量成比例关系，它们的分量之间也成比例关系，且分量之间的比例系数相同.这个比例系数是常数，有量纲.为集中讨论，本文只考虑悬挂多球平衡问题.

先讨论3球问题，用两个相同长度的绳子拴住两个一样的球，挂在天花板上的同一顶点上，两球接触，然后再把第3个球放在两球上，松手，看这3个球能否达到平衡.（这是假想模型，你试着做做实验看呢，有问题吗？）假定3球达到平衡，设第3个球的球心O为原点，坐标为（0，0），半径为r，质量为m.前两个球球心为O1，O2坐标分别为（x，－y），（－x，－y），半径为R，质量为M.天花板上顶点H坐标为（0，h），绳子长度为l，如图1所示.

两球的球心距离为OO1＝R＋r，即有

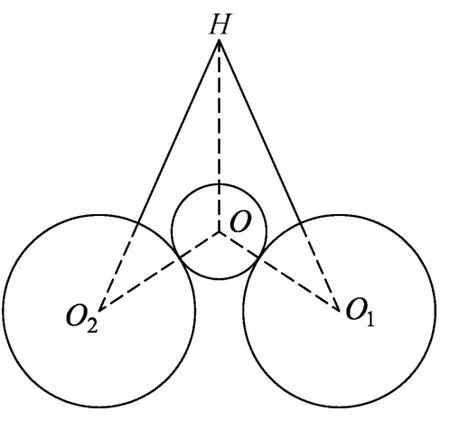
图1 悬挂了球示意图

顶点到球心距离为HO1＝l＋R，即有

绳子中张力方向与矢量相同，由对称性，设比例系数都为λ，即

两球的相互作用力方向与矢量相同，由对称性，设比例系数都为k，即

3个球受力平衡，两个绳子中张力和3个小球重力矢量和为0，即

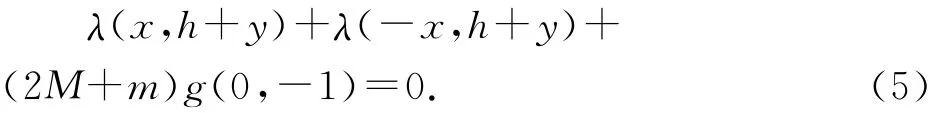
对第1个小球来说，绳子张力，重力和第3个小球对它的作用力之和为0，即

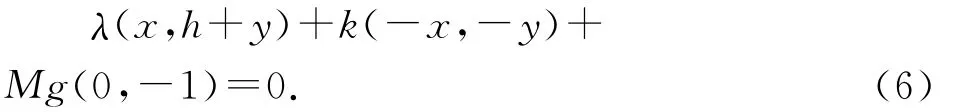
由（6）式解得

由（5）式解得

第3个小球到绳子的距离d为

考虑实际约束条件，第3个小球碰不到绳子，即d＞r，或者

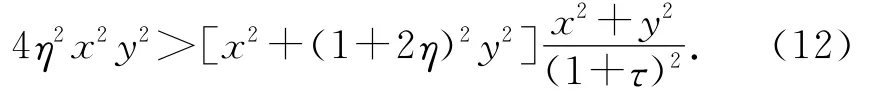
不等式（12）成立的必要条件是对应的判别式大于等于0，计算得到

（13）式含义是质量比η越大，半径比τ越大，越容易达到平衡位形，这与实际经验相符.如果3个小球完全一样，那么（13）式取等号，这就意味着3球平衡问题只能取一种平衡位形，与文献［1］的结论一致.

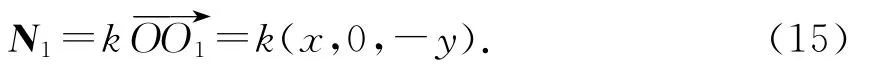
4球受力平衡，3个绳子中张力和4个小球重力矢量和为0，即

对第1个小球来说，绳子张力，重力和第4个小球对它的作用力之和为0，即

由（18）式解得

由（17）式解得

由（19）和（20）式解得

第4个小球到绳子的距离d是

考虑实际约束条件，第4个小球碰不到绳子，即d＞r，或者

（23）式两边平方，并利用（1）和（2）式，且定义半径比为τ＝R/r，那么（23）式化为

不等式（24）成立的必要条件是对应的判别式大于等于零，计算得到

对比（25）和（13）式，说明实际4个小球比理想模型3个小球更加容易达到平衡，这也符合实际经验.如果4个小球完全一样，那么（25）式成立，这就意味着4球体系可以存在平衡位形，推广了文献［1］的结论.各个参数，例如坐标，张力等可以求解（1），（2），（19），（20）得到，不再具体给出.

由此看来，考虑一个物理问题，我们必须从实际出发，而不是只研究简化模型，例如实际问题是4球平衡，而为什么常见题目只考虑3球？还有，对于理论模型，能不能真的去实验一下，看看会不会发生你意料不到的问题.有问题了，就有可能有新的发现.

1 黄尚鹏.警惕3球平衡问题的陷阱［J］.物理通报，2014（11）：54－56.