对一道几何证题中辅助线画法的物理解释

罗春焱

（重庆綦江区三江中学，重庆 401431）

中学学科教学中，由于受到学科界域的限制，教师往往只从自己从事的单一学科去寻找答案，而忽视与其他学科的横向联系，忽视与其他学科的相互交叉.对某些问题可以从多学科角度做出理解，下面笔者通过一道几何证题中涉及辅助线画法的学生疑问的解答过程来加以说明，以期能起抛砖引玉的作用.

1 几何题目及其证明

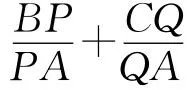
证明：如图2所示，连接AG并延长与BC交于D；延长PQ，过B、D、A、C4点作PQ的垂线，其垂足分别为E、T、H、F.

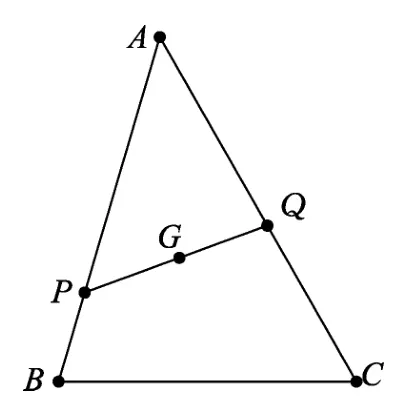
图1

图2

因为△PEB∽△PHA，所以

又因为△QFC∽△QHA，△DTG∽△AHG，则

由于D是BC的中点，因而DT是梯形BEFC的中位线.所以，

联立（1）～（4）式可得

2 学生疑问及其对疑问的物理解释

通过证明，问题已得到解决，然而，有学生却提出“在该题的证明中，为什么要添加这样的辅助线呢？”的疑问.对于这个新问题，数学教师通常会回答“只要同学们多加练习，见多识广，就可熟能生巧”.针对这一疑问，笔者引导学生进行如下的教学探讨.

师：同学们，这样作辅助线有科学依据吗？现在，我想用物理方法来解释这个问题，请同学们跟我一起共同来完成.

生：保持沉默.

师：大家想一想：在物理学中，三角形的实体模型是怎样的呢？

生：可以是一块均质的三角形薄板；也可以是3个等质的小球用3根轻直杆连接而成.

师：我们是否可以用“3个等质小球用3根轻直杆连接”的三角形实体模型来解决以上关于辅助线画法的问题呢？

生：可以，因为我们曾经做过2个物理实验：一个是悬挂法测重心实验；另一个是验证杠杆平衡条件实验.如果将2个实验结合起来似乎就能解决这个问题了.

师：很好！那么究竟应该怎么做呢？

生：走向黑板，画出图3与图4的几何图形后说：将A球用细线悬挂于O点，由悬挂法测重心实验知道，当ABC整体静止时，三角形ABC的重心G必在竖直线OA上（图3）.同理，将Q点用细线悬挂于O，当ABC整体静止时，则三角形ABC的重心G也必在竖直线OQ上（图4）.在图4中，我们就可以用杠杆平衡条件（A球的重力沿逆时针方向的力矩等于B、C两球的重力沿顺时针方向的力矩的代数和）列方程来加以解决.

设A、B、C3个小球的质量均为m.如图4所示，由杠杆平衡条件得

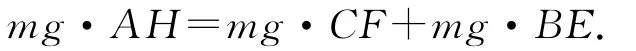
故AH＝CF＋BE.

又因为△PEB∽△PHA，

又因为△QFC∽△QHA，

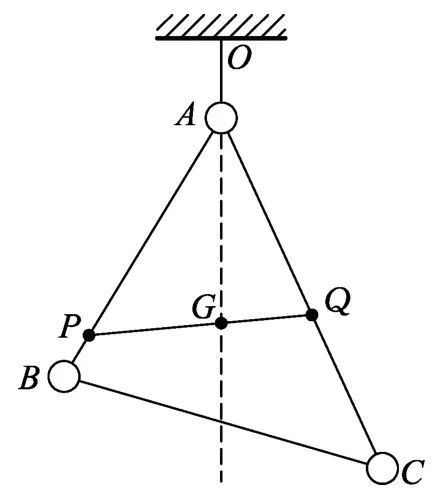
图3

图4

师：显而易见，结合物理知识来证明这道几何题更为简捷.由于力臂是支点（悬点O）到力的作用线的垂直距离.该问题中AH、BE、CF恰好分别是A、B、C3个小球重力的力臂.因此，我认为，这就是数学上证明该题的过程中，要过A、B、C3点分别作PQ的垂线（辅助线）的原因所在.

学生（全班齐声）：原来这道几何题还蕴藏着如此丰富的物理内涵，真是数理不分家.

3 教学启示与感悟

通过以上教学实例，笔者认为，在课堂教学中渗透不同学科知识是今后课程教学的新走向，它不仅符合当前高考综合学科考试的要求，也是对开设研究性课程的有力支持.教师要积极钻研相关学科教材，发掘不同学科知识在解决跨学科综合问题中的功效，促进不同学科知识间的融会贯通.这样，能唤起学生的学习兴趣，点燃学生智慧的火花，使学生的探究能力和创新能力得到充分的发展.