转变方法,加强初中数学思维能力的培养
2015-07-22吴建民
吴建民
【内容摘要】思维能力既抽象又具体,它虽然没有一个固定的模式与形态,却在指导学生顺利解决数学问题的过程中无处不在。为了能够切实提升初中学生解决复杂数学问题的能力,思维能力的培养提升至关重要。
【关键词】初中数学 学生 思维能力
对于初中数学学习来讲,最重要的能力是什么?知识能力固然不可或缺,但是,思维能力应当得到教师与学生更高级别的重视。如果将知识能力比作学生用来捡拾一个个散落珠子的能力,那么,思维能力则是用来指导学生怎样找到一条线来将这些珠子串起来。因此,思维能力在初中数学教学中居于一个统领地位,教师应当对之予以特别关注,并不断创新,转变方法,将数学思维能力进行细化,带领学生进行强化提高。
一、激发学习兴趣,鼓励独立习惯
思维能力训练的重要内容之一就是对学生独立思维的培养,这可以说是数学思维能力提升的第一步。虽然很多数学内容的教学是通过小组合作的形式进行教学的,但是,数学问题的解决最终还是要落到学生个人身上。尤其是在各种考试当中,面对复杂问题进行分析解答的还是学生自己。
在学习二次函数时,出示了这样一个问题:在篮球比赛中,运动员的各种状态会随着时间的变化而变化。经过调查发现:球员的状态y和时间t之间是有关系的,教师用多媒体展示y和t的关系图,并让学生独立思考:(1)比赛开始后第5分钟时与比赛开始后第30分钟时比较,哪个时间球员的状态更好?(2)你认为比赛开始多久后,球员的状态最好?
学生通过独立思考,很容易得出第1小题的答案。在做第2题时,学生碰到了障碍。老师让学生回顾一次函数,学生通过模仿一次函数的性质,求出y为多少时,其变化范围。“这是什么函数呢?它具有什么性质?”引发了学生探究的兴趣,进而开始学习新知。
独立思维是数学思维能力的基础。很多学生之所以表现出难以自主思考问题,其中一个重要原因便在于,他们在平时的知识学习过程中过于依赖教师的引导与讲解,而忽略了让自己先行独立思考的机会。因此,教师们需要为学生创造出足够的独立思维空间,让学生亲身感受这个过程,逐渐从生疏走向熟练。
二、善于总结提炼,掌握思维方法
从思维能力培养的实质部分来看,想要让学生数学思维能力得到显著提升,就必须将具体有效的思维方法传授给学生,让学生在面对具体问题时,能在头脑中快速匹配出相应的思维方式,并由此设计出正确的解决路径。
例如,为了向学生实际呈现数形结合的思维方法,我借助了这样一道习题:已知,二次函数y=x2-2(R+r)x+d2的图象与x轴无交点,且R和r分别是⊙O1与⊙O2的半径,d表示的是上述两个圆的圆心距。那么,这两个圆的位置关系是怎样的呢?看似不太相关的已知条件和问题,通过数形结合的方式,便可以通过4(R+r)2-4d2<0来得出(R+ r+d)(R+r-d)<0的结论,并且根据欲求结果,有方向地找出d与R+r之间的大小关系,进而得出两圆外离的结论。
想要让抽象的思维能力内容具体化,就需要教师将这部分内容通过分类来不断具化与细化,用不同的习题来对每一种思维方法的呈现与应用进行演示,让学生近距离地感受到每种思维方法的适用情况。这样的训练多了,学生们的意识当中自然会形成脉络清晰的数学思维。
三、理顺思考路径,提升思维品质
这里所说的思维品质,是与思维方法相对的,主要指的是学生在解决数学问题时的思维顺序。这是从形式上对于数学思维效果的保障。数学是一门对于思维逻辑的条理性和严谨性要求极高的学科。如果没有从思维设计环节做到毫无漏洞,那么,接下来再多的运算都是徒劳。可见提升思维品质的重要性。
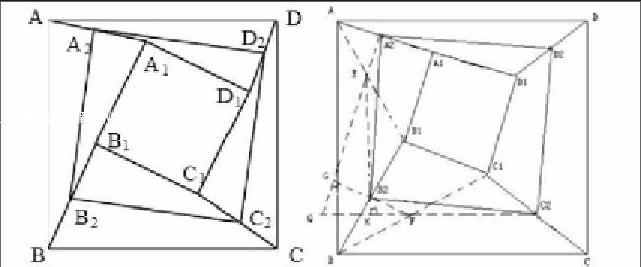
例如,学生们曾经接触过这样一个平面几何问题:已知,四边形ADCB以及四边形A1D1C1B1均为正方形,且点A2、D2、C2、B2分别为边AA1、DD1、CC1、BB1的中点(如下图左)。求证,四边形A2D2C2B2也是一个正方形。很多学生在看到这道习题的图形时,根本不知道该从何处入手。于是,我告诉学生,如果遇到从正向不知该怎样处理思路时,便可以尝试从反向进行逆推,即根据欲证明的结论,寻找自己所需要的条件,最后明确这些条件需要如何找到或创造,从而重组已知条件,或是通过构造辅助线使得问题得到解决。理解了这种思维方式之后,学生们积极实践,果然找到了正确的解答方式:连结AB1与BC1,并分别将其中点F、E同C2与A2相连,延长相交于点Q,连结B2E并延长,使之与QC2相交于点H,同理连结B2F并延长与QA2相交于点G(如下图右)。果然,原本复杂的问题一下子清晰起来了。
很多时候,学生在独立解决数学问题时会有顾此失彼的感觉,不知如何挑选和安排,导致眉毛胡子一把抓,思路反而越想越乱。当笔者有针对性地对于学生们的思维进行强调之后,大家在遇到数学问题时,明显没有那么手足无措了,而是可以按照教师所讲过的思维顺序,展开思考,思维质量大大提升。
总之,在面对过程复杂的数学问题时,教师和学生需要首先明确解答数学问题的正确顺序,即先从整体上设计出一个思维步骤,为具体解答做好计划,随后才进行具体地演算和推导。在一段时间的思维训练过后,学生们在处理数学问题的过程中,思路清晰高效了很多。这不仅提升了初中数学教学实效,还在潜移默化中增强了学生们的自信心和积极性。
(作者单位:江苏省苏州市吴江区七都中学)
