对《几何画板》应用于数学教学的几点思考
2015-07-07张行
张行
摘要:信息技术的普及大大方便了数学日常教学,提高了课堂效率和学习效果。笔者就《几何画板》在教学中的应用结合自身教学实际阐述了自己的观点。
关键词:《几何画板》;数学教学
中图分类号:G633.6文献标识码:A 文章编号:1992-7711(2015)09-072-1
随着信息技术的普及,初中数学不再抽象、枯燥,而变得形象生动、易学易懂起来。其中几何画板的应用尤其大大方便了数学教学。
一、《几何画板》在数学教学中的优点
1.激发学生的探索欲望。
教学中若使用常规工具(如纸、笔、圆规和直尺)画图,画出的图形是静态的,很容易掩盖一些重要的几何规律。《几何画板》可以在图形运动中动态地保持几何关系,可以运用它在变化的图形中发现恒定不变的几何规律,激发学生的探究欲望。
例如:在教学线段的中点时,对于问题:
(一)操作:画线段AB,在线段AB上任取一点C,取线段AC、BC的中点M、N
(二)观察与发现:线段MN与线段AB之间有何关系?
利用《几何画板》的度量和拖拽功能,可以直接发现线段MN与线段AB之间的数量关系,引起学生的兴趣,激发学生透过现象去思考本质,培养学生的推理能力与几何语言表达能力,对几何的入门教学有很大的帮助。
2.培养学生的抽象思维。
只有经过形象思维培养的人才会有很高的抽象思维,而《几何画板》就能将抽象的问题具体形象化,避免教师空洞的说教,从而逐步培养学生的抽象思维能力。
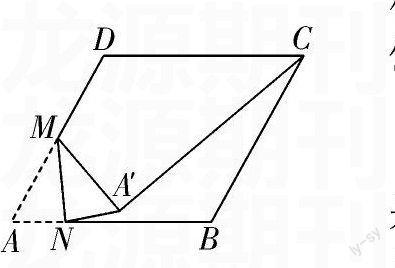
例如:如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是.
这道题需要将“N是AB边上一动点”这一条件,转化为“点A'的运动轨迹是以A为圆心、AM为半径的弧”,这样就很容易发现C、A'、M三点共线时A'C最短。这一转化过程借助《几何画板》中追踪点的功能就可以直观地发现点A'的运动轨迹,大大提高了教学效率。
3.提高学生的作图能力。
《几何画板》具有强大的作图功能,使用《几何画板》中的平移、旋转、缩放、反射、迭代等变换工具可以变换出各种复杂、精确的几何图案;利用轨迹、动画、隐藏/显示、系列、链接、参数选项等可以形成动感十足的几何动画和色彩斑斓的变色图案,让学生领略图形之美,培养作图的感觉,从而提高学生的作图能力。
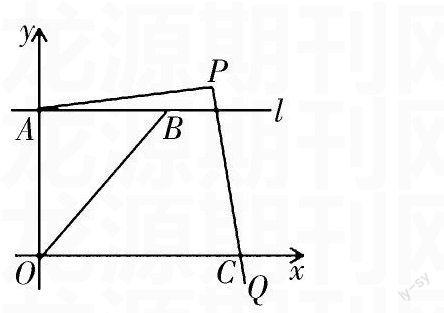
例如:(2014·绍兴25题)如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA∶PC的值.
(3)当动点P在直线OB上时,点D是直线OB与直线CA的交点,点E是直线CP与y轴的交点,若∠ACE=∠AEC,PD=2OD,求PA∶PC的值.
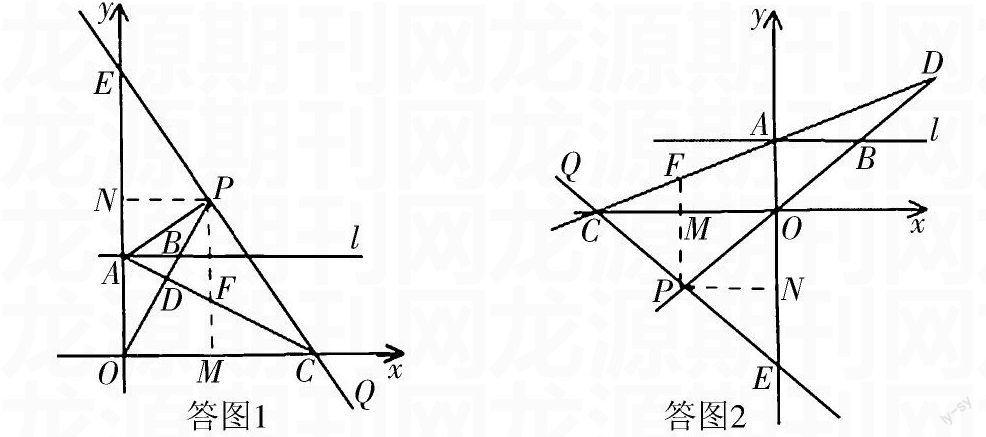
本题(1)(2)两问难度不大,而第(3)问将决定学生能否得高分,其中会准确的画出图形是成功解决问题(3)的关键。如能成功画出答图1、答图2则对正确分析问题、找到解法带来了便捷,如无法画出正确图形,尤其是答图2,则将与高分失之交臂。利用《几何画板》可以灵活调整图形的变化,从而找到符合题意的两种图形。
另外《几何画板》使用灵活,它可以在数学课件的制作中与多种软件整合使用,如Flash、Authorware、Powerpoint等,所以《几何画板》在数学教学中有着无与伦比的优势。
二、应用《几何画板》教学时应注意的几个方面
多媒体技术在教学中的应用应该是以教学的需要为基准,它是为教学服务的,在教学中起着辅助的作用,不应以多媒体的应用为主体而忽略了知识的传授,更应注意避免多媒体在教学中所起的负面影响。作为现代教育技术引入课堂的《几何画板》也应如此,只有恰当的应用才能收到良好的效果。
1.不可忽视抽象思维的培养。
一个学生如果不具备数学想象力,要想把数学学好是不可能的。所以不能完全将大脑的思考交给《几何画板》,在运用《几何画板》过程中,要充分地用它来引导学生的学习,让它帮助学生思考,而不是代替学生思考。作为教师要给予恰当的提示,通过计算机演示实验帮助学生完成思考过程,形成对知识的理解,而不是利用计算机直接地给出结论,否则会使学生养成过分依赖的习惯,不利于培养学生的抽象思维。
2.不可忽视作图方法的指导。
也许有时候手工作图需要花费很大力气才能画出一个符合题意的图形,而《几何画板》很轻松就可以画出来。但我们在教学中也不能完全借助于《几何画板》作图,有时候老师的手工作图可以给学生展示一个思考的过程,让学生感受到老师也需要不断调整图形最终才能成功,给学生起示范榜样的作用,从而培养学生克服困难的勇气和百折不挠的的意志。同时,教师在学生作图过程中,要及时提供方法指导,从而真正提高学生的作图能力。
