浅析含参量无穷积分一致收敛性的教学

钱淑英

（长治学院 数学系，山西 长治 046011）

浅析含参量无穷积分一致收敛性的教学

钱淑英

（长治学院 数学系，山西 长治 046011）

文章对含参量无穷积分一致收敛性的常用的判别方法进行系统的讨论，以便使学生较容易地掌握这部分内容，在教学中取得更好的教学效果。

含参量无穷积分；一致收敛；教学

含参量无穷积分是数学分析教学中的一个重要内容，它不仅是无穷积分的推广，也为我们研究和表达函数（特别是非初等函数）提供了有力工具，并为后面学习多元函数的积分打下了坚实的基础.一致收敛是含参量无穷积分的一个重要性质，有效地判别含参量无穷积分的一致收敛对进一步研究含参量无穷积分的性质起着重要的作用.但由于含参量无穷积分一致收敛性的判别方法灵活多变，学生们在学习中很难掌握.

1 利用定义法判别含参量无穷积分的一致收敛性

运用定义判别含参量无穷积分的一致收敛性关键在于寻找只与ε有关并且与参数无关的共同的N，在证明过程中常常用到适当放大的方法.

当y∈[2,+∞）时，有e-Ay≤e-2A，解不等式e-2A＜ ε，有于是取时，对一切y∈[2,+∞），有所以在y∈[2,+∞）上一致收敛.

2 判别含参量无穷积分一致收敛的充要条件

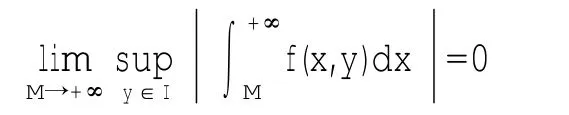
运用一致收敛的充要条件不仅可以判别含参量无穷积分在某个区间上一致收敛，还可以判别它在其它区间上非一致收敛[1]55，证明非一致收敛只需要证得

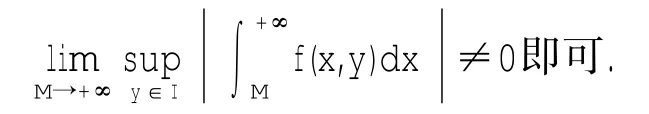
证明 取充分大的M＞0，有

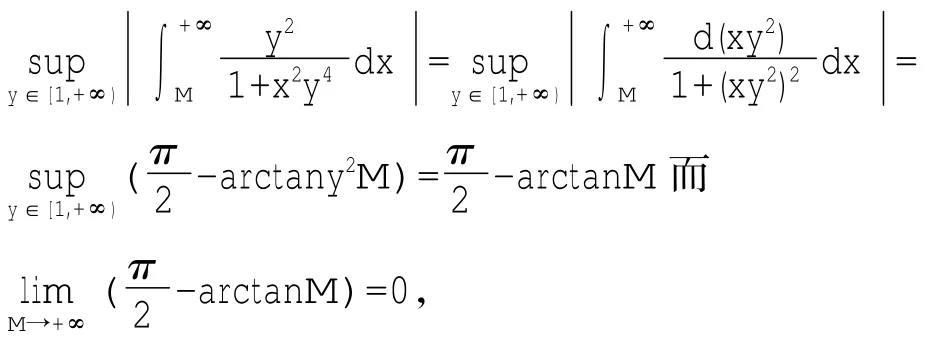
3 利用魏尔斯特拉斯M判别法判别含参量无穷积分一致收敛

4 利用柯西一致收敛准则判别含参量无穷积分一致收敛性

柯西一致收敛准则给出了判别含参量无穷积分一致收敛的一个充要条件，为我们判别含参量无穷积分一致收敛提供了一个有力工具.

对于任取的正数ε，存在正数A＞0，使得当A1＞A2＞A时，对一切y∈I，有

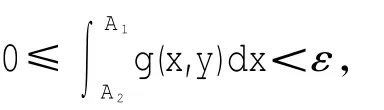
这个例题，也可以看作推广的魏尔斯特拉斯判别法.

5 利用狄利克雷判别法和阿贝尔判别法判别含参量无穷积分一致收敛

当含参量无穷积分的被积函数可以看成两个函数的乘积，并且这两个函数满足狄利克雷判别法或阿贝尔判别法的条件时，就可以利用狄利克雷判别法或阿贝尔判别法判别这个含参量无穷积分的一致收敛性.

6 利用级数判别法判别含参量无穷积分一致收敛

特别地，若函数f(x,y)为定义在无界区域R=[1,+∞）×I上的非负函数.如果f(x,y)关于x在[1,+∞）上单调递减，那么含参量无穷积分与函数项级数关于y在区间I上具有同样的一致收敛性[1].

运用函数项级数判别含参量无穷积分的一致收敛性，关键是要找到相应的函数项级数，并且能够比较容易的判别出此函数项级数是否一致收敛.

解 由题可得f(x,y)非负且关于x在(1,+∞)上单调递减，考虑函数项级数

∞

［1］裴礼文.数学分析中的典型问题与方法第二版［M］.北京：高等教育出版社,2006.

［2］华东师范大学数学系编.数学分析第三版［M］.北京：高等教育出版社,2001.

［3］刘红玉.含参变量无穷积分一致收敛性的判断技巧及应用［J］.牡丹江大学学报,2012,21(8):119-122.

（责任编辑 赵巨涛）

O172

A

1673-2015（2015）02-0057-03

2014—11—20

钱淑英（1964—）女,河北任邱人，副教授，主要从事基础数学教学法研究。