二维Ginzburg-Landan方程高精度分裂算法

高新忙，梁宗旗

（集美大学 理学院，厦门 361021）

二维Ginzburg-Landan方程高精度分裂算法

高新忙，梁宗旗

（集美大学 理学院，厦门 361021）

对于系数相对复杂的二维方程运用分裂法，分裂为非线性部分和线性部分，非线性部分可局部精确求解，线性部分采用有限差分法和紧致有限差分法处理，并综合采用分裂紧交替方向隐式法来求解，最后进行数值检验。

二维方程；分裂法；交替隐格式

1 引言

考虑下列二维方程：

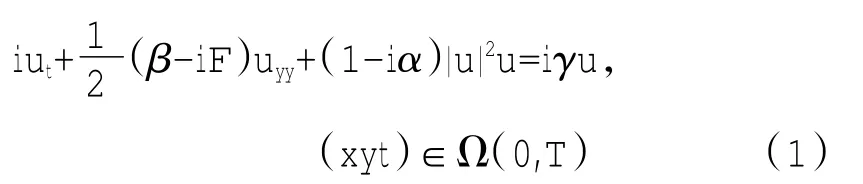
方程(简称GL)是一类较为复杂的方程.近年来，数学及物理工作者对GL方程的理论和性质进行了广泛的研究.此类型方程中许多系数均是复数类型的,计算时相对复杂.并且含有非线性项|u|2u，处于耗散状态，具有不稳定性，因而具有近似奇异性，是一个被称为具有在有限时间内形成局部奇性解的Hamiltonian方程.

2 数值解法

对方程（1）两边同乘i，并进行整理得：

利用二阶分裂方法，上式可分裂为：

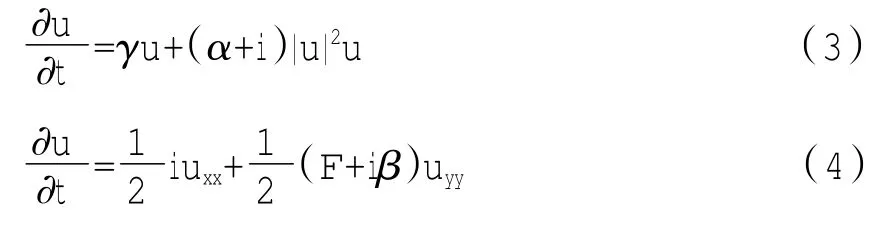
2.1 非线性部分处理

2.2 线性部分处理

本节内容构造两种格式，对于其解的精度性有不同的结果.分别构造差分格式与紧致差分格式.

格式：紧致差分格式.

将δx2,δy2分别用代换，整理得：

2.3 数值格式处理

对于综合处理格式，是求解微分的数值解的关键步骤.差分方法和紧致差分格式简单，不在此论述.以下详述隐格式分裂方法处理数值，具体如下：SSADI方法：交替方向隐式法.

第一步：

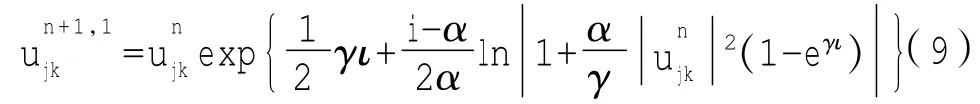
第二步：

第三步：

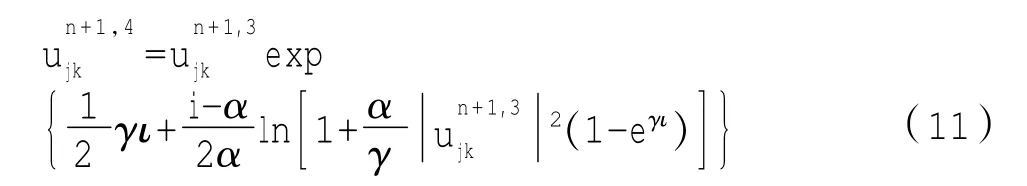
第四步：

第五步：

第六步：

第七步：

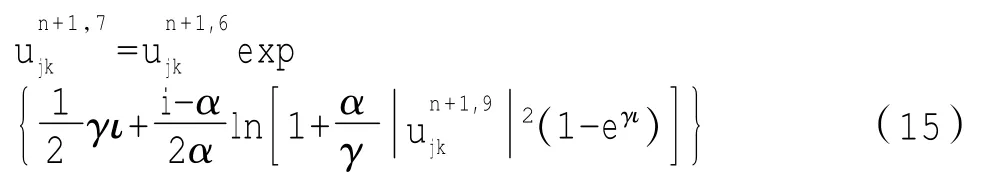
3 数值实验

一般地，对于二维线性方程，分裂步紧差分格式和对应的紧交替隐格式本质是一致的，不一样的只是计算方式，最后达到的预期精度都可在时间上获得四阶精度，空间四阶精度.并且根据文献[2]可知，其收敛性和稳定性都很好，并且分裂步差分可以借鉴对应的交替隐格式来进行分析，并且可以推广到多维线性情况.但是，由于分裂步方法的理论体系还未完全建立，对非线性问题的理论研究还有待深入.

［1］孙志忠.偏微分方程数值解法［M］.北京：科学出版社，2012.

［2］ShanshanWang，LumingZhang.Split-steporthogonal spline collocation methods for nonlinear Sch?dinger equations in one，two and three dimensions［J］. AppliedMathematicsandComputation,2011，（218）: 1903-1916.

［3］MehdiDehghan，Ameneh Taleei.A compact split-step finite difference method for solving the nonlinear Sch?dinger equations with constant and variable coefficients ［J］，Computer Physics Communications，2010,(181):43-51.

（责任编辑 赵巨涛）

O13

A

1673-2015（2015）02-0063-02

2014—11—26

高新忙（1988—）女，山西临汾人，硕士，主要从事偏微分方程的数值解法。