广义倾斜对_参考网

广义倾斜对

2015-07-07廖贻华覃胜喜赵巨涛

长治学院学报 2015年2期

关键词：长治对偶同构

廖贻华，覃胜喜，赵巨涛

（1.广西大学数学与信息科学学院，广西南宁 530004；2.长治学院数学系，山西长治 046011）

广义倾斜对

廖贻华1，覃胜喜1，赵巨涛2

（1.广西大学数学与信息科学学院，广西南宁 530004；2.长治学院数学系，山西长治 046011）

设Λ为交换Artin环R上的一个Artin代数，D是Artin代数对偶，Λ上的广义倾斜对（C，T）引入后，证明了广义倾斜对（C，T）的Artin代数对偶（D（T），D（C）也是广义倾斜对。

Artin代数；广义倾斜对；Artin代数对偶

倾斜理论研究源于20世纪70年代。1979年Auslander、Platzeck和Reiten[1]在构造不可分模时考虑了倾斜模；1980年Brenner和Butler[2]给出倾斜模概念；2001年Miyashita[3]给出了Artin代数上倾斜对的概念,它是倾斜模及余倾斜模的双重推广。2007年，魏加群和惠昌常[4]对倾斜对作了进一步研究，引入广义倾斜（C，T）对的概念，并通过Artin代数对偶函子D来研究广义倾斜对的对偶性质.

1 预备知识

设Λ是Artin R-代数，即交换Artin环R上的一个Artin代数。文章中的模均为有限生成的左Λ-模,用mod Λ表示有限生成的左Λ-模组成的范畴, mod Λop表示有限生成的右Λ-模组成的范畴。并假设范畴是关于同构封闭的Λ-mod的全子范畴，对任意Λ-模M，add M表示同构于M的所有有限直和的直和项组成的子范畴.

设C为mod Λ的子范畴，用C表示mod Λ的子范畴，其对象Λ-模M满足条件：存在一个长度有限的正合列

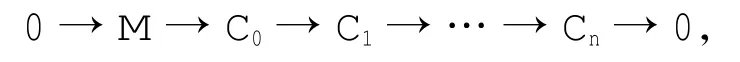
其中Ci∈C，i=1,2,…,n.

对偶地，我们用C表示mod Λ的子范畴,其对象Λ-模M满足下列条件：存在一个长度有限的正合列

其中Ci∈C，i=1,2,…,n.

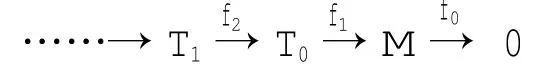
其中Ti∈addT，i=0,1,2…n,Imfi∈T┴。对偶地┴T表示所有满足条件的左Λ-模N组成的范畴，אT表示所有满足下列条件的左Λ-模M组成的┴T的子范畴：存在正合列

其中Ti∈addT，Kerfi∈┴T,i=0,1,2…n,

下面我们引入广义倾斜对的概念。

假定C,T是Artin代数Λ上的模。如果C,T满足以下4个条件:(1)C是自正交的，(2)T是自正交的，(3)T∈Cא,(4)C∈אT，则称模对（C,T）为一个广义倾斜对。注意到Λ上的倾斜对（C,T）是满足下列条件的模对：(1)C是自正交的，(2)T是自正交的，(3)אT，故每个倾斜对（C,T）都是广义倾斜对.

文章中Artin代数对偶HomR（-,E(R/J(R))）记为D，其中J(R)是Λ的中心R的Jacobson根，而E(R/J (R))是R/J(R)的内射包络.

2 主要结果

对于一个给定的广义倾斜对（C,T），为了能获得一个新的广义倾斜对，这里需先给出几个基本结论。

引理1 从modΛ到modΛOP的函子=HomR（-, E(R/J(R))）=D与函子HomΛ（-，D（Λ））同构。

证明见[5,Prop3.5,Chp II].

引理2 如果M∈modΛ是一个自正交模，记Γ＝EndΛ(M)op,则对所有的C∈┴和A∈אM都有同构

Exti（C，A）≅Exti（HomΛ（A，M）,HomΛ（C，M））,i=1,2,…成立.

证明见[6,定理3.2.2,Chp III].

讨论广义倾斜对的对偶性质，获得文章主要结果如下.

定理如果C,T∈mod Λ,且（C,T）为mod Λ中的一个广义倾斜对,则（D（T），D（C））是mod Λop中的一个广义倾斜对.

证明.首先Λ是Artin R-代数，则Λop也是一个Artin R-代数见[5,§2.1,Chp II].下面先证. D(C)∈D(T)א.

由于（C,T）为一个广义倾斜对,故有C∈אT,故存在一个正合列

根据引理 1,函子D≅HomΛ(-,D(Λ)),而D(Λ)是一个有限生成的双边内射余生成子 (参考 [7, §3.2,Chp III]),因此D≅HomΛ(-,D(Λ))是一个反变正合函子.于是用函子D作用于正合列（2.1）得到下列正合列

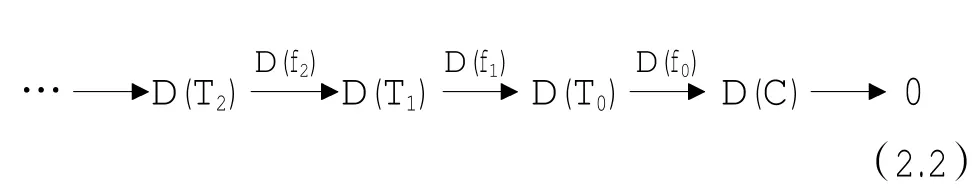
由于Ti∈addT,故有自然数k及模Ti'使得Ti⊕Ti'≅D(Tk),于是有：

因此D(Ti)∈add D(T).

另一方面Kerfi∈┴T,i=0,1,2…n,即有（Kerfi,T）=0.在引理2中取M=D(A)，则有אM=אD(Λ)=mod Λ，┴M=┴D(Λ)=mod Λ，再由引理1可得

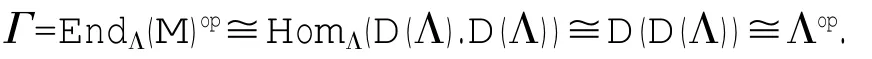
由引理1,对i=0,1,2,…也有j=1,2,…也有

由引理2有

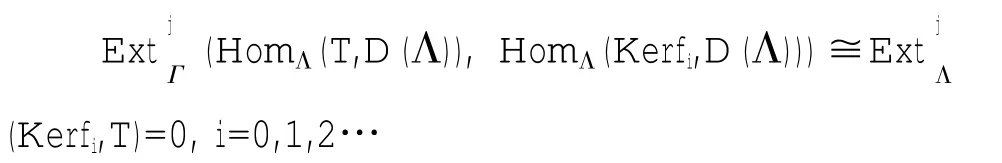
于是对i=0,1,2…,j=1,2,…有

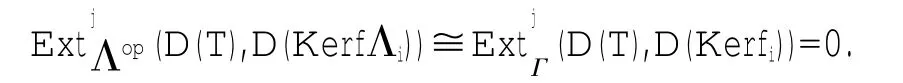
而由D是反变正合函子不难知道D(Kerfi)=ImD(fi)故由上式)可得

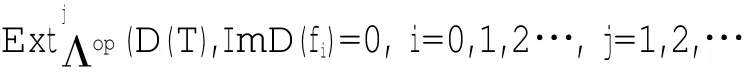
因此ImD(fi)∈D(T)┴.由(2.2)式可知D(C)∈D(T)א.

类似地,由T∈Cא出发也可推导出D(T)∈D(T)א.

余下的工作只需要证明Λop-模D(T)与D(C)都是自正交的.事实上根据引理1与引理2有对j=1, 2,…有

即Λop-模是自正交的，同理可证Λop-模D(C)是自正交的.

因此,modΛop中的模对(D(T),D(C))是一个广义倾斜对.

［1］Auslander M,Platzeck M I,Reiten I.Coxeter functorswithoutdiagrams［J］.Trans.Amer.Math.Soc.1979,250:1-46.

［2］Brenner S,Butler M. Generalizations of the Bernstein-Gelfand-Ponomarev reflection functors［J］.V.Dlab(ed.)P.Gabriel(ed.),Representation Theory II.Proc.ICRA II(Ottawa),Lecture Notes in Math,832,Berlin:Springer-Verglag,1980.103 -169.

［3］Miyashita Y.Tilting modules associated with a series of idempotent ideals［J］.J Algebra,2001,（238）: 485-501.

［4］WeiJia-qun,XiChang-chang.Acharacterization of the tilting pair［J］.J Algebra,2007,（317): 376-391.

［5］Auslander M,Reiten I,Smalo S O.Representation Theory of Artin Algebras［M］.London: Cambridge University Press,1997.

［6］Liao Yi-hua.Tilting Pairs and Approximations［D］.Nanjing:SoutheastUniversity,Doctoral dissertation,2012.

［7］Colby R R,Fuller K R.Equivalence and Duality for Module Categories(with Tilting and Cotilting for Rings)［M］.London:Cambridge Univ.Press, 2004.

Liao Yi-hua1,Qin Sheng-xi1,Zhao Ju-tao2

（1.School of Mathematics and Information Science,Guangxi University,Nanning Guangxi,530004；2.Department of Mathematics,Changzhi University,Changzhi Shanxi,046011）

If Λ was set as an Artin algebra over a commutative Artin ring R,D the Artin algebra duality,and the notions of the generalized tilting pairs(C,T)over an Artin algebra Λ were introduced,it was proved that(D(T),D(C))are generalized tilting pairs provided that(C,T)is a generalized tilting pair.

Artin algebra;generalized tilting pair;Artin algebra duality