反例在可测函数中的应用

张安玲

（长治学院 数学系，山西 长治 046011）

反例在可测函数中的应用

张安玲

（长治学院 数学系，山西 长治 046011）

可测函数中的概念、定理很多，而且各个概念、定理之间的关系非常紧密、复杂，使得学习这部分内容变得更加抽象，难以理解透彻。通过构造和引入反例，可以深入浅出，有效准确地理解可测函数中的一些概念之间的关系，更加重视定理的条件和结论，能够进一步深入理解和掌握所学知识点。

反例；可测函数；收敛

在数学分析课程中，所研究的函数基本上是连续函数，许多情形还要求是可导的.实变函数论所研究的是可测函数，可测函数是从测度的观点来研究函数[1]，它包含很多不连续的函数，可测函数比连续函数宽泛的多.

反例是数学中一种重要的思维方式，它是用来说明某个命题不成立的例子.恰当的运用反例可以换一个角度抓住概念的本质，从而更好的理解知识[2].

理解可测函数对于全面掌握实变函数是至关重要的.而可测函数与连续函数之间的关系，叶果洛夫定理、鲁津定理、勒贝格定理的条件与结论，处处收敛、几乎处处收敛、一致收敛、依测度收敛之间的关系等都是可测函数这部分内容的重点，它们之间的关系非常复杂.在学习过程中，用恰当的反例可以有效的说明这几种收敛之间的关系.另外，反例也可用来强调使用定理的条件.因此利用反例不仅可以进一步纠正某些错误的认识，也能引起对条件和结论的重视.

1 可测函数

1.1 非可测的函数

定义[1]设f(x)是定义在可测集E⊆Rn的实函数.如果对于任何有限实数a，E[f＞a]都是可测集，则称f(x)为定义在E上的可测函数.

我们知道，许多函数都是可测函数，可测函数是连续函数的推广，但是，并不是所有的函数都是可测函数.

例 取Rn中的一个不可测集E，则E的特征函数为Rn上的不可测函数。

注：上例中的特征函数XE(x)并不是一个简单函数，因为E是不可测集.从而不能按照简单函数是可测函数的方法判断该函数可测.

（2）可测函数与连续函数的关系

我们知道，定义在可测集E⊂Rn的连续函数都是可测函数，反之成立吗？通过引入反例来说明.

例 著名的Dirichlet函数[3]，

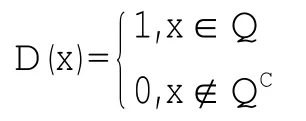
分析：对任意有限实数a，

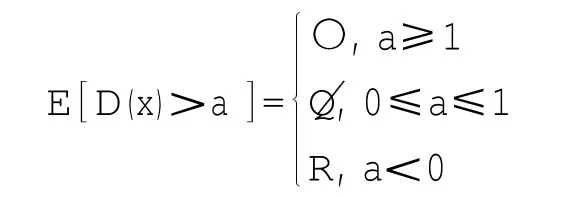
故Dx是可测函数.但是Dirichlet函数是典型的不连续函数.从而得到可测函数不一定是连续函数.

还有在[0,1)上的黎曼函数，

它也是一个典型的可测非连续函数.

（3）绝对值可测与函数可测的关系

若f(x)是可测，则|f(x)|也可测；但反之若|f(x)|可测，f(x)不一定可测.

例 设E为[0,1]上的可测集，令

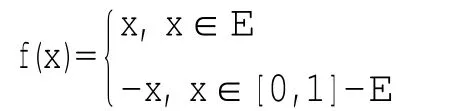
显然|f(x)|=x，而|f(x)|在[0,1]上是连续函数，故|f (x)|在[0,1]上勒贝格可测，但f(x)在[0,1]上非可测.

所以f(x)在[0，1]上不可测.

（4）可测函数的运算

若f(x)，g(x)在E上可测，则f(x)+g(x)，f(x)g(x)均在E上可测.但反之不真.

例在Rn中取不可测集E，令

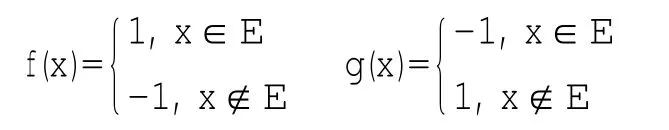
f(x)+g(x)=0,f(x)g(x)=-1,x∈Rn.显然f(x)+g(x),f(x)g(x)都是R上的连续函数，所以可测.而f(x)，g(x),均为Rn上的不可测函数.

（5）对任意实数a，集合E f=a[ ]恒可测，但f(x)不一定可测.

若f(x)在E上是可测函数，则对任意实数a，集合E f=a[ ]都是可测集，但反之不真。即对任意实数a，集合E f=a[ ]恒可测，但f(x)不一定可测。

例 在(0,+∞)中取不可测集A，在R1上定义

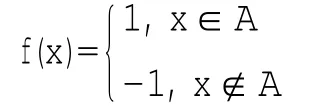
则∀x∈R1，集合R1[f=a]至多包含两点，从而为有限集，所以是可测集.但因为集合R1[f＞0]I(0,+∞)不可测，所以f(x)为不可测函数.

（6）连续函数与可测函数的复合函数未必可测

若f(x)是R1上的可测函数，g(x)为R1上的连续函数，则复合函数g(f(x))是可测函数.但是，复合函数f(g(x))未必是可测函数，从而两个可测函数的复合函数不一定是可测函数[4].

例 设φ为[0,1]上的Cantor函数，其中φ的定义如下[4]：

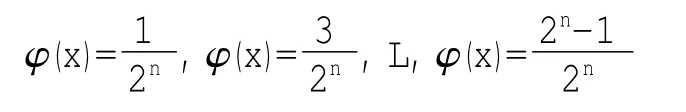
于是φ在[0,1]中的Cantor余集上有了定义，它在这上面是单调不减的.

在Cantor集上给φ补充定义，先令 φ(0)=0，对于其他x∈C，其中C为Cantor集，令

φ在[0,1]上单调不减，并且它在[0,1]上连续.

则h(x):[0,1]→[0,1]为严格递增的连续函数，取W⊂h (C)为不可测集，则M=h-1(W)⊂C可测，使h(M)=W不可测.令g(x)=h-1(x)，从而M=g(W)可测，则g(x)连续且严格递增.令f(x)为M的特征函数，则f(x)为可测函数.记E=[0,1]，则由不可测，知f(g(x))为不可测函数.

2 叶果洛夫定理

（1）叶果洛夫定理中，m(E)＜∞的条件不可少

该定理表明，凡是满足定理假设的几乎处处收敛的可测函数列，即使不一致收敛，也是“基本上”一致收敛的.

注：此定理中，m(E)＜∞的条件不可少.

例 取E=(0,+∞)，则m(E)=∞.作E上的函数列：

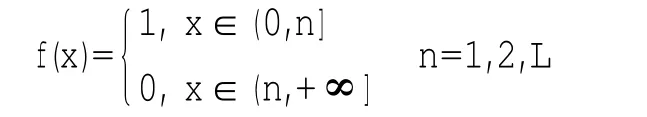
（2）叶果洛夫定理的结论不能加强为m(EEδ)=0

叶果洛夫定理中，对任意δ＞0，存在子集Eδ⊂E，使｝在Eδ上一致收敛，且m(EEδ)＜δ。其中m (EEδ)＜δ不能改为m(EEδ)=0.

例 设E=(0,1)，在E上定义

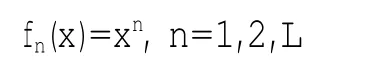
3 几乎处处收敛但不依测度收敛的可测函数列

定理（勒贝格Lebesgue）设

（1）mE＜∞；

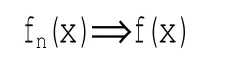
该定理表明，在mE＜∞这个条件下，几乎处处收敛的几乎处处有限可测函数列是依测度收敛的.当mE=∞时，这种蕴含关系就不成立.

例取E=(0,+∞］，则mE=∞.作E上的函数列：

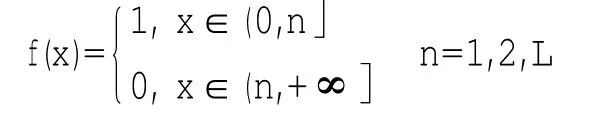
4 结论

通过引入反例，可测函数中诸多复杂关系得以明晰化，几种收敛的互相蕴含关系更明朗化，对叶果洛夫定理、勒贝格定理的条件和结论加深了印象.恰当引用反例，对理解可测函数这部分内容起到了事半功倍的效果.

［1］程其襄,张奠宙,魏国强,等.实变函数与泛函分析基础［M］.北京：高等教育出版,2010.

［2］刘京鑫.反例在实变函数中的运用［J］.高等数学研究,2009,12(4):117-121.

［3］李景廉.函数在实变函数中的应用［J］.佛山科学技术学院学报,1999,17(3):67-70.

［4］程庆,冯远征.实变函数中的反例［M］.郑州:河南大学出版社,1989.

Zhang An-ling

（Department of Mathematics,Changzhi University,Changzhi Shanxi 046011）

There are a lot of concepts,theorems in measurable function,and the relationship between each concept,theorem is very close and complex.So this section becomes more abstract and difficult to understand.By constructing and introducing counterexamples,the relations between some concepts in the measurable function can be easily understood,and the conditions and conclusion of theorem are more valued.As a result,the learned knowledge can be further mastered.

counterexample;measurable function;convergence

O174.1

A

1673-2015（2015）02-0060-03

（责任编辑 赵巨涛）

山西省高等学校科技项目(2013158)。

2014—11—06

张安玲（1980—）女，山西长子人，讲师，硕士，主要从事最优化理论与方法，智能优化算法方向研究。