微型电动车车架结构优化设计与分析

2015-07-07于玉真李志斌董小雷邓程程

制造业自动化 2015年2期

于玉真，李志斌，董小雷，邓程程

（河北联合大学机械工程学院，唐山 063009）

0 引言

车架作为车辆的承载基体，直接或间接的承受着来自车架附件、乘客及路面的载荷和激励。为了使车架拥有良好的操控平顺性，稳定性等力学性能必须使车架有足够的静强度和良好的动态指标。在对车架的性能进行分析前，通常是在三维软件中通过参考现有模型或进行自行设计来对车架进行直接建模。现基于Workbench中的shape optimization模块，采用拓扑优化法，只需建立车架的“毛坯”模型，经过材料去除便可得到车架的参考模型进而进一步搭建理想模型，同时为二次轻量化建模准备基体。减轻车辆自身质量，不仅节约了原材料，降低汽车的生产成本，而且也降低了能源消耗[1]，有利于环保并提高了车辆的续航里程。而且汽车自身质量每降低1%，便可节省燃料消耗0.6%~1.0%[2]。

1 拓扑优化建模

四排微型旅游观光电动车车身初始模型如图1所示。整体设计尺寸为4000×1300×1400mm。

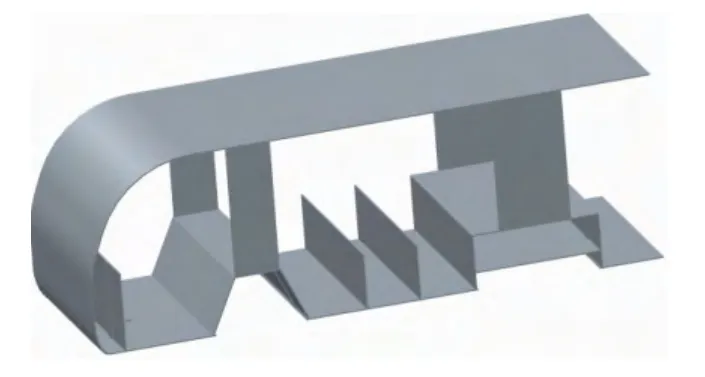
图1 车架初始模型

1.1 优化初始模型

拓扑优化方法在概念设计阶段为设计者提供科学依据,使复杂的结构或部件可以灵活、理性地进行优选，以获得最佳效果[3]。它可以在均匀分布材料的设计空间内找到最优的材料分布方案，该方案在拓扑优化中表现为“最大刚度”设计。拓扑优化属于结构优化的一种，其目的是找到材料的最大利用率，尽可能寻找可以对整体结构的强度不产生负面影响的可去除面积，优化材料的分布使其在确定的负载下获得最大刚度，进而去除材料[4]。拓扑优化是寻求目标函数在所给定的约束条件下达到极值状态，定义设计变量ηi为单元i的虚构材料密度，取值范围为0~1。当 ηi≈0时表示该单元的材料将被移除，当 ηi≈1则表示该单元的材料将被保留。

电动车在行驶过程中有多种工况如满载弯曲工况、扭转工况、刹车及转弯工况等，现以最严重的扭转工况（对角两轮不着地）为分析背景对模型进行加载，以得到最可靠的材料分布方案。释放左前轮和右后轮板簧悬挂点的由度，另外两个板簧悬挂点做固定约束，在设计的乘客、电池、附件等位置施加相应载荷，并对车架整体施加竖直向下的标准重力加速度。由于车辆在路面行驶时会产生对称或非对称的动载荷，受其作用车架会产生更大变形，所以各载荷通过乘以动载系数来考虑动载的影响。

动载系数取决于三个因素：道路条件、汽车行驶状况和汽车的结构参数。动载系数的计算公式为：

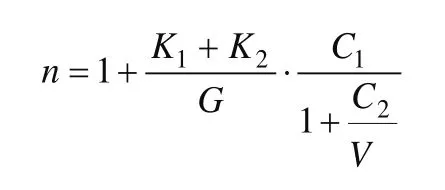
式中：

K1为前轮弹簧系统的刚度；

K2为后轮弹簧系统的刚度；

G为满载时总重量；

C1为道路常数，一般C1取80mm～100mm；

C2为经验系数,一般取1000Km/h2；

V为最高车速，km/h。

取K1，K2为418[5]，经计算得n为1.4。考虑实际满载扭转工况下的整体的柔度，将其作为目标函数，定义体积约束为拓扑约束参数[6]，设置目标缩减量为70%。

初步优化结果如图2所示。深色部分为材料去除区域，由于是对角扭转工况，所以在参考优化结果建模时应取一侧预留材料较多部分镜像至另一侧。

图2 拓扑优化结果

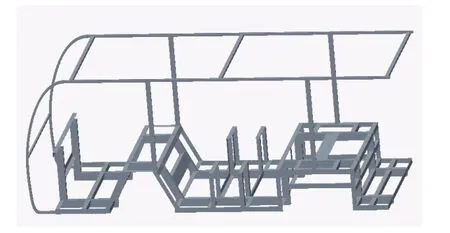
图3 车架模型

用Creo2.0参考优化结果建立初始模型，车架材料为Q345，主要采用标准的矩形钢80×40×2.5、角钢50×50×3.0等型材焊接而成，车架重157.4kg，如图3所示。

为了验证优化结果的可参考性及车架模型的强度是否合格，对模型进行强度分析，现以最危险的对角扭转工况为例对其进行分析。加载与约束方式与拓扑优化过程相同，分析结果如图4、图5所示。

图4 车架位移云图

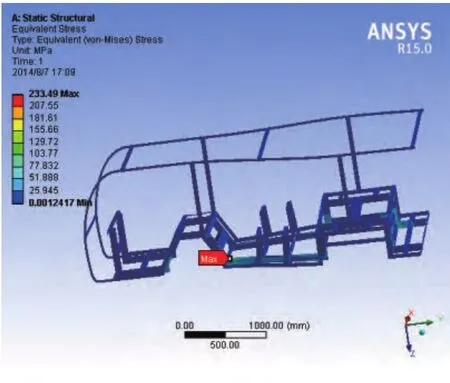
图5 车架应力云图

最大位移发生在车架尾部拐角处，变形量为6.34mm，最大应力发生在中部纵梁与第一排座位的斜纵梁连接处，最大应力为233.49MPa，为集中应力，小于屈服极限。可见通过拓扑优化得到的模型有较好的参考性，模型强度满足条件。

1.2 模型的轻量化

在第一次建模的基础上行进材料去除，以减小模型的质量，获得最优的模型结构。类似于首次优化的方法得到可去除材料区域，由于模型已经是梁架结构可去除材料的区域不多，所以需要更细腻的网格来支持二次优化。经过网格划分，结果有260894个单元，900283个节点。设置目标缩减量为15%，得到的优化结果如图6所示。

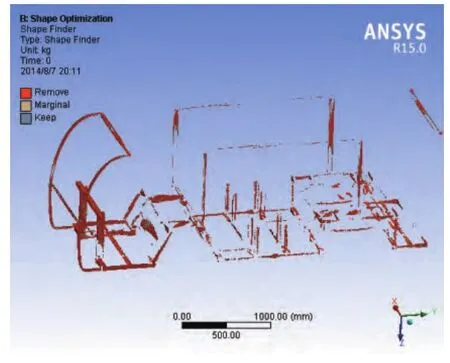
图6 材料去除区域

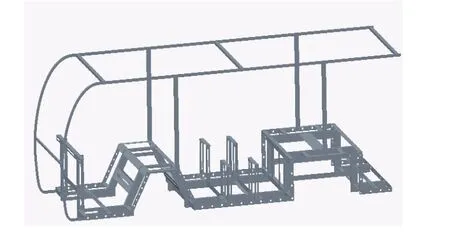
图7 轻量化车架

由图6可知，车架顶棚及车架前部悬挂附件处移除材料较多。由于所选材料的厚度较薄，所以不再考虑材料厚度的优化。通过对各部分局部放大研究及结合实际情况得到车架的轻量化方案：1）车架顶棚及支架基本不参与承载及支撑，所以将其材料改为铝合金。2）在该车架前部、前排座位防扭梁、中间座位支撑角钢、后部脚踏板等处开以直径为12mm、27mm、16mm（参考铣刀或钻头的直径）的半圆为端部的长孔。3）车架周围的薄钢板主要用于车架蒙皮时折边参照，不参与受力，将其上打直径为22mm的圆孔。二次轻量化后的模型如图7所示。经有限元分析车架的变形、应力如图8、图9所示。

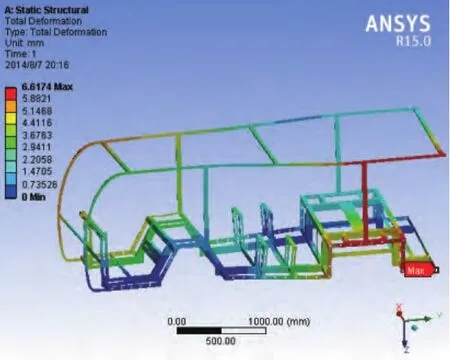
图8 优化后车架位移云图

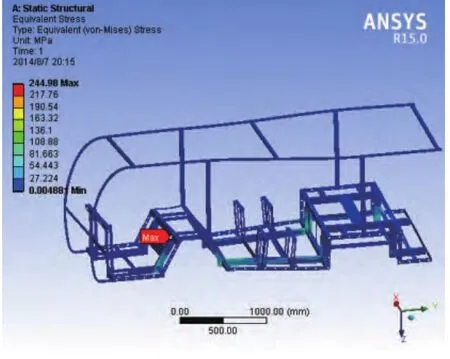
图9 优化后车架应力云图

优化后车架最大位移为6.62mm，位置不变，大小增加0.28mm，最大应力为244.98MPa，为集中应力，发生在第一排座位的斜纵梁与左边横梁的接触处，应力增加11.49MPa。质量为137kg，减小了19.6kg，减轻12.45%。

在原始模型的基础上，通过拓扑优化进行了材料的最优分布，使得车架拥有更好的强度结构，节约了钢材成本，减轻车身质量[7]；在最危险工况下对车架结构进行了强度校核，其结果满足设计要求。

2 模态分析

车架不仅要满足静态强度，还须有良好的动态指标。而模态分析作为衡量模型动态特性的重要方法。它克服了静态方法的局限性，强调从结构的整体考虑问题，在性能校核中考虑了振动的因素，合理的振动特性也是十分重要的[8]。所以，为提高车辆行驶的安全性、舒适性和可靠性，还必须对车架结构进行模态分析。然而模态又分为自由模态和约束模态，需要求解自由模态还是约束模态，完全取决于工作的需要，模态分析时的约束方式应与实际工作条件下一致，如果工作时结构没有约束，如飞机、火箭等，则需要进行自由模态分析[9]。虽然模拟时很难达到现实中的边界条件，但是尽可能靠近真实的工作状态还是具有一定指导意义的。如减振系统可能对模型的振型有一定程度的影响，所以在模拟满载弯曲工况的振动特性时，要同时考虑减振板簧的影响，车架的力学模型如图10所示。现只分析满载弯曲工况下电动车的各阶频率，其他工况随机出现且时间短暂，不足以造成共振现象。对骑马螺栓附近的底层板簧做固定约束，吊耳、板簧与销钉之间为销连接，其他载荷与约束与静态分析一致。

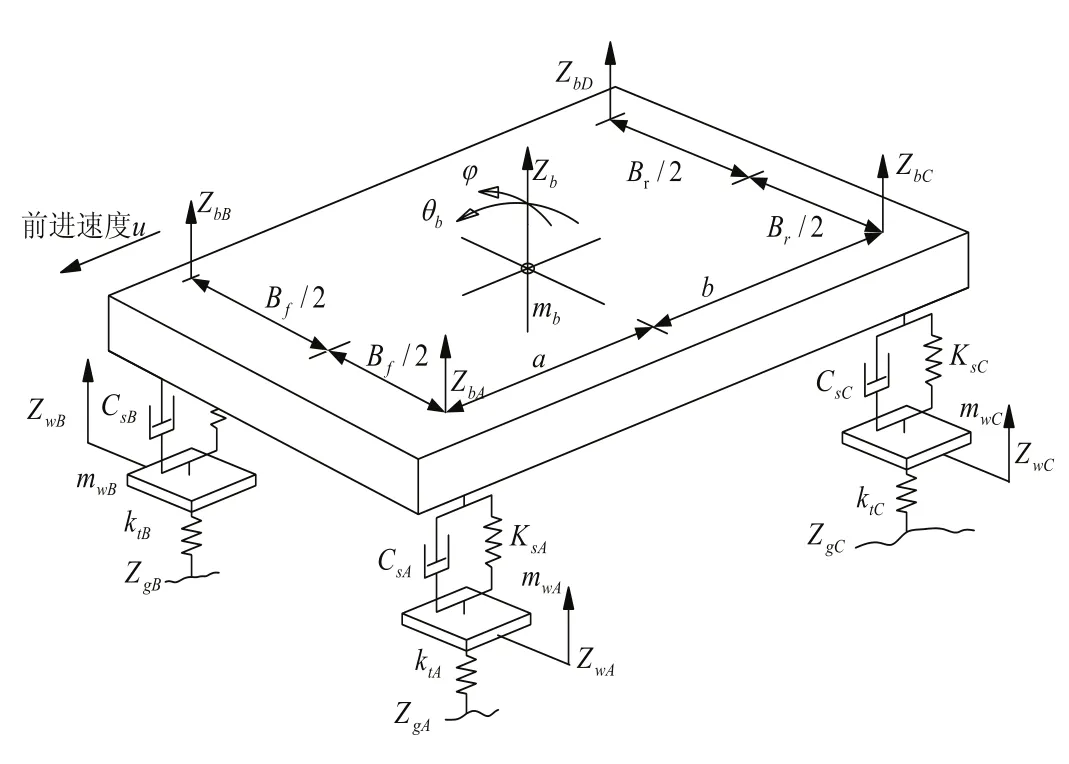
图10 车架力学模型

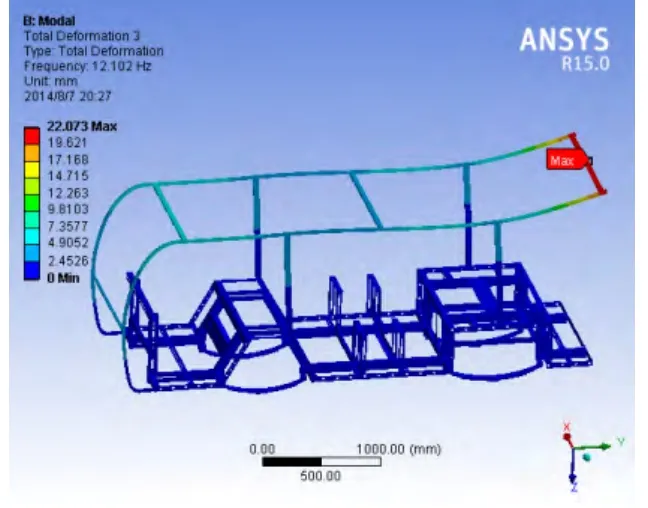
图11 三阶模态振型

通过模态分析，提取车架前8阶频率，各阶频率及振型如表1所示。

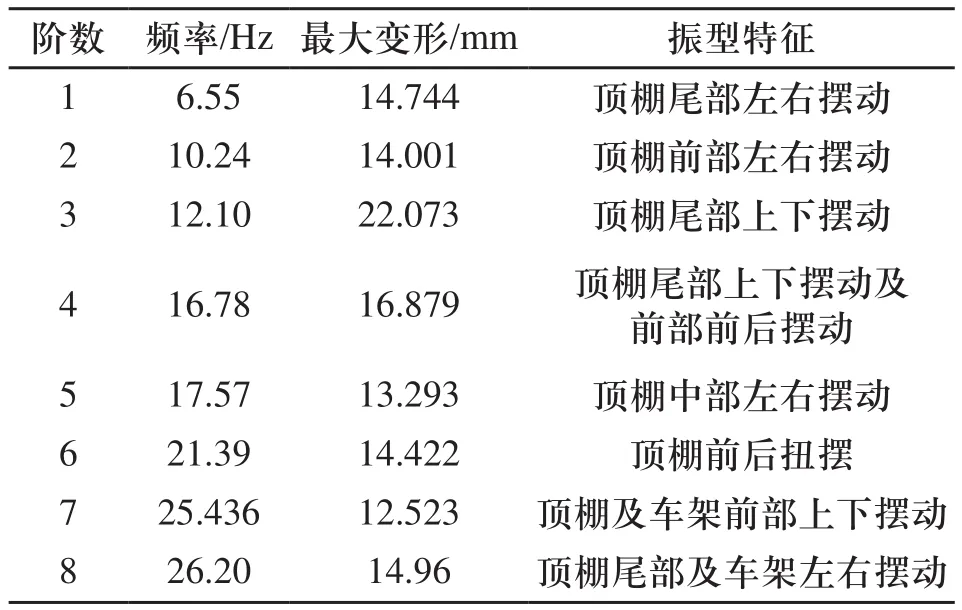
表1 车架各阶频率及振型

由于微型电动车的激振源主要来源于道路的路况，而典型路面实测功率谱密度的的频率主要在Ω=0.1～2次/m的范围内[10]，微型观光电动车的最高行驶速度为50km/h，即14m/s，平时行驶速度在7m/s左右。则输入时间频率f=VΩ，结果大多小于14Hz，主要为前3阶振型。最大变形发生在三阶振型下，顶棚尾部上下摆动，最大位移为2.2cm，如图11所示。另外，从车架的前8阶振型可以看出，各阶振型主要发生在车架顶棚上，并没有影响到底盘结构的安全性。