四旋翼姿态解算算法的对比与研究

王晓初，卢 琛

（广东工业大学 机电工程学院，广州 510006）

0 引言

在捷联式惯性导航中，飞行器的姿态是机体坐标系相对于导航坐标系决定的，而描述这种坐标系的关系可以分为三类，有三参数法、四参数法和九参数法。其中三参数法也叫欧拉角法，四参数法有四元数，九参数法为方向余弦[4]。

利用惯性元件，对飞行器的姿态的解算，是捷联式惯性导航的关键。文献[6]从信号的频域出发，给出了基于互补滤波器的解算算法。文献[2]结合卡尔曼滤波器，给出了基于状态空间的最优解算法。文献[7]采用梯度下降为修正准则，给出了偏差沿梯度负方向修正算法。文献[5]则结合梯度下降与互补滤波器，吸收了各自的优点。本文针对这几种常见的姿态解算算法，从设计准则与实际应用出发，对比分析了各自算法的特点与相似之处。

1 姿态的更新算法

姿态的更新常采用如下流程，将角速度向量[ω]带入四元数微分方程并求解，即可更新四元数[q]。

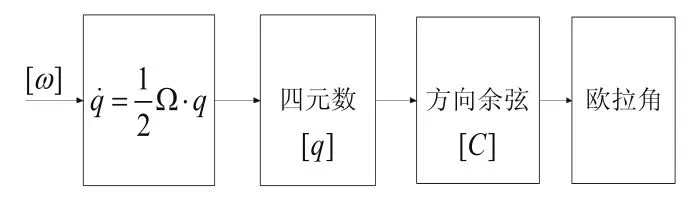
图1 姿态解算流程

四元数微分方程为：

其中，四元数q定义为：q=q0+q1i+q2j+q3k。

写成矩阵形式为：

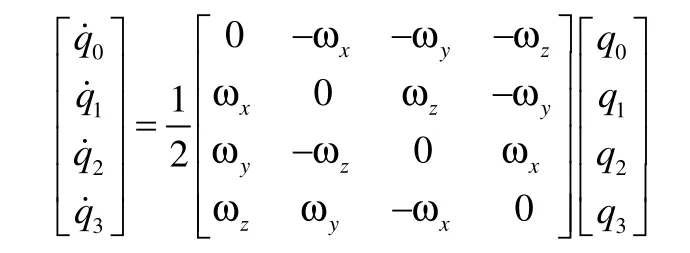
用角增量算法求解微分方程迭代格式为：

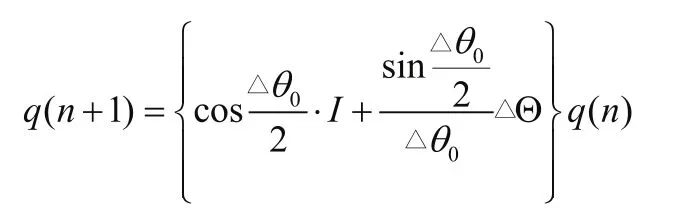
其中：

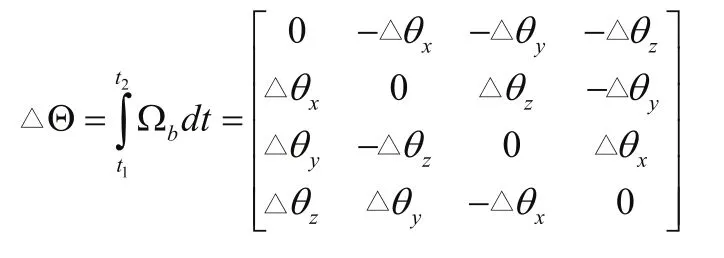
将cos和sin泰勒展开，取一阶近似有：

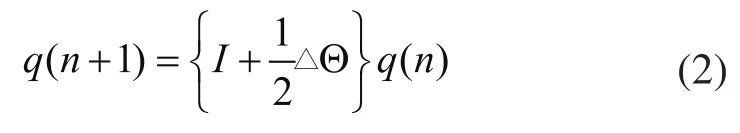
采用式(2)即可更新四元数，但是直接使用四元数不利于PID控制，还需利用方向余弦矩阵[C]将四元数转变为欧拉角。

方向余弦矩阵也称作坐标变换矩阵，是导航坐标系[Xn]到运载体坐标系[Xb]的变换矩阵，有并且方向余弦有两种表示方法，分别为为四元数表出和欧拉角表出，并且两种表出矩阵在同一坐标系下是等价的[1]。

四元数表示方向余弦为[1]：

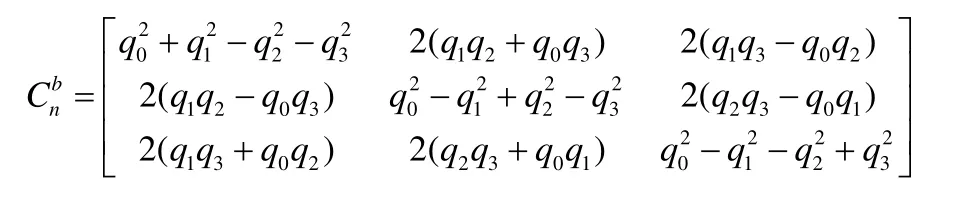
另外，欧拉角表出方向余弦为[1]：

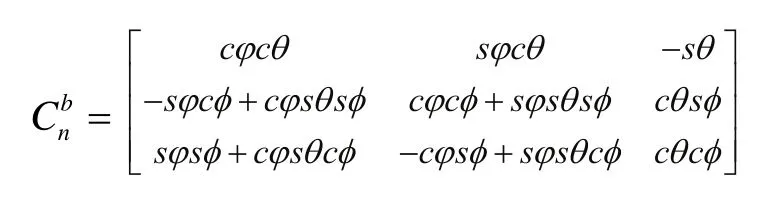
其中c和s分别代表cos和sin，ϕ、θ和φ分别代表欧拉角中的航向角，俯仰角和横滚角[1]。如果已知方向余弦，可以由下列公式求得对应的欧拉角：

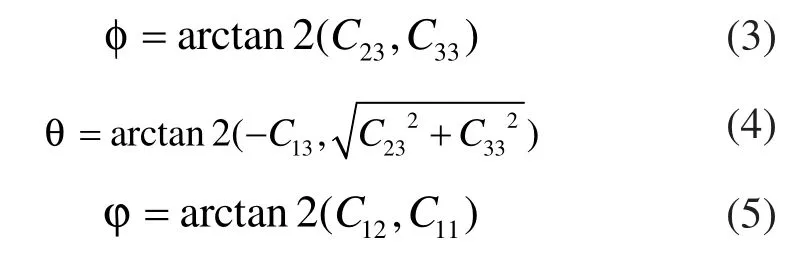
如图1所示，式（2）给出了四元数法的更新迭代格式，更新四元数后即可求得方向余弦，由式（3）～式（5）便可求得到更新之后的欧拉角。

但是整个过程是建立在对角速度的积分，由于字长丢失精度会导致积分误差，且误差会随着时间的延长而加大。所以需要组合加速度传感器来修正姿态矩阵，使误差项逐步减小，最终消除。常用的组合算法有互补滤波算法、梯度下降算法和卡尔曼滤波算法等。

2 常见组合算法的特点

姿态解算算法可以用图2表示，其中由式（2）更新的姿态为qg，它是整个姿态估计q的基础。

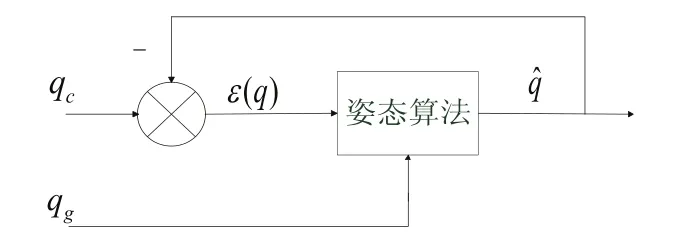
图2 姿态解算算法流程

因为积分误差的存在，所以需结合加速度计的输出qc构成修正偏差ε(q)，然后以不同的设计准则构成算法修正qg，即可得到在特定评判标准下的最优估计姿态q。

2.1 以高通和低通滤波器为修正算法

陀螺仪动态响应特性好，但会产生积分误差。加速度传感器测量姿态没有积分误差，但是动态响应较差。它们在频域上的特性形成互补，从而提高测量精度和系统的动态性能[3]。

如图3所示[6]，表示互补滤波器的输出姿态矩阵，代表载体坐标下的测量加速度单位向量，代表在惯性坐标系下的重力场向量，设。

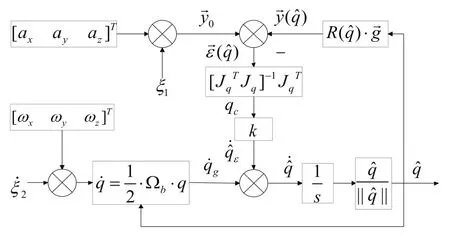
图3 互补滤波器模型

其中误差向量定义为：

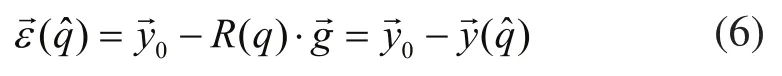
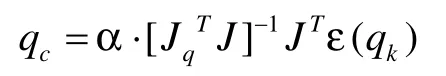
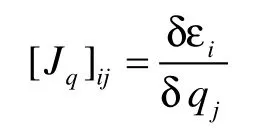
则整个互补滤波器的估计输出为：

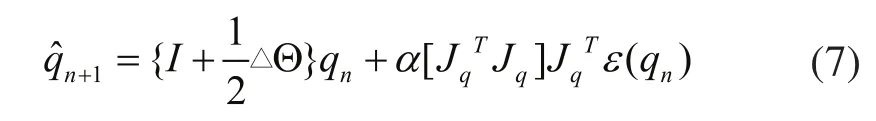
如图3所示，令ξ1为加速度计测量噪声，为陀螺仪测量噪声，则噪声传递函数为：

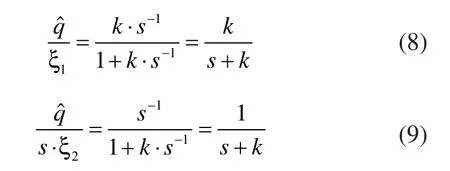
式（8）和式（9）可以用来设计k的取值，从而确定互补滤波器的截止频率在大于fτ的高频段，陀螺仪对解算起主要作用，反之，加速度对解算起主要作用[3]。

2.2 以偏差函数梯度负方向为修正准则

使用式（6）为目标函数，则有梯度：

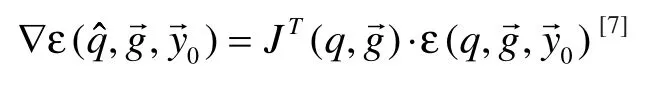
这样就可以通过下列公式进行修正：

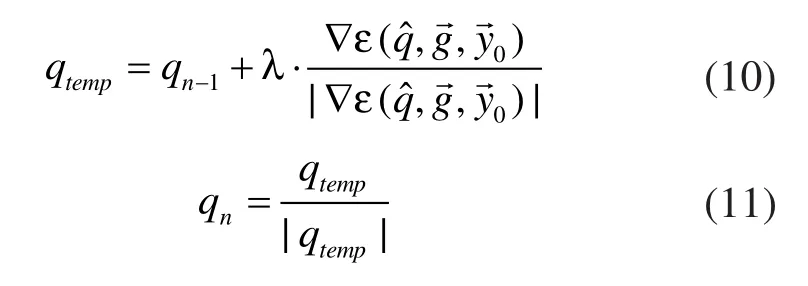
式（10）、式（11）即为梯度下降迭代格式，其中步长λ用来限制偏差收敛速度，但过大的步长可能会导致估计不准确[5]。

2.3 以卡尔曼滤波器为基础的修正算法

卡尔曼滤波器以状态空间为基础，把信号过程看做在白噪声作用下的线性输出[5]，

算法表述为：最优值=预测值+kg.修正量，其中kg为动态调整增益。

考虑如下线性系统离散模型：

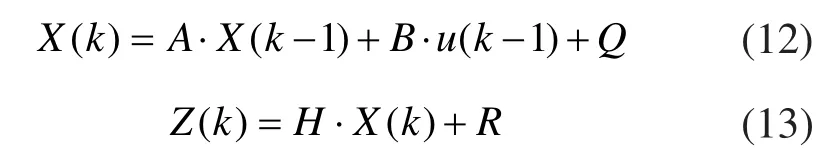
其中X(k)是系统的状态向量，A是状态转移矩阵，B是控制输入矩阵，u(k-1)是控制输入向量，Q是过程噪声协方差矩阵，Z(k)是系统的观测向量，H是观测向量，R是观测噪声协方差矩阵。

使用陀螺仪数据qg和ε(q)建立时间传递模型如下：

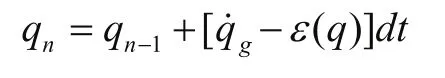
取：

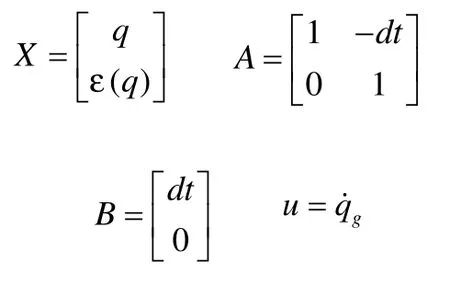
可以得到状态矩阵方程[2]：

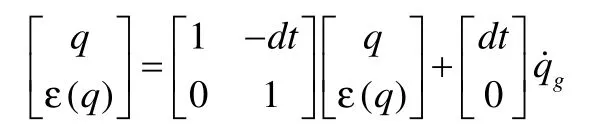
则卡尔曼滤波算法实现步骤为：

根据时间传递方程（12）预测k时刻的输出：

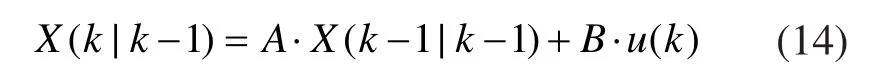
其中X(k- 1 |k- 1 )为上一时刻的最优输出。

计算k时刻预测输出协方差矩阵：

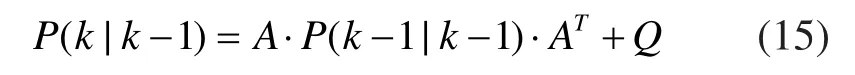
更新k时刻修正增益矩阵：

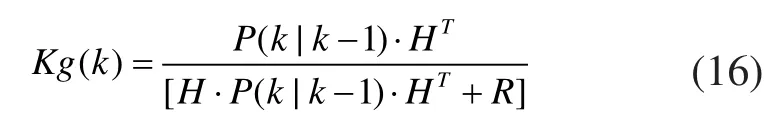
根据观测方程（13）修正预测矩阵：

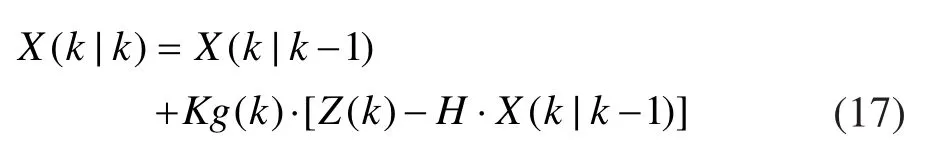
更新最优预测输出的协方差矩阵：

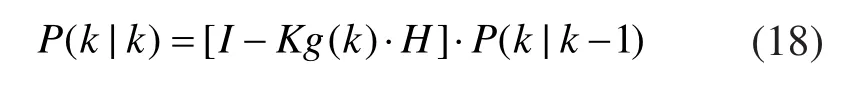
3 实验分析

互补滤波最为简单，基于高通与低通滤波器，构成设计准则来修正姿态；梯度下降则以偏差函数的负梯度为校正准则，使其以最快下降方向进行校正；卡尔曼滤波以状态空间为基础，从时间传递方程和测量方程出发，得出考虑各种随机误差在内的最佳线性估计，如图4所示，为实时角度采样输出。

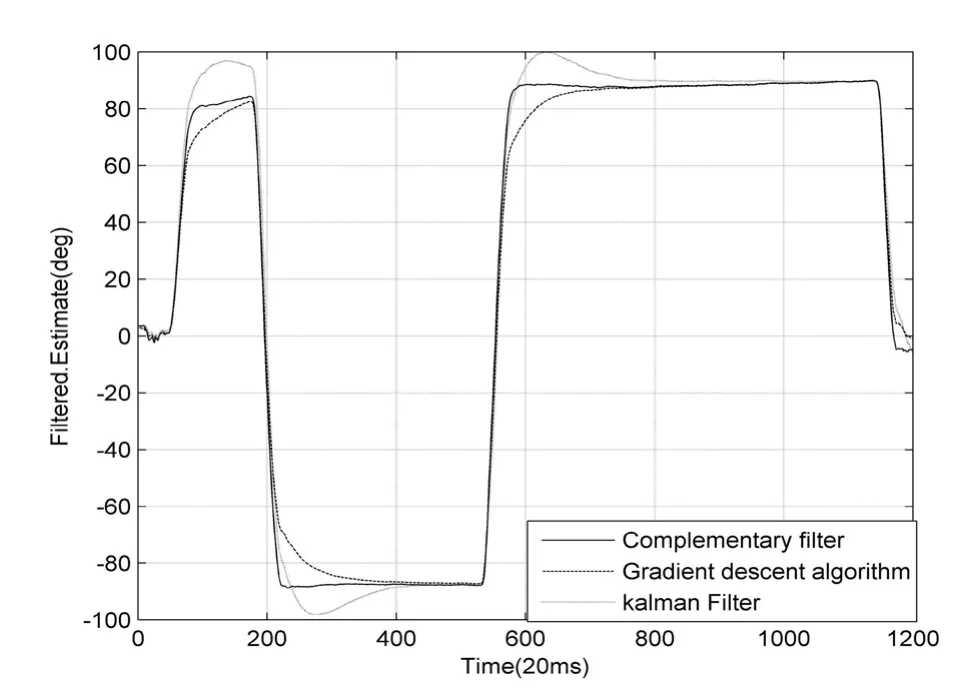
图4 三种算法输出对比

从图中可以看到，当姿态在迅速变化时，三种算法的估计输出几乎重叠在一起，此时陀螺仪对姿态更新起主导作用，加速度的修正效果可以忽略。在姿态变化较为平缓阶段，三种算法对姿态修正的差异才凸显出来，这也体现了在不同修正准则下的输出差异，但最终估计输出都会收敛于某一稳定值。

[1]高钟毓.惯性导航系统技术[M].北京:清华大学出版社,2012.

[2]王帅,魏国.卡尔曼滤波在四旋翼飞行器姿态测量中的应用[J].兵工自动化,2011,01:73-74,80.

[3]梁延德,程敏,何福本,李航.基于互补滤波器的四旋翼飞行器姿态解算[J].传感器与微系统,2011,11:56-58,61.

[4]胡庆.基于STM32单片机的无人机飞行控制系统设计[D].南京航空航天大学,2012.

[5]谭广超.四旋翼飞行器姿态控制系统的设计与实现[D].大连理工大学,2013.

[6]Bachmann, E.R., et al.“Orientation tracking for humans and robots using inertial sensors.” Computational Intelligence in Robotics and Automation, 1999.CIRA’99.Proceedings.1999 IEEE International Symposium on.IEEE,1999.

[7]Madgwick,Sebastian OH,Andrew JL Harrison, and Ravi Vaidyanathan.“Estimation of IMU and MARG orientation using a gradient descent algorithm.”Rehabilitation Robotics (ICORR), 2011 IEEE International Conference on.IEEE, 2011.

[8]Fresk, Emil,and George Nikolakopoulos.“Full quaternion based attitude control for a quadrotor.” Control Conference (ECC),2013 European.IEEE,2013.