超高稳态加速度承载条件下转子部件结构可靠性研究

李晓杰，王成林，贾美慧

（北京物资学院，北京 101149）

0 引言

随着航天、航空、生物、分析化学、高速加工等领域的迅速发展，机械装置越来越多的在高加速度承载条件下运行，由于组成部件在承受高加速度载荷作用下其应力、应变、温度、振动等方面特征改变，会导致组成部件功能失效，进而引发产品整体失去工作能力，因此目前对于产品在高加速度加载条件下使用特性分析和测试就尤为重要[1]。目前利用高速旋转产生向心加速度进行加速度承载实验是目前具备较强应用前景的新型实验方法。其基本实验原理及转子部件模型俯视图如图1所示。

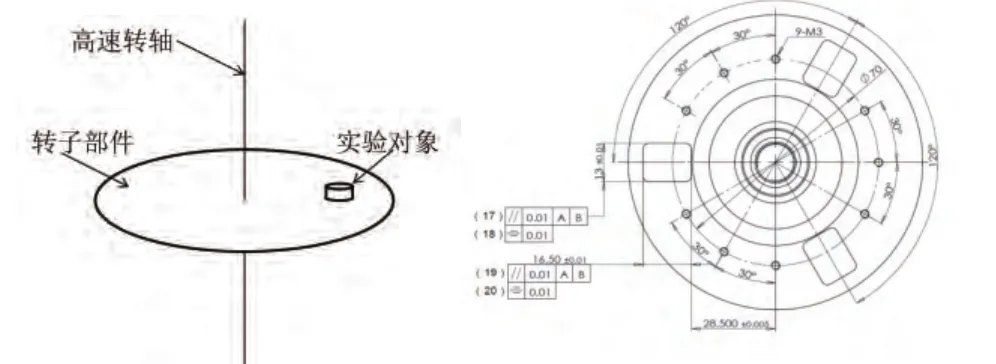
图1 高加速度实验系统原理简图及模型俯视图

目前国内外根据不同的使用要求相继研发了相关的实验装备，并已经在航天、生物等领域进行了广泛的应用，针对此类设备的主要研究内容为：转子系统的临界转速和稳态、瞬态响应计算；关于转子系统运动稳定性的研究；转子系统的优化设计和转子的动平衡技术；轴承的动力特性；转子系统的故障诊断；转子的振动主控制；非线性转子动力学等；转子-轴承系统可靠性[2]。

综合考虑目前的研究成果可知研究的重点侧重整个旋转传动轴系的动态特性，对转子部件本身的研究往往需要做出若干的简化和假定，一般是简化为具有一定质量、刚度、阻尼特征值的刚体，忽略了转子部件本身的研究[3]，尤其制造过程中形成的系统静态误差在工况参数影响下演变为系统动态误差，并对系统运行产生影响，特别是对具有精密配合关系、受到强应力作用、产生较大应变的转子部件的动态特性影响更为显著，而目前此类研究还未深入开展。

本文对超高稳态加速度承载条件下转子实验设备的安装孔结构，建立力学模型，综合评价误差对转子部件结构可靠性的影响。

1 转子部件建模与结构力学特性分析

根据公式 a =ω2·r可知，转子部件的角速度值和回转半径共同决定了该设备的加速度应力场的强度。因此实验对象的径向变形具有非线性分布的特征，同时限元方法可以较精准的实现该问题的计算，因此本文将利用ANSYS建立转子部件的三维实体计算模型，对其进行数值求解。根据已构建转子部件模型，进行ANSYS建模，工作转速为6303rad/s，转子部件材料设定为TC4，转子直径设定为100mm，实验对象安装位置回转半径为35mm。在仅考虑离心场力载荷的情况下，简化其受力模型，进行有限元模拟计算，转子部件变形云图如图2所示。

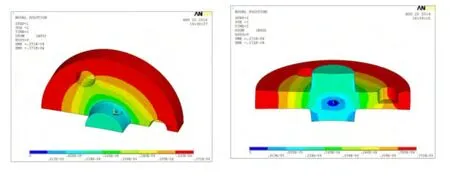
图2 未集成装配关系的转子部件综合变形云图

此时加速度载荷值为1.53×106g（重力加速度值为g=9.8m/t2），转子部件安装孔处径向最大变形量达到了0.082mm，安装孔自下而上孔径逐渐增大；接触应力极值达到360MPa，小于设定材料的许用应力极值830MPa。

本文设定实验对象材料为60SI2MnA钢，其中心位置距回转中心距离为35mm，实验对象的直径为12mm，高度为10mm，约束方式为径向外侧线约束。在仅考虑离心场力载荷的情况下，简化其受力模型，进行有限元模拟计算，应力云图如图3所示。

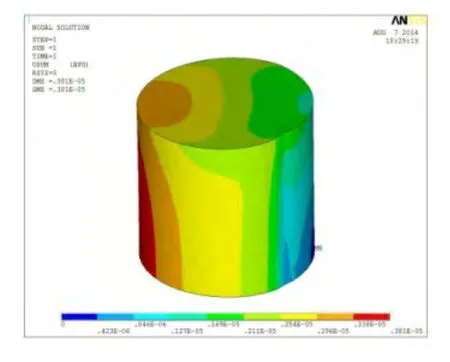
图3 未集成装配关系的实验对象计算结果图（外侧半侧面径向约束）

根据计算结果径向最大变形量达到了0.0839mm，接触应力为890MPa，低于设定材料的许用应力极值1200MPa。对比实验对象及转子部件安装孔结构变形量可知，在工作状态下试验对象径向外侧趋于的径向变形大于对应的实验托盘安装孔处的变形。

根据研究成果得，小间隙配合为相对过渡和过盈配合效果更好的一种配合方式[4]。此时，实验对象在工作状态下径向外侧区域的变形量大于其对应的转子部件安装孔的径向变形，二者之间的接触条件也由线接触过渡为面接触配合。由于小角度斜面的存在会造成ANSYS计算结果出现较大误差，因此将上图案例模型进行适当简化，从影响转子部件应力与变形这两项指标进行分析，建立具有集成装配关系的转子部件有限元计算模型，当间隙量取0.01mm时，转子部件变形云图如图4所示。

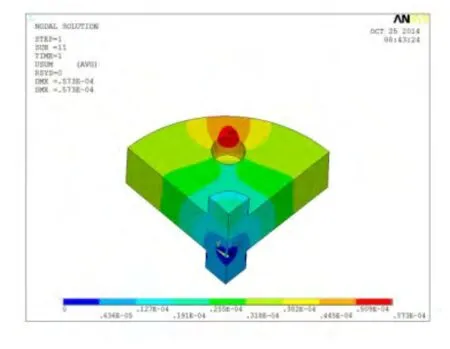
图4 小间隙配合关系下转子部件变形云图

其中转子部件与实验对象的相对变形量构成了该设备安装孔结构在工作状态下的动态误差，因此转子部件的最大变形量DMAX1及实验对象的最大变形量DMAX2即为随机基本变量响应值，同时为极限状态函数的目标变量。

基于人工神经网络的极限状态函数拟合分析

通过对转子部件及实验对象进行有限元计算分析后得到对其可靠性影响较大的参数如下，结构参数：安装孔孔径r1，实验对象半径r2，转子部件厚度h1，安装孔孔深h2，实验对象高度h3；材料参数：转子部件弹性模量E1，实验对象弹性模量E2；工作参数：转速v[5~7]。

经试验测得各个随机变量概率特性如表1所示。

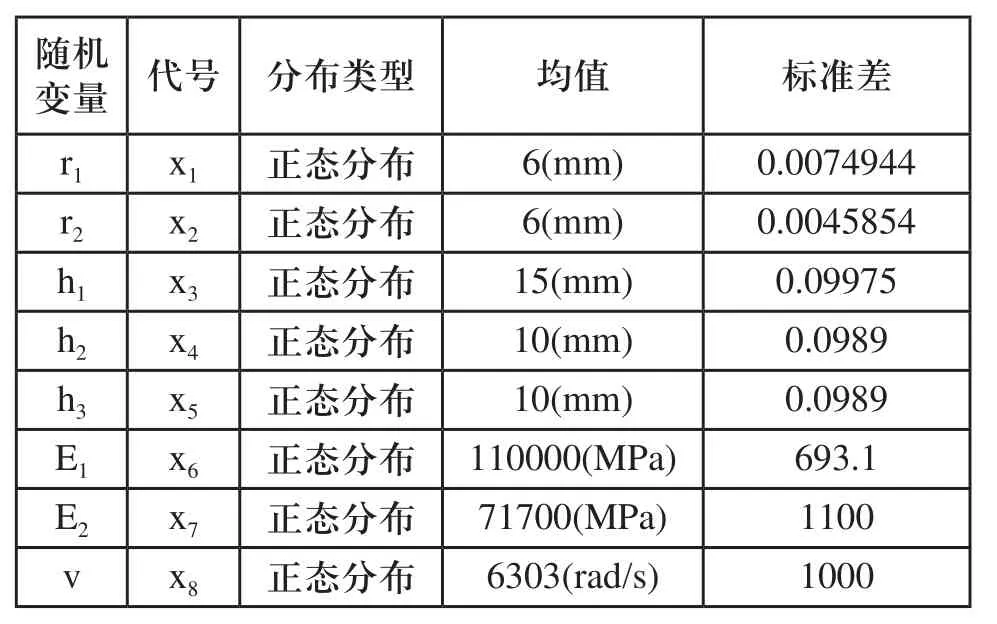
表1 随机变量概率分析表

采用试验设计方法中的超立方拉丁抽样方法进行DOE试验，试验次数为100次，集成ANSYS有限元软件得到随机变量和响应的样本值，响应的样本值如图5所示。其中DMAX1为实验对象最大变形量，DMAX2为转子部件安装孔位置最大变形量，水平坐标为运算次数，单位为1，垂直坐标为响应值的，单位为m。

根据样本点分别建立以DMAX1、DMAX2为输出参数的多元二次回归模型，随机变量基本多元二次回归模型为：

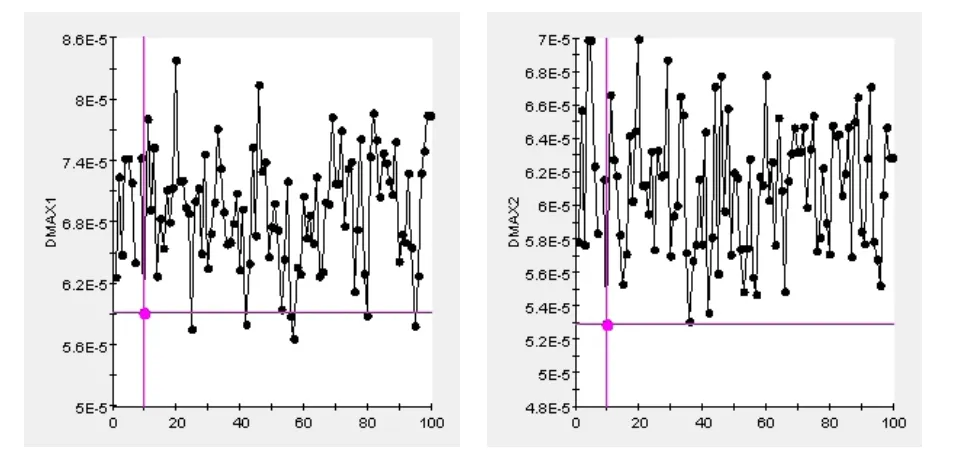
图5 有限元计算的最大变形量分布图

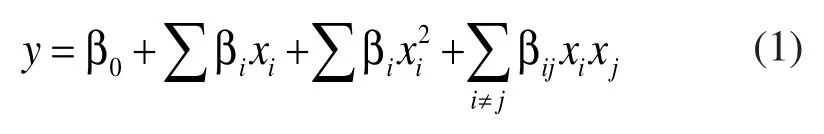
通过对样本响应值进行分析可知，对于转子部件的安装孔位置处的变形量(DMAX2)可造成影响的主要因素为转子部件弹性模量、转速、实验对象材料弹性模量；实验对象高度、安装孔深度、转子部件厚度、实验对象半径，安装孔半径。

根据零件尺寸公差与尺寸链可以构成一个闭环的原理，实验对象与转子部件变形差状态方程和可靠度R的表达式分别为：

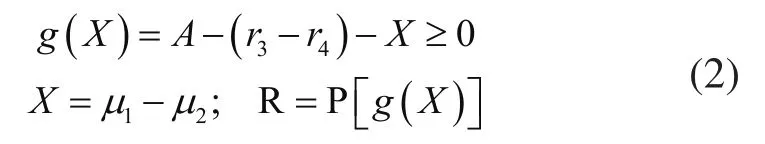
其中，通过µ1、µ2为转子部件安装孔附近最大变形量及实验对象最大变形量，r3为安装孔半径，r4为实验对象半径，A为转子部件与实验对象装配尺寸链。根据训练样本，分别建立以DMAX1，DMAX2为输出的基于遗传算法优化的神经网络模型。则实验对象的最大变形量（DMAX1）与随机变量之间函数关系以及转子部件的最大变形量（DMAX2）与随机变量之间函数关系：

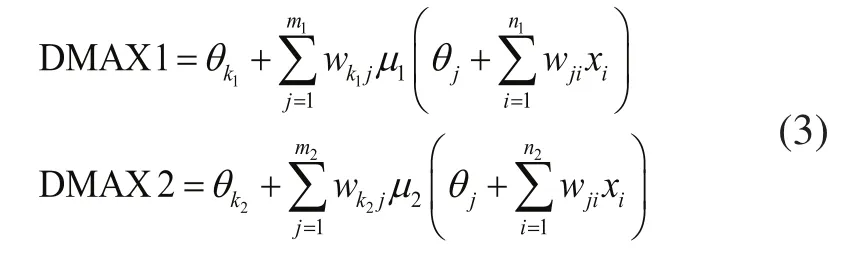
本文依据谢菲尔德大学遗传算法工具箱构造基于遗传算法优化的BP神经网络模型[8]。定义种群大小为40，个体长度为10，代沟为0.95，交叉概率为0.7，变异概率为0.01，经过50次迭代，得到进化曲线，图6为以DMAX1为输出变量的模型进化曲线。

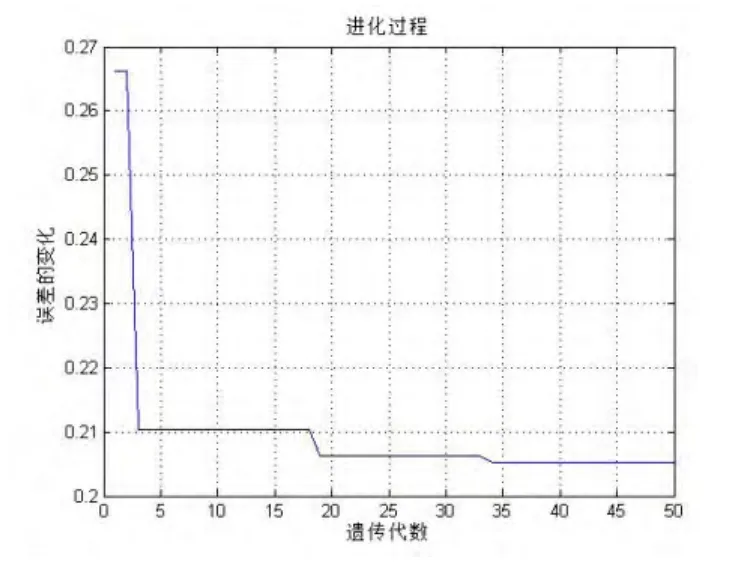
图6 进化过程曲线

在经遗传算法优化的初始权值和阈值的基础上，经过反复训练，使神经网络得到的样本十分接近DOE实验有限元样本响应，以DMAX1为输出变量的神经网络参数如表2所示。

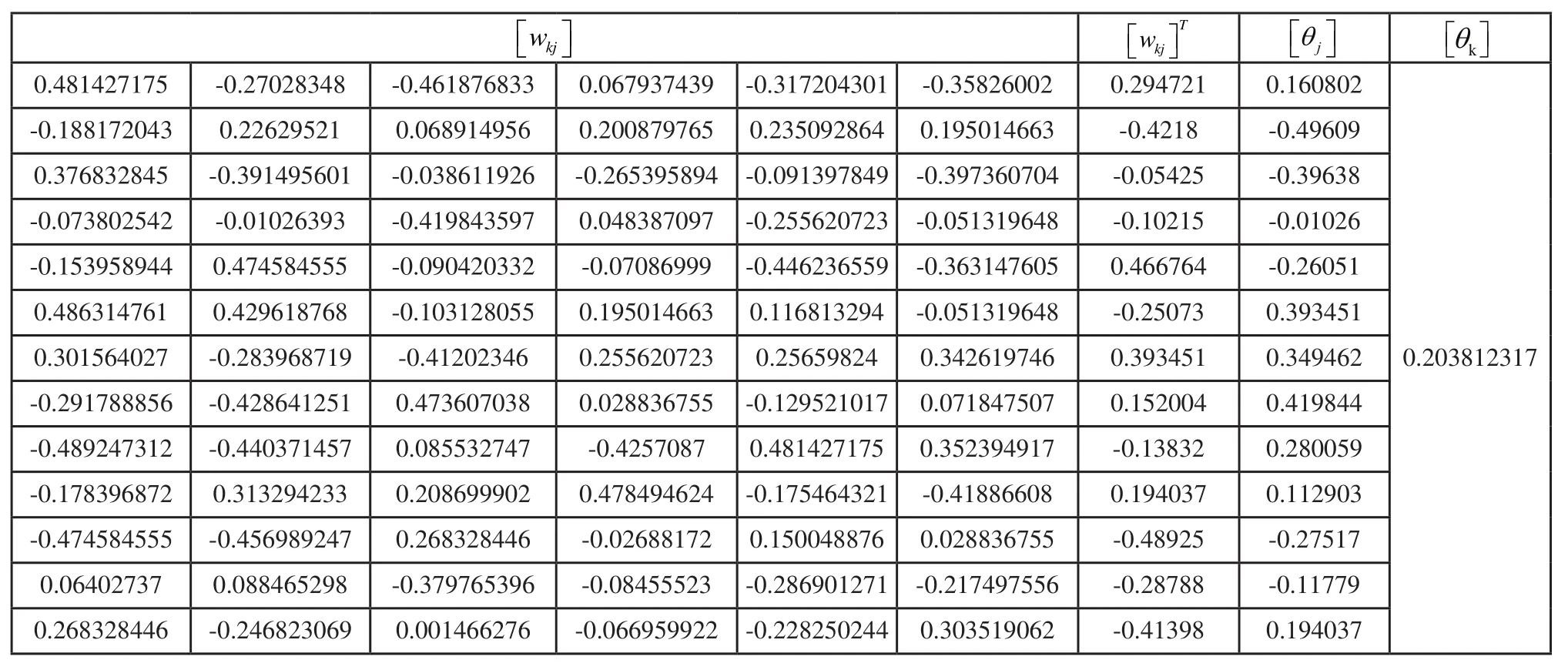
表2 训练后的神经网络参数

2 转子部件结构可靠性分析

误差在设计环节中根据公差限定初始范围，制造过程中形成的结构静态误差在工况参数影响下演变为动态误差，并对设备运行产生影响[9]。特别是对具有精密配合关系、受到强应力作用、产生较大应变的转子部件的动态特性影响更为显著，成为影响转子结构可靠性的重要因素。

当转子结构受到随机激励的作用下，定义动态误差可靠度：

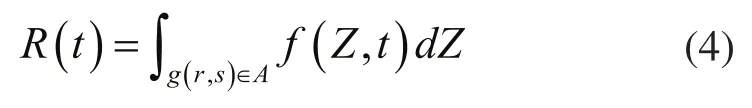
根据概率论相关知识，极限状态函数的前四阶矩为：

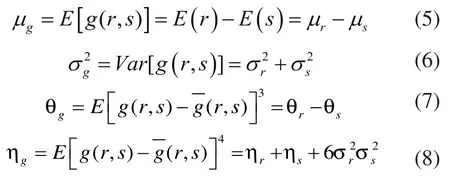
可靠性指标定义为：

其中，E(•)为期望值；µg、σg分别为状态函数的均值和方差。

由于基本随机变量均服从于正态分布，为简化问题，动态误差可靠度可以定义为在运动时域内，转子部件动态误差未超过许用误差范围的概率，即：

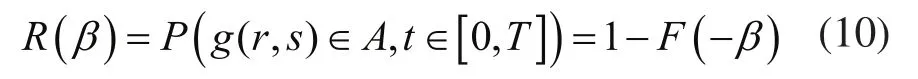
其中，F(-β)为关于-β概率分布函数的近似标准正态分布表达式。

为了得到动态误差响应的统计特征，根据可靠性的摄动技术，动态误差响应函数的前四阶矩µs、σs、θs、ηs表示为：

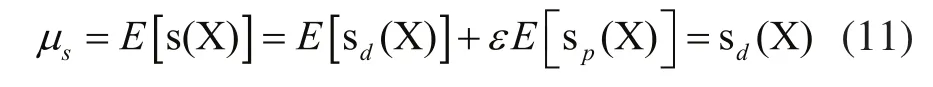
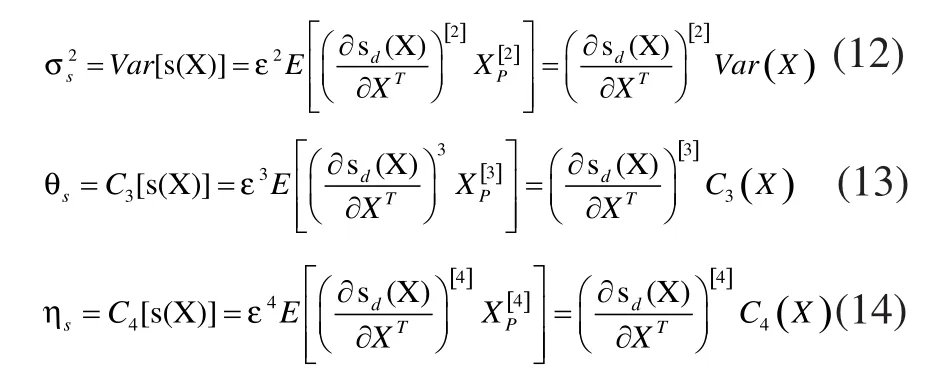
式中，C3(•)、C4(•)表示三阶中心矩和四阶中心矩。

在已知基本随机变量前四阶矩的前提下，将式（4）带入式（11）～式（14）得到随机响应的前四阶矩 µs、σs、θs、ηs，然后将式（11）～式（14）带入式（5）～式（8），可以得到状态函数的前四阶矩 µs、σs、θs、ηs。根据式（10）可得到系统的动态误差可靠度。

可靠度对基本随机变量参数XT的均值灵敏度为：

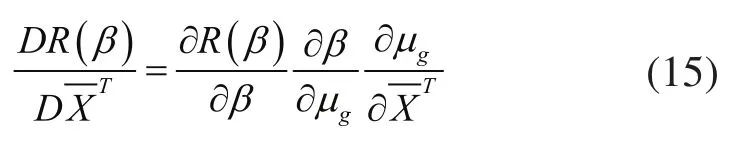
通过以上公式即可计算得出转子部件安装孔结构动态误差可靠度以及基本随机变量的可靠性灵敏度。

3 转子部件结构可靠度及可靠性灵敏度计算分析

由于转子部件为实验对象不具备替换性，因此在转子部件与实验对象构成装配关系时，配合代号选择基孔制的因为这种配合方式配合间隙较小，最小间隙为零的间隙定位配合较好的对准中心，一般多用于常拆卸场合，适合本案例工作要求。根据GB/T 1800.2-2009，孔直径为12mm，公称尺寸为H7的安装孔尺寸：直径为12mm，公称尺寸为h6的实验对象尺寸：。

装配尺寸链计算公式为：

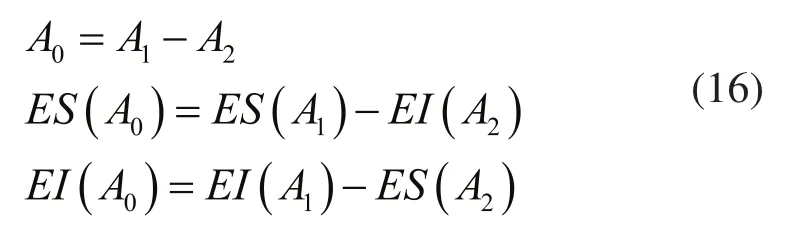
利用蒙特卡洛法验算，在选定的转子部件与实验对象的配合关系情况下，通过iSIGHT软件集成MATLAB和蒙特卡洛模拟模块，进行蒙特卡洛模拟实验，MATLAB输出变量Y为因此设定时，针对变形这一可靠性评价指标来讲转子部件安装孔是可靠的，其他随机变量均值及方差保持不变，设定抽样方式为描述抽样500次。对实验结果进行分析，输出变量均值为0.0073226(mm)，可靠度R1=0.884。本文方法与蒙特卡洛模拟法计算可靠度结果近似，误差为5.65%，因此该方法的计算精度在可接受范围内。通过计算结果可知，转子部件安装孔结构的动态误差可靠度虽远离可靠度临界值但是仍可通过更改设计方案将其进一步提高，因此对基本随机变量对转子部件结构可靠度影响情况分析，计算随机变量的均值可靠性灵敏度为：

结合可靠性和可靠性灵敏度相关理论，对转子结构可靠度对基本随即变量均值的灵敏度进行分析得实验对象半径r2，转子部件厚度h2，实验对象弹性模量E2，转速v的均值增大，其结果将使结构可靠度增大，结构趋于安全（失效概率变小）。安装孔孔径r1，安装孔孔深h2，实验对象高度h3，转子部件弹性模量E1的均值增大，其结构将使结构可靠度降低，结构趋于失效。

可靠度对基本随机变量均值的灵敏度排序为，安装孔孔径r1，转子部件厚度h1，实验对象半径r2，实验对象弹性模量E2；实验对象高度h3，安装孔孔深h2，转速v，转子部件弹性模量E1。这个排序表明了这些参数的改变对转子结构可靠度的影响程度。在产品设计、制造、使用过程中，应优先控制灵敏度排序靠前的随机变量，可以较好的提高结构的可靠度。

4 结束语

本文基于人工神经网络技术、随机摄动技术、可靠性设计和可靠性灵敏度相关理论，分析了具有随机参数的非线性转机结构动态误差，并对其可靠性进行了研究，给出了相应的计算方法，并对实际案例进行计算。通过与蒙特卡洛模拟法计算得出可靠度进行对比，该方法计算结果较准确，可以作为一般方法应用到此类问题的解决中。

应用本文方法能够有效的反应各个随机变量对其失效的影响程度，实现了对复杂非线性转子结构的可靠性灵敏度求解。在工程实际中，转子结构的结构参数和工况参数都十分复杂，本文方法具有通用、快速、有效的特点，使可靠性分析方法在工程实际中的应用更进一步。

[1]Shrawan Kumar，Yogesh Narayan，Tyler Amell.Role of awareness in head-neck acceleration in low velocity rearend impacts[J].Accident Analysis and Prevention,2000(32),233-241

[2]付汝辑.转子动力学的现代发展状况[J].机械强度,1980,04:10-26.

[3]韩清凯,于涛,俞建成,闻邦椿.单跨双圆盘不平衡转子一轴承系统的非线性动力学分析[J].机械工程学报,2004,40(4):16-20.

[4]王成林.一种适用于大转动惯量固体的高加速度承载实验装置动态特性分析[J].制造业自动化,2012,07:84-89.

[5]张根保,王国强,何文辉,曾海峰.基于任务的数控机床可靠性分配技术研究[J].中国机械工程,2010,19:2269-2273.

[6]何明礼,向晓东,郭尹亮.基于重要度的系统可靠性分配方法[J].安全与环境工程,2009,04:62-65.

[7]梁震涛,陈建军,胡太彬.星载天线展开机构系统可靠性分配的未确知方法[J].南京理工大学学报(自然科学版),2007,05:579-584.

[8]王赟松,许洪国.快速收敛的BP神经网络算法[J].吉林大学学报(工学版),2003,04:79-84.

[9]金明杰,楼云江,刘冠峰,凌强.基于自适应动态碰撞检测的工业机器人运动规划算法研究[A].中国自动化学会控制理论专业委员会、中国系统工程学会.第三十一届中国控制会议论文集C卷[C].中国自动化学会控制理论专业委员会、中国系统工程学会,2012:6.