2015年浙江理科第6题赏析

●张晓东 (桐乡市高级中学 浙江桐乡 314500)

2015年浙江理科第6题赏析

●张晓东 (桐乡市高级中学 浙江桐乡 314500)

2015年浙江省数学高考理科试卷的亮点很多，其中第6题更是清新靓丽、超凡脱俗，不仅题型新颖，而且寓意深刻.

例1设 A，B是有限集，定义:d(A，B)= card(A∪B)－card(A∩B)，其中card(A)表示有限集A中的元素个数.

命题①:对任意有限集A，B，“A≠B”是“d(A，B)＞0”的充分必要条件;

命题②:对任意有限集 A，B，C，d(A，C)≤d(A，B)+d(B，C).

A.命题①和命题②都成立

B.命题①和命题②都不成立

C.命题①成立，命题②不成立

D.命题①不成立，命题②成立

1 解法分析

解法1(韦恩图)

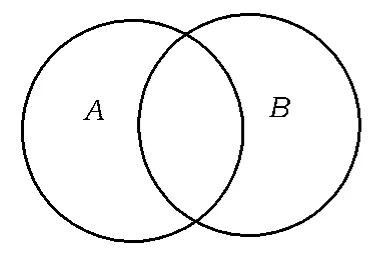
图1

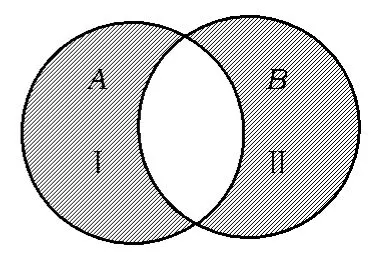
图2

对于命题①，不妨把图画成图1，若A∩B=φ，只要把A，B公共部分看成没有元素，当A⊆B或者B⊆A时，也只需将相应区域看成没有元素.

于是，d(A，B)为图2中的阴影部分，若A≠B，则可得区域Ⅰ与区域Ⅱ中不可能都没有元素，因此d(A，B)＞0;又若d(A，B)＞0，则区域Ⅰ与区域Ⅱ中不可能都没有元素，因此A≠B，故命题①成立.

图3

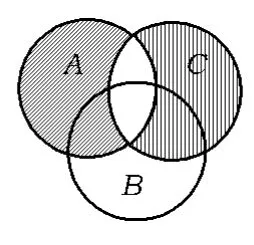
图4

图5

对于命题②，不妨把图画成图3，若2个集合的交集为φ，只要把相应2个集合公共部分看成没有元素.若一个集合是另一个集合的子集，也只需要将相应部分看成没有元素.

于是，d(A，C)为图 4中的阴影部分，d(A，B)+d(B，C)为图5中的阴影部分，显然图4的阴影部分包含在图5的阴影部分中，因此命题②成立.故选A.

解法2(容斥定理)

显然，card(A∪B)≥card(A∩B)，当且仅当A∪B=A∩B时等号成立，而A∪B=A∩B⇔A=B，故命题①成立.

对于命题②，由容斥定理 card(A∪B)=

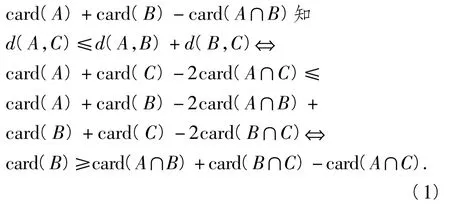
因为card(A∩C)≥card((A∩B)∩(B∩C))，所以要证明式(1)，即证

亦即证card(B)≥card((A∩B)∪(B∩C))，此式显然成立.故命题②成立.

2 背景分析

在泛函分析中有一个基本定义［1］:

给定非空集X，实数集R.如果存在一个X×X到R的二元函数ρ(x，y)满足条件:

1)ρ(x，y)≥0，而ρ(x，y)=0的充要条件是x=y(非负性);

2)ρ(x，y)=ρ(y，x)(对称性);

3)ρ(x，z)≤ρ(x，y)+ρ(y，z)(三点不等式)，则称X是以ρ为距离的距离空间，简记为(X，ρ).ρ称为X上的一个距离函数，以上3个条件称为距离公理.

如n维欧几里得空间Rn内任意2个点x= (x1，x2，…，xn)，y=(y1，y2，…，yn)的距离定义为，则欧几里得空间Rn是以d为距离的距离空间.

显然d(x，y)满足距离公理中的条件.回到原题，设X是由所有有限集合组成的集合，d(A，B)= card(A∪B)－card(A∩B)给出了一个从X×X到R的二元函数.

显然d(A，B)满足对称性(条件2)，由解法分析知道d(A，B)满足非负性(条件1)与三点不等式(条件3)，因此X可看成以d为距离的距离空间.

3 变式分析

该题以“距离空间”为背景考查了学生集合的知识、简易逻辑的知识，同时考查了学生的数学理解能力以及分析问题、解决问题的能力，笔者尝试从以下3个方向作了模仿与变式.

方向1集合运算

例2设 A，B是有限集，定义:，其中card(A)表示有限集A中的元素个数，则下列不一定正确的是

( )

分析因为card(A∪B)≥card(A∩B)，所以选项A，B都正确.又

因此选项C不一定正确，选项D正确.故选C.

方向2函数概念

例3已知函数f(x)的定义域为A，值域为B，定义f(Ai)={f(x)|x∈Ai，Ai⊆A}，f－1(Bi)={x| f(x)∈Bi，Bi⊆B}，其中i=1，2.则下列运算中不正确的是 ( )

A.f(A1∪A2)=f(A1)∪f(A2)

B.f(A1∩A2)=f(A1)∩f(A2)

C.f－1(B1∪B2)=f－1(B1)∪f－1(B2)

D.f－1(B1∩B2)=f－1(B1)∩f－1(B2)

分析如图6，对任意 x∈A1∪A2，f(x)∈f(A1)∪f(A2)，有

又对任意f(x)∈f(A1)∪f(A2)，x∈A1∪A2，从而f(x)∈f(A1∪A2)，于是

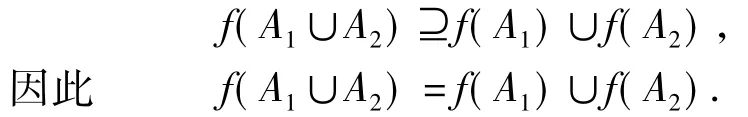
故选项A正确.

如图6，存在x1∈A1，x2∈A2，x1≠x2，f(x1)= f(x2)=a，使得 a∈f(A1)∩f(A2)，但a∉f(A1∩A2)，故选项B不正确.

如图 7，对任意 y∈B1∪B2，f－1(y)∈f－1(B1)∪f－1(B2)，从而

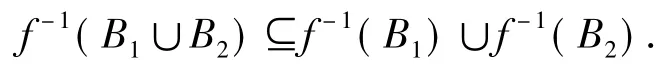
又对任意f－1(y)∈f－1(B1)∪f－1(B2)，y∈B1∪B2，从而

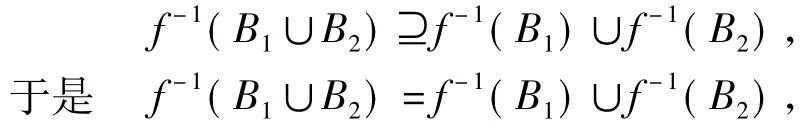
故选项C正确.

图6

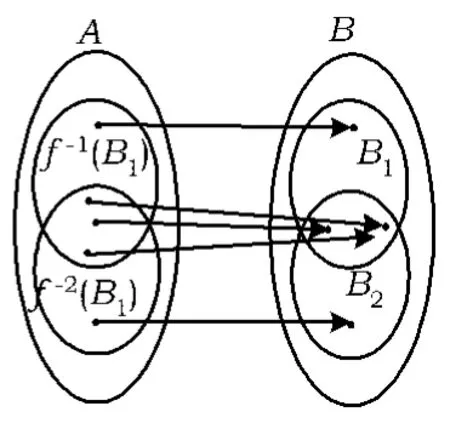
图7

如图 7，对任意 y∈B1∩B2，f－1(y)∈f－1(B1)∩f－1(B2)，从而

又对任意f－1(y)∈f－1(B1)∩f－1(B2)，y∈B1∩B2，从而

故选项D正确.

因此，答案是B.

方向3距离空间

例4设平面向量 an=(xn，yn)，xn，yn∈R， n∈ N*.定 义:，其中i，j∈N*.

命题①:对任意ai，aj，ai≠aj是d(ai，aj)＞0的充分必要条件;

命题②:对任意i，j，k∈N*，d(ai，ak)≤d(ai，aj)+d(aj，ak).

A.命题①和命题②都成立

B.命题①和命题②都不成立

C.命题①成立，命题②不成立

D.命题①不成立，命题②成立

分析显然命题①成立.

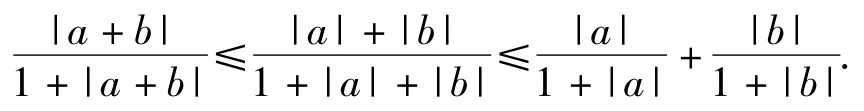
令a=xi－xj，b=xj－xk，则

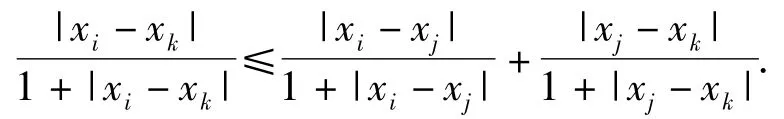
同理可令a=yi－yj，b=yj－yk，则

2个式子相加，得

从而命题②成立.故选A.

4 功能分析

对于数学水平较弱的学生，他们在解该题时主要是通过特殊探路法，通过举一些特例来帮助作出判断.

如令A={1，2，3}，B={2，3，4}，C={4，5}，则d(A，B)=4－2=2＞0，于是估计命题①是正确的.又d(B，C)=4－1=3，d(A，C)=5－0=5，d(A，C)≤d(A，B)+d(B，C)，于是估计命题②也是正确的，于是猜想答案是A.他们在解决该题时用了特殊探路的方法，虽然提高了猜答案的正确率，但是这种方法仍然是风险很大的.

对于数学水平中等的学生，他们解决该题的方法不局限于特殊探路法，他们更多的会利用韦恩图来帮助探索问题.但是由于2个集合的关系不定，而他们又不会把任意2个集合的韦恩图看成图1来理解，于是进行了分类讨论.对于命题①，他们分成A∩B=φ，A⊆B，B⊆A这3类来讨论.而对于命题②，如果仍然要分类，显然，时间不允许，于是他们更多的是挑了几种进行研究，结果发现都满足命题②，于是判断命题②也是正确的.

尽管这种方法还不足以判断命题②是正确的，但是他们比第1类学生作了更多的尝试与探索，他们用到了分类讨论、以形助数的思想，判断比前者更可靠一些.

对于数学水平较高的学生，他们能整体把握问题，能够运用抽象的数学符号来进行运算与思考，即使是用韦恩图，他们也能够把3个集合的关系不失一般性地看成图3.由于他们的思维水平比前2类学生高，他们的方法是可靠的，因此能够作出正确的判断，而且花的时间也不多.对这类学生而言，解决该题的同时收获了解题的成就感，使他们以更好的状态去解决下面的问题.

一道好的试题应该让不同程度的学生均有所收获，选择题也是如此.

(感谢笔者的导师——浙江师范大学张维忠教授对本文写作的指导与帮助，感谢“浙江省桐乡市名师奠基工程”项目对本研究的大力支持.)

［1］孙永生，王昆扬.泛函分析讲义［M］.北京:北京师范大学出版集团，2007.