“通法”与“特技”齐飞——2015年浙江理科第14题的解法探究

●盛耀建 (湖州中学 浙江湖州 313000)

“通法”与“特技”齐飞
——2015年浙江理科第14题的解法探究

●盛耀建 (湖州中学 浙江湖州 313000)

2015年的高考已经圆满落下帷幕，后续工作也在有条不紊地进行中，但对考题的品味还远未结束，其中浙江理科第14题给笔者印象最为深刻.细细研究得到多种解法，且称之“通法”与“特技”齐飞，望对今后的教学起到一定的指导作用.

1 考题再现

题目若实数x，y满足x2+y2≤1，则|2x+ y－2|+|6－x－3y|的最小值是______.

(2015年浙江省数学高考理科试题第14题)

分析1)由实数x，y满足x2+y2≤1可知，点(x，y)在圆饼区域x2+y2≤1上运动;2)求|2x+ y－2|+|6－x－3y|的最小值，该式中含有2个绝对值，意味着该题有一定的难度，同时也提供了解题的3个思路:要么去掉绝对值，要么不等式放缩，要么找出其几何意义.

2 解法探究

2.1 去绝对值

当问题中出现绝对值时，题目往往不会简单，而我们常用的一种思路就是去绝对值，去绝对值的方法很多，比如平方、分类讨论、可行域等等.

解法1(线性规划)实数x，y满足x2+y2≤1，由图1知6－x－3y＞0.

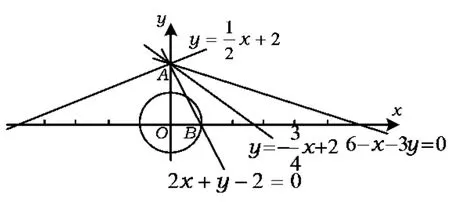
图1

点评上述解法涉及线性规划及直线和圆位置关系等知识，结合分类讨论的思想方法巧妙地去掉了绝对值，并从图像上进行分析快速得到了最优解，从而求出了最小值，在方法上具有一定的推广可能，属于“通法”.

链接若实数x，y满足x2+y2≤5，则3|x+ y|+|4y+9|+|7y－3x－18|的最大值是 ( )

(2015年浙江省暨阳联谊学校高三联考数学理科试题第8题)

分析因为实数x，y满足 x2+y2≤5，所以4y+9＞0，且7y－3x－18＜0.

点评由条件实数x，y满足x2+y2≤1，想到三角换元的思想，同解法1结合图像进行分类讨论，从三角函数知识角度求得最小值.

2.2 不等式放缩

题中求|2x+y－2|+|6－x－3y|的最小值，可联系绝对值三角不等式进行放缩，等号成立时即可求出最小值.

解法3|2x+y－2|+|6－x－3y|≥|x－2y+4|=|x－2y+1+3|，易知当且仅当2x+y－2与6－x－3y一正一为0或同为正时等号成立.由图2知此时x－2y+1≥0，从而|x－2y+1+3|≥3，即原式的最小值为3，当且仅当时等号成立.

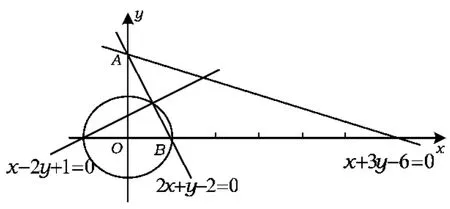
图2

点评解法3采用了绝对值三角不等式进行放缩，借助可行域寻找等号成立的条件，从而找出最小值，针对此题十分有效.

解法4|2x+y－2|+|6－x－3y|≥|3x+4y－8|，当且仅当2x+y－2与6－x－3y一正一为0或异号时等号成立.由柯西不等式得

点评该解法采用了绝对值三角不等式的另外一个形式，利用柯西不等式进行二次放缩，借助柯西不等式等号成立的条件及x2+y2=1找出等号成立时x与y的值，从而找出最小值，方法简易，堪称一绝.

2.3 找几何意义

笔者看到问题中的|2x+y－2|+|6－x－3y|时，联想到了点到直线的距离公式:

图3

点评解法5技巧性很强，先将原式化成点到直线的距离形式，利用图像及借助直线l1与l2夹角大小的特殊性，从几何意义出发巧妙求出最小值.解法5虽可适当推广(如下面的变式)，但还是有一定的局限性，对系数要求较高，绝对值的个数仅限于1个或2个，属于“特技”.

变式若实数x，y满足x2+y2≤1，则的最小值是______.

分析同解法5，

从上易知，可根据解法5中2条直线的夹角大小设计一定的系数即可改编出新的试题.

3 探究体会

1)高考作为选拔性的考试，在试题设计上表现为重点考查“通性通法”，并适当加入“技巧元素”.因此在平时的教学过程中，教师应注重“通法”的教学，强化学生的计算能力，适当补充对解法技巧的渗透.

2)本题的解法虽然多种多样，但它们并不一定适合每一位学生，这就要求教师在教学过程中针对不同的授课对象选用不同的解法进行讲解，如:在普通班教学时应重点介绍解法1，并根据需要适当进行解法3与解法5的讲解;而对实验班学生则在讲解解法1、解法3与解法5的基础上还可适当注入解法2与解法4的解题思想.