数形结合彰双翼 探源溯流显本质——以2015年浙江理科第15题为例

●蔡剑锋 (余杭第二高级中学 浙江杭州 311100) ●陈朝阳 (余杭区教育局教研室 浙江杭州 311100)

数形结合彰双翼 探源溯流显本质
——以2015年浙江理科第15题为例

●蔡剑锋 (余杭第二高级中学 浙江杭州 311100) ●陈朝阳 (余杭区教育局教研室 浙江杭州 311100)

2015年高考落下帷幕，研究浙江省的数学高考试题，不乏许多立意高、角度宽、视点多且注重开发考查学生数学思想方法的题目，同时考查了学生的理性思维能力，对数学本质的理解能力，以及数学知识之间的相互联系及应用能力.其中理科第15题——向量填空题在这几个方面表现得更是淋漓尽致.

向量以其兼具“代数”与“几何”的双重形态，成为实施数形结合的有效工具，备受高考命题者的亲睐，浙江省数学高考的向量题往往是试卷的一大亮点，在考查上逐步加深与灵活，演绎得更加唯美.2015年这道向量考题与前几年高考试题风格背景有相似之处，同时解题思路也有关联性，是前几年试题的沿袭与承接，更有创新.下面笔者就该题的解题过程谈谈自己的体会和感受.

1 原题回顾析立意

例1已知e1，e2是空间单位向量，，若空间向量满足b·e1=2，，且对于任意x，y∈R，|b－(xe1+ye2)|≥|b－(x0e1+ y0e2)|=1(其中x0，y0∈R)，则 x0= ______，y0= ______，|b|=______.

(2015年浙江省数学高考理科试题第15题)

该题通过空间向量的平台，利用不等关系，体现最小值的本质.问题的结构特点给考生多角度的思考空间，同时丰富了填空题的形式，出现一题三空且相互制约.

2 解法分析求灵活

2.1 基底法

令m=xe1+ye2，则

解法1(转化为二次方程在R上恒成立)

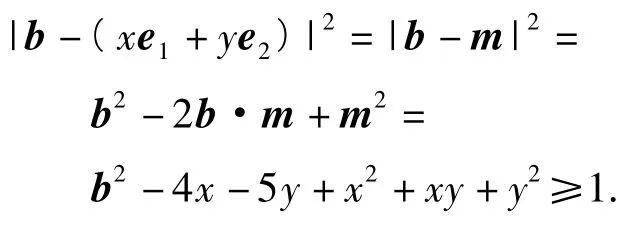
即关于x的不等式

恒成立，从而

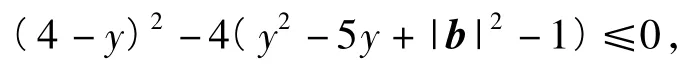
即对任意实数y都有

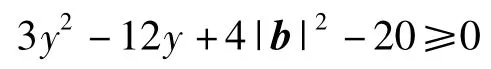
成立，因此

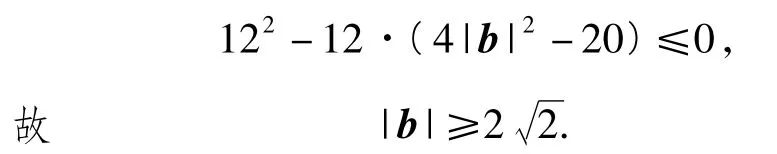
又对于任意x，y∈R，|b－(xe1+ye2)|≥|b－(x0e1+y0e2)|=1(其中x0，y0∈R)，于是

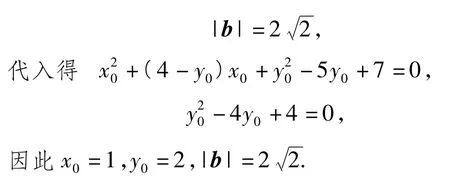
解法2(配方)

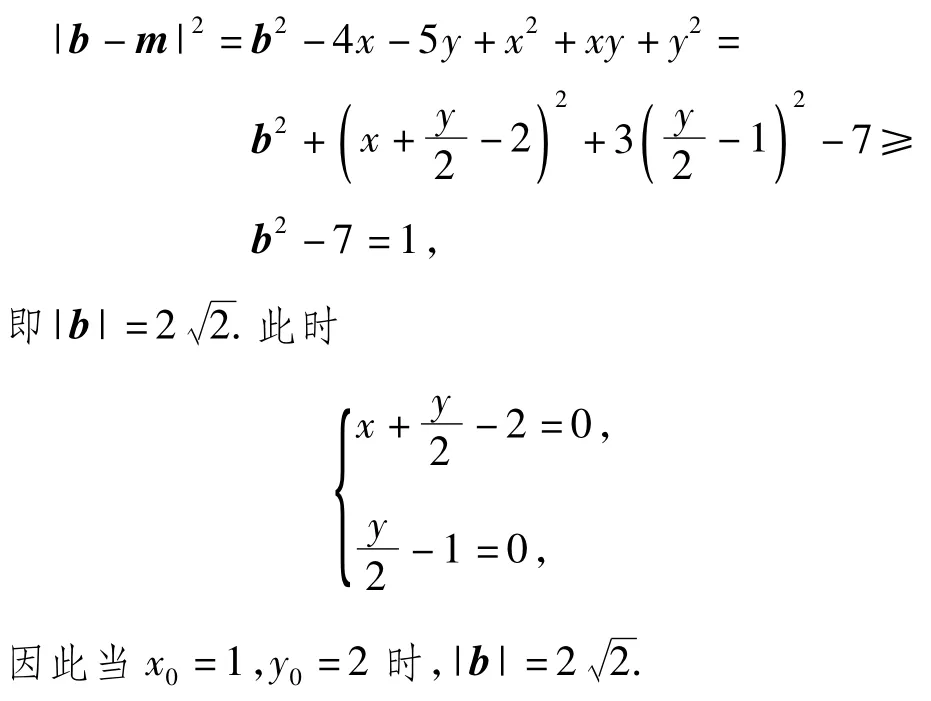
解法3(不等式处理，换元成二次函数)

评析模运算的基本处理方法是对向量进行平方，构造相应的目标函数，再来求解函数的最值.此解法的难点是在空间向量的背景下平方得到了一个求二元变量的最值问题.上述3种解法对学生的思维要求较高，学生不容易把握.

2.2 坐标法

解法4如图1建立空间直角坐标系，其中e1=(1，0，0)，.设b=(m，n，t)，则

图1

又|b－(xe1+ye2)|≥|b－(x0e1+y0e2)|=1(其中x0，y0∈R)，即

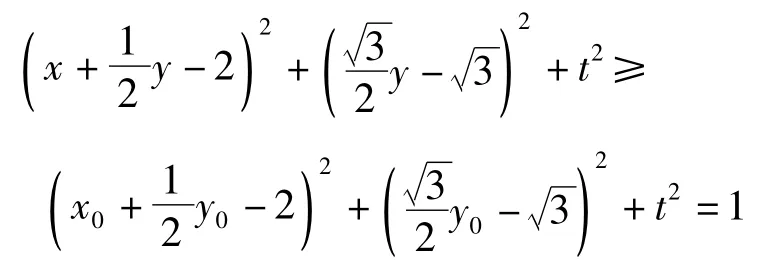
对任意的x0，y0∈R恒成立，从而当

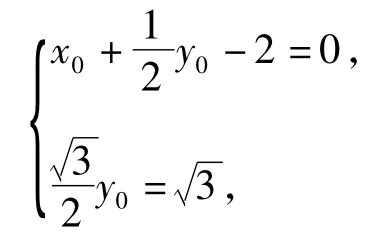
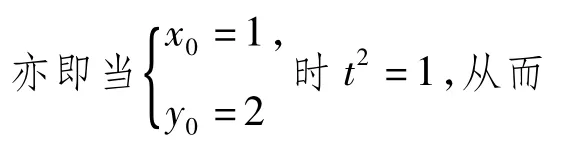
评析坐标法的本质与解法1的配方处理是一致的，其直观之处在于通过坐标形式的模运算直接得到

与解法1相比更加直观，学生容易理解.同时我们发现这时b－(e1+2e2)=(0，0，t)与z轴平行，即与e1，e2确定的平面垂直，隐含了几何特点，预示着本题可以用几何法解决，是数形结合的一种统一.

2.3 几何法

分析数形结合，整体把握，这要求学生理解|b－(xe1+ye2)|表示的是点B到向量e1·e2确定的平面上任意一点的距离，再理解最小值的含义就非常清楚了.考生在这里若能嗅到几何的芬芳，看透空间向量问题，则“b·e1=2，”就直接转化为同一平面内的.

3 真题研究探源头

浙江省自主命题以来此类型的题目不断出现，其实它在不断完善，把试题演绎得更加完美.考生若不能识别它的真实面目，在考试时就很难越过向量题这道坎.

此类题最早出现在2005年浙江省数学高考理科第10题(选择压轴题).

例2已知向量a≠e，|e|=1，对任意t∈R，恒有|a－te|≥|a－e|，则 ( )

A.a⊥e B.a⊥(a－e)

C.e⊥(a－e) D.(a+e)⊥(a－e)

分析此题中向量是共面的，变量也只有一个t，因此模长平方得到的函数也是相对好处理的，这里主要是看|a－te|≥|a－e|的几何意义.

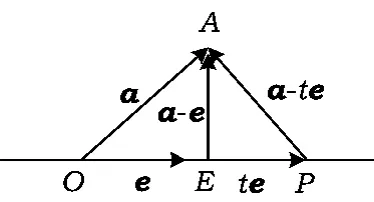
图3

4 立足教材揭本质

人教A版数学必修2第106页思考:已知点P0(x0，y0)，直线l:Ax+By+C=0，如何求点P0到直线l的距离?

此思考题先让学生明确“点到直线的距离”的概念:从几何角度看是指从点P0到直线l的垂线段的长度;从代数的角度看点P0与直线l上任一点的2点间距离的最小值(具体解法略).

人教社A版数学选修2-1第87页:如图4，l为经过已知点A且平行于已知非零向量a的直线，对空间任意一点O，点P在直线l上的充要条件是存在实数t，使，其中a叫做直线l的方向向量.在l上取，则.这2个式子都称为空间直线的向量表示式，即点P在直线AB上，当取最小值时，，即求得点P到直线AB的距离.

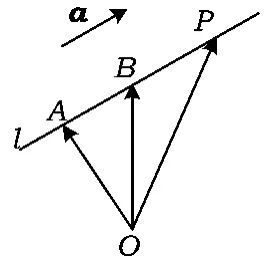
图4

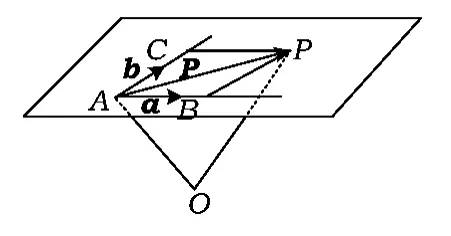
图5

这正是上述3个高考真题解法的由来.

人教社A版数学选修2-1第87页:如果2个向量a，b不共线，那么向量p与向量a，b共面的充要条件是存在唯一的有序实数对(x，y)，使 p= xa+yb.

如图5，空间一点P位于平面ABC内的充要条件是存在有序实数对(x，y)，使;或对空间任意一点O，.这2个式子都称为空间平面ABC的向量表示式.

在教学的过程中，我们往往注重共面情况的分析和讲解，注意到表示的正是空间一点O与平面ABC内任意一点P确定的向量，的最小值即为空间一点O到平面ABC的距离.

这正是几何解法的由来.

4 意识引领助教学

通过对这些向量高考题的分析知道:教师在平时的向量复习教学中应更加注重以下3个方面:

1)强化基底意识.基底法是解决向量问题的一个基本方法，是平面向量和空间向量基本定义的体现，在向量模长问题的处理上，a2=|a|2是一个重要的等式，它能实现向量的运算向代数运算的转化，是向量问题代数化的一个重要体现.

2)强化坐标意识.由于向量兼具着代数和几何的双重特征，很多问题我们可以通过建立平面直角坐标系，构建代数与几何之间的联系，通过坐标形式的代数语言翻译题目的条件，借助代数运算解决问题，着重体现函数和方程的思想.

3)强化几何意识.在向量运算过程中，树立几何特点的分析，直接构造图形，以形助数，使解题更加直观.

向量是沟通代数和几何的中间桥梁，将向量引入中学教学的一个重要原因是它既具有代数的形式又具有几何的特点，是刻画几何模型的一个重要工具.通过几何法可以轻松地解决相应问题，减少繁琐的运算，同时也引导一线教师在向量教学中要充分重视向量的几何特点，在平时的教学中逐步渗透给学生.