2015年高考安徽卷第18题证法探究及拓展

●梁昌金 (寿县第一中学 安徽寿县 232200)

2015年高考安徽卷第18题证法探究及拓展

●梁昌金 (寿县第一中学 安徽寿县 232200)

纵观近几年安徽省数学高考理科数列题，基本都是以“函数、数列不等式”为载体来考查学生对放缩法、数学归纳法等方法的掌握.然而这类试题的难度往往很大，学生不易掌握，甚至无从下手.现通过对2015年安徽省数学高考理科第18题第2)小题的证法探究，谈谈这类数列型不等式证明的常用方法.

1 真题展示

例1设n∈N*，xn是曲线y=x2n+2+1在点(1，2)处的切线与x轴交点的横坐标.

1)求数列{xn}的通项公式;

(2015年安徽省数学高考理科试题第18题)

2 背景探源

试题第2)小题研究的是乘积式数列不等式的证明问题，可看作是下列高考题的延续和创新.

例2等比数列{an}的前n项和为Sn，已知对任意的n∈N*，点(n，Sn)均在函数y=bx+r(其中b＞0且b≠1，b，r均为常数)的图像上.

1)求r的值;

2)当b=2时，记bn=2(log2an+1)，n∈N*，证明:对任意的n∈N*，不等式成立.

(2009年山东省数学高考理科试题第20题)

例3已知曲线Cn:x2－2nx+y2=0(其中n=1，2，…)，从点P(－1，0)向曲线Cn引斜率为kn(其中kn＞0)的切线ln，切点为Pn(xn，yn).

1)求数列{xn}与{yn}的通项公式;

2)证明:x1·x3·x5·…·x2n－1＜.

(2009年广东省数学高考理科试题第21题)

3 证法探究

思路1数学归纳法

所证不等式与自然数n有关，在无其他思路的情况下，首选当然是数学归纳法.

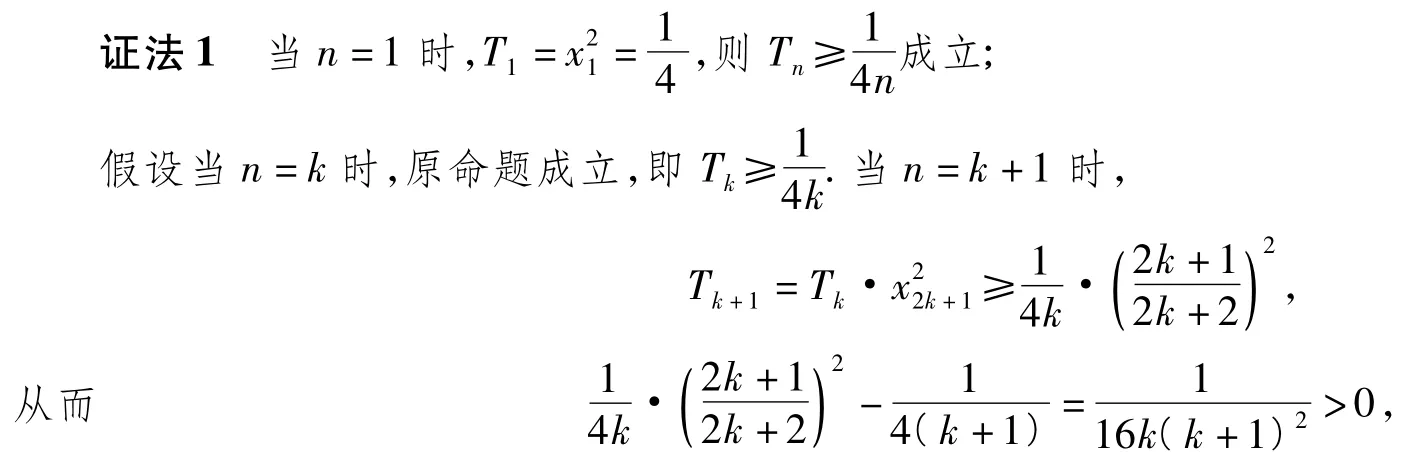
评注数学归纳法是一种重要的数学方法，其中第2步假设和递推是关键，特别是当n=k+1的证明较困难时，可依据待证目标作差或作商证明之.

思路2放缩法

放缩法本质上是利用不等式的传递性，把要证明的不等式加强为一个易证的不等式.放缩是一种重要的变形手段，难点在于目标不明确，尺度不好把握，技巧性太强.这样就显得放缩法很神秘，实质上，这类问题可以通过假设目标、建立递推关系，从而将放缩目标直接求出的方式处理.

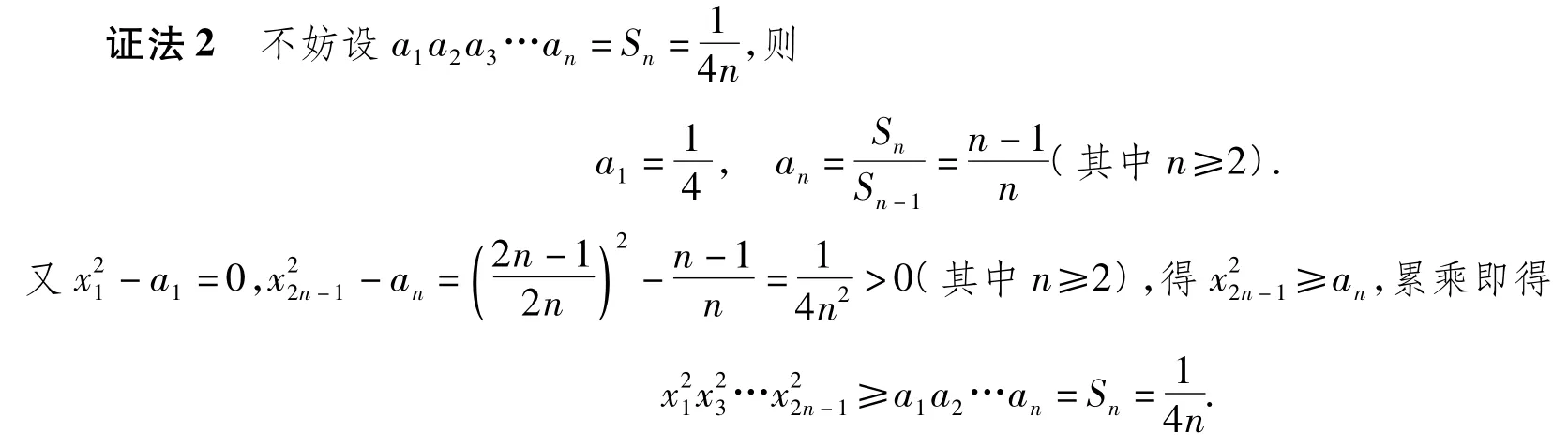
评注这种假设目标、建立递推关系，求出放缩目标的方法，消除了放缩法的神秘感，增强了考生解决问题的预见性.

思路3对偶法

所谓对偶法就是构造一个与原式相似的式子，以实现消元的目标，从而使不等式得以证明.

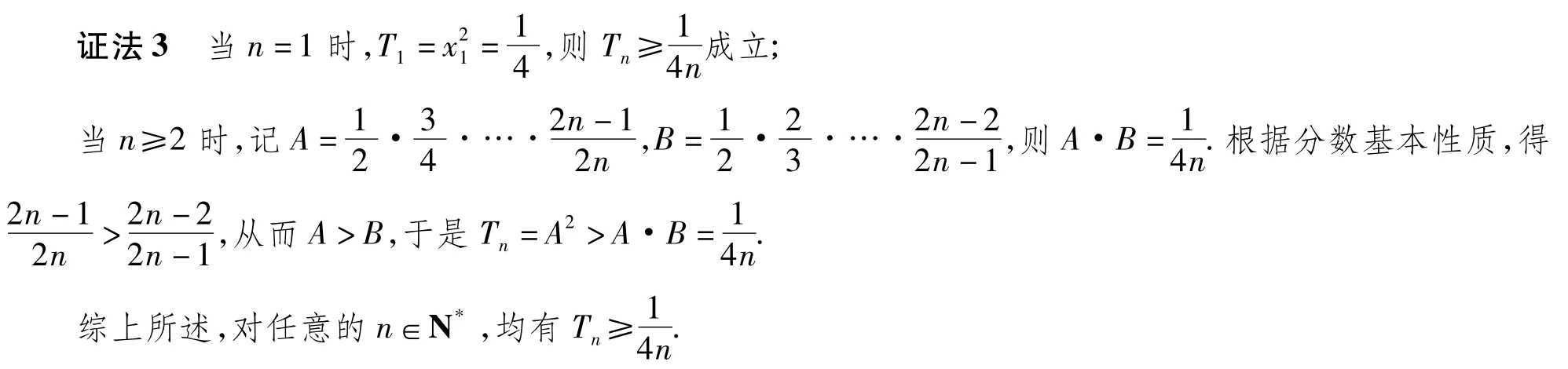
评注对偶法的关键是构造式子，达到消元的目的.

思路4构造函数，利用单调性求最值

由于数列是一种特殊的函数，因此数列不等式的证明问题，可以用函数的观点去观察、分析和讨论.

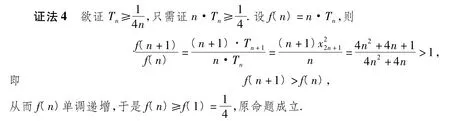
思路5利用基本不等式

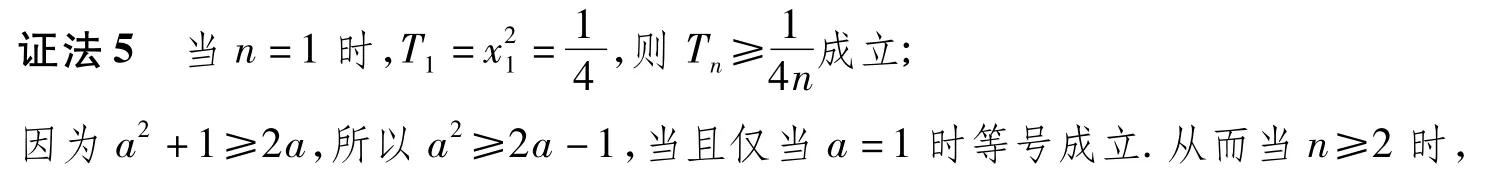
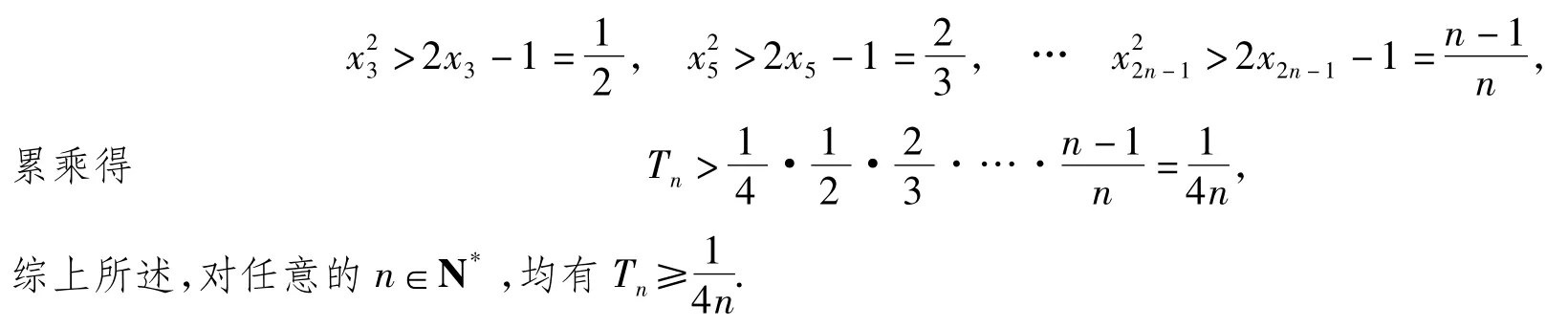
4 结论拓展

拓展2数列{an}是等差数列，首项a1＞1，公差d＞1，且a1，d，k∈N*，则

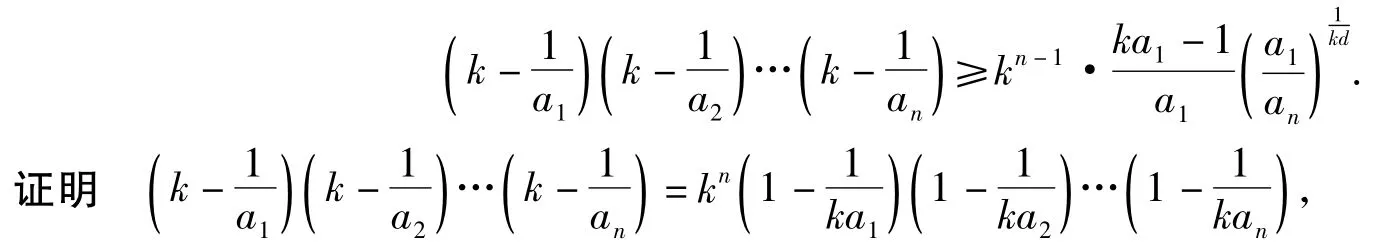
易知数列{kan}是公差为kd的等差数列，由拓展1可得

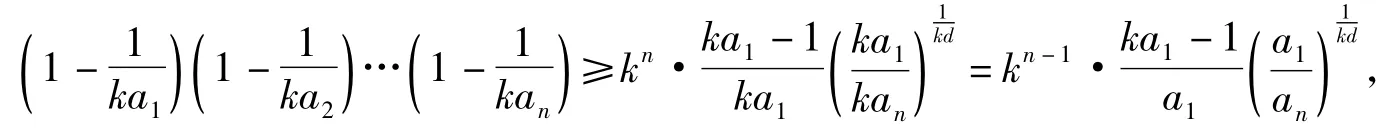
故结论成立.

拓展3数列{an}是等差数列，首项a1＞1，公差d＞1，且a1，d，k，m∈N*，m|kd，则

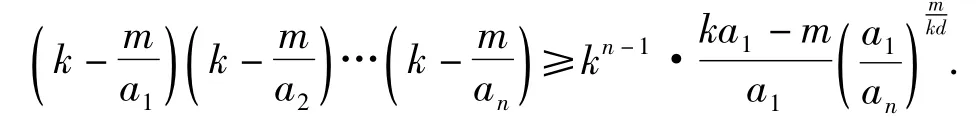
仿拓展1和拓展2可证，此处从略.

以上的拓展均要求数列{an}是等差数列，若{an}是等比数列，结论又如何呢?下面先举一个特例.

拓展5数列{an}是等比数列，且an∈(0，1)，则

利用数学归纳法易证，此处略.