透析考题信息 提升解题驱动力——赏析2015年湖北卷第21题

●岳 峻 (太和中学 安徽太和 236600)

透析考题信息 提升解题驱动力
——赏析2015年湖北卷第21题

●岳 峻 (太和中学 安徽太和 236600)

2015年数学高考湖北卷试题背景新颖，创新于数学史料加工，顺应于高考改革走向，融数学本质、数学素养和数学文化于一体，内涵丰富，思想深刻，给人耳目一新的感觉.笔者结合2015年湖北卷第21题，探讨如何透析考题信息，提升解题驱动力.

1 考题再现

题目一种作图工具如图1所示，O是滑槽AB的中点，短杆ON可绕O转动，长杆MN通过N处铰链与ON连接，MN上的栓子D可沿滑槽AB滑动，且DN=ON=1，MN=3.

当栓子D在滑槽AB内作往复运动时，带动N绕O转动一周(D不动时，N也不动)，M处的笔尖画出的曲线记为C.以O为原点，AB所在的直线为x轴建立如图2所示的平面直角坐标系.

图1

图2

1)求曲线C的方程.

2)设动直线l与2条定直线l1:x－2y=0和l2:x+2y=0分别交于点P，Q.若直线l总与曲线C有且只有1个公共点，试探究:△OPQ的面积是否存在最小值?若存在，求出该最小值;若不存在，说明理由.

2 考题条件的思维分析

首先，我们要根据作图工具实物的形象，抽象地建立一个数学模型.审题发现，本题的条件有:①DN=ON;②ON=1;③MN=3.隐含信息为:O是定点，M，D，N均为动点，且点M，D，N共线.

条件①DN=ON，揭示△ODN是等腰三角形，而等腰三角形具有“三线合一”的性质;条件②ON=1，O是定点，揭示了动点N到定点O的距离为定值1，即动点N的轨迹是一个圆，其方程为x2+y2=1;条件③MN=3，结合DN=ON=1，得知点D是线段MN的接近点N的三等分点.综合上述对已知信息的思维分析可知，动点N的轨迹是一个圆，点N的运动主导着点D的运动，自然决定着点M的变化.因此，欲求点M的轨迹曲线C的方程，势必运用几何法或者相关点转移法.

3 第1)小题的求解思路

我们能否判断出曲线C的类型呢?试想，当点N在x轴的负半轴上时，显然点M的坐标是(－4，0);当点N在x轴的正半轴上时，点M的坐标是(4，0);当点N在y轴的负半轴上时，点M的坐标是(2，0);当点N在x轴的正半轴上时，点M的坐标是(－2，0).据此可推测曲线C的轨迹是椭圆，且a=4，b=2，曲线C的方程为.这样一来，解题目标自然变成了围绕猜测结果构建一个严谨又无失分点的解题过程.运用数学问题中的普遍与特殊的关系，通过对特殊情况的研究来判断或者猜测一般规律，这正是一般化与特殊化思想的应用.

解法2设点 D(t，0)，(其中|t|≤2)，M(x，y)，依题意，，且.

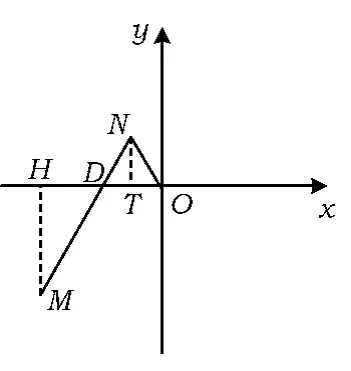
图3

过点N，M分别作x轴的垂线，垂足分别为T，H.由平面几何知识，可得

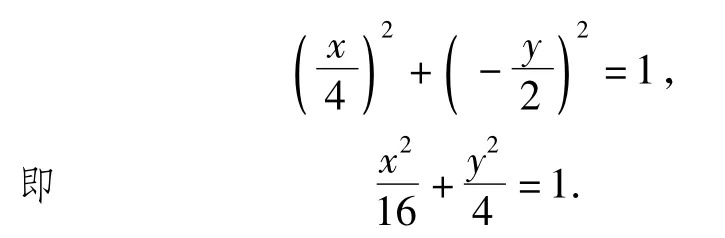
本题的作图工具与椭圆第一定义的作图工具不同，是椭圆的又一种尺规作图.圆锥曲线的尺规作图是值得我们深入研究的经久不衰的课题.

4 第2)小题的求解思路

运用极限的思想，试想:当椭圆的切线趋近于平行已知的任意一条定直线时，三角形的面积自然趋向于无穷大，因此△OPQ的面积不可能有最大值.又

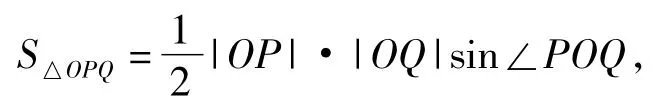
而sin∠POQ是定值，从而△OPQ的面积取决于|OP|·|OQ|.结合椭圆的对称性自然猜想到当|OP|=|OQ|时，S△OPQ取得最小值，此时直线l与坐标轴平行，最小值是ab.

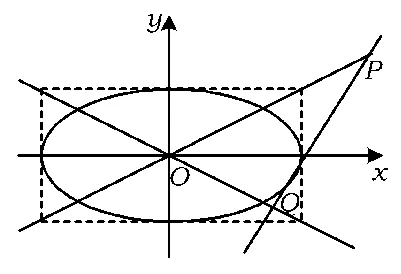
图4

解法11)当直线l的斜率不存在时，直线l为x= 4或x=－4，都有

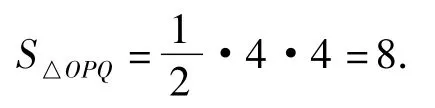
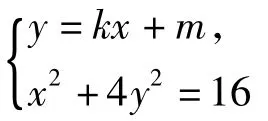
消去y，可得 (4k2+1)x2+8mkx+4m2－16=0.

因为直线l总与椭圆C有且只有1个公共点，所以

综合1)，2)可知，当直线l与椭圆C在2个顶点处相切时，△OPQ的面积取得最小值8.

评注若直线l与曲线C:f(x，y)=0相切于点(x0，y0)，则直线l也可以应用隐函数的导数求解.如C:边求导得，即，则点(x0，y0)处的切线方程为

解法2设直线l与椭圆C相切于点(x0，y0)，则直线l可表示为

评注若求出△ABC的顶点坐标A(x1，y1)，B(x2，y2)，C(x3，y3)，也可以应用行列式求解△ABC的面积，即.本题中△OPQ的面积

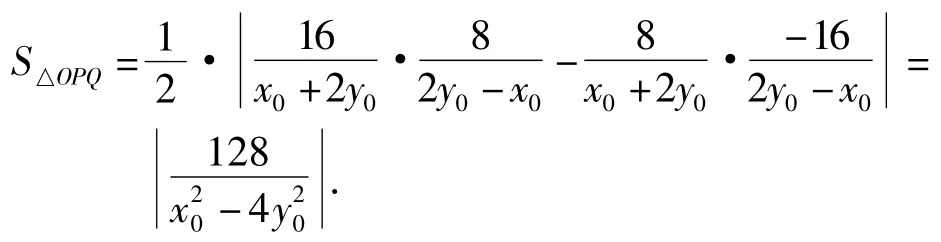
5 第2)小题的拓展

反思1本题的结论是否具有一般性呢?

引申1若直线l与椭圆C:相切于点(x0，y0)，动直线l与2条定直线l1:bx－ay=0和 l2:bx+ay=0分别交于点 P，Q，则，其最小值是ab.

反思2本题的结论是否可以类比到双曲线呢?

引申2若直线l与双曲线C:相切于点(x0，y0)，动直线l与2条定直线l1:bx－ay=0和l2:bx+ay=0分别交于点P，Q，则S△OPQ是定值，且该定值为ab.

问题解决的策略是多种多样的，既取决于对问题题设信息的理解与认识，又取决于解题主体的知识积累与经验.解题的机智往往就在于你是否真正透彻地熟悉信息、理解信息、运用信息，能否对信息进行捕捉和储备知识及方法进行有序组合，能否抓住问题的数学本质，而对问题本质的发现还在于我们对问题信息的多角度审视和挖掘.

为此，在平时的复习教学中，教师要有意识地引导学生注重审题，学会分析，善于捕捉题设条件的信息加以透析，关注解题后的对问题本质的挖掘和透视，提升解题的驱动力.