运用定义巧解题——探讨一类椭圆离心率的通性通法

●许昌满 (嘉兴高级中学 浙江嘉兴 314031)

运用定义巧解题
——探讨一类椭圆离心率的通性通法

●许昌满 (嘉兴高级中学 浙江嘉兴 314031)

1 问题的提出

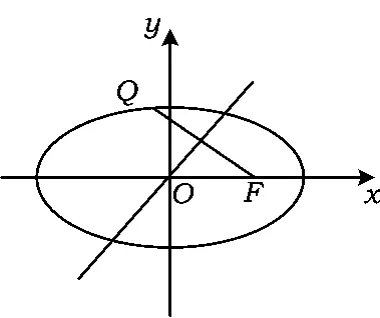
图1

(2015年浙江省数学高考文科试题第15题)

这是一道求椭圆离心率的问题，命题遵循了浙江省数学高考“条件简洁、问题清楚”的风格，但考生普遍感觉“入手容易，计算难”.其实，这涉及到3个方面:第一，对题意的理解与等价转化;第二，对解法的选择和优化;第三，对计算能力的要求.本文试图从椭圆离心率的有关知识要点出发，以一道浙江省会考题为引例，通过变式和类题，比较解法的优劣，选择与优化，并进行拓展，最后提出几点教学思考，以期抛砖引玉.

2 分析与解决

2.1 知识要点分析

1)椭圆的定义:平面内与2个定点F1，F2的距离之和等于常数(大于|F1F2|)的点的轨迹叫做椭圆.反之，椭圆上任意一点P，到2个定点F1，F2的距离为|PF1|，|PF2|，均有|PF1|+|PF2|= 2a(其中2a＞|F1F2|).

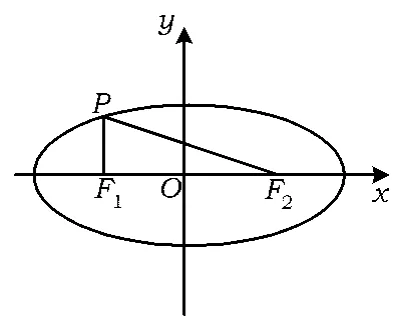
图2

4)椭圆离心率的几何意义可以理解为:在椭圆长轴长不变的前提下，2个焦点离开中心的程度.离心率越大，椭圆越扁;反之，离心率越小，椭圆越接近于圆.

5)与椭圆离心率相关的常见题型:求e的值，求e的范围.

2.2 问题的解决

2.2.1 从一个引例说起

引例设椭圆(其中a＞b＞0)的左、右焦点分别为F1，F2，过点F1作x轴的垂线交椭圆于点P，若，则椭圆的离心率为 ( )

解法 1由 PF1⊥F1F2，， |F1F2|=2c，得，故.因点P在椭圆上，代入椭圆的方程并化简得

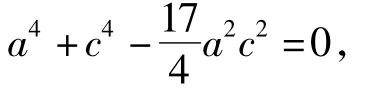
解法2由题意可知

因点P在椭圆上，由椭圆定义

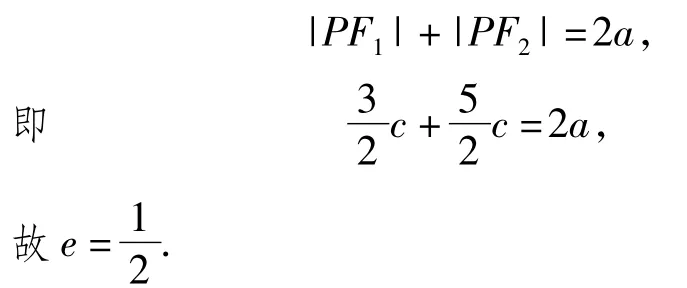
评析一般地，求椭圆离心率的值，其实就是要寻找或建立一个含有a，b，c或其中任意2个的方程，结合b2=a2－c2，解得c和a的值或者其比的值.解法1先求出点P的坐标，再代入椭圆的方程，得到含有c与a的方程.解法2先算出|PF1|，|PF2|的值，再利用椭圆的定义，得到含有c与a的方程，直接求出离心率.很显然，解法2的计算量较小，得到的方程也更为简洁.

2.2.2 变式与类题

变式1如图3，设椭圆(其中a＞b＞0)的左焦点为F1，O为坐标原点，P为椭圆上一点，若△PF1O为等边三角形，则椭圆的离心率为______.

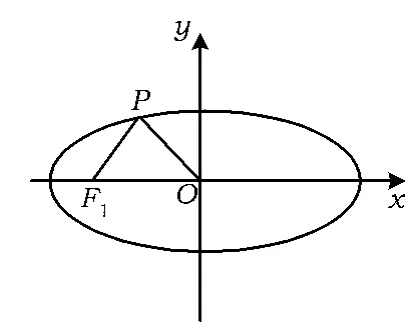
图3

解法1由题意，不难得出，代入椭圆的方程并化简得

解法2设椭圆右焦点为F2，联结PF2，易得.由椭圆定义得，故.

评析变式1中没有出现右焦点，解法2创设了右焦点，构造一个以|PF1|，|PF2|为边的△PF1F2，算出|PF1|，|PF2|，利用椭圆定义，便直接建立了a与c的方程，简化了计算，较解法1更胜一筹.

类似题1已知等腰直角△ABC的斜边为AB，以点为A中心、点B为焦点作椭圆，若直角顶点C在该椭圆上，则椭圆的离心率为______.

(2011年浙江省名校联盟卷文科第15题)

变式2如图4，椭圆(其中a＞b＞0)的左、右焦点分别为F1，F2，过点F1作x轴的垂线交椭圆于点P，Q.若∠PF2Q为锐角，则椭圆的离心率的取值范围为______.

图4

解法1由题意，设点P的坐标为P(－c，yp)，由点P在椭圆上，代入椭圆的方程，可解得，即.因为∠PF2Q为锐角，所以∠PF2F1＜45°，从而|PF1|＜|F1F2|，即，消去b2，得a2－c2＜ 2ac，解得或(舍去)，故.

解法 2退一步，当∠PF2Q为直角时，有∠PF2F1=45°，由题意容易算出|PF1|=2c，，根据椭圆定义，得，从而，故当∠PF2Q为锐角时，椭圆变扁，离心率随之变大，因此.

评析变式1到变式2，条件由等边三角形到锐角三角形，由角度确定到角度有范围，问题也由求离心率的值到求范围.因此，解题策略也由构建方程到构建不等式.解法1根据角之间的不等关系，建立边之间的不等关系(大角对大边)，从而建立一个关于a，b，c的不等式，求出e的范围.解法2看似巧妙，实则为等价转化，“以退为进”.根据方程与不等式、直角与锐角间的辩证关系，先求出直角条件下椭圆的离心率，再结合椭圆离心率的几何意义，便间接求出了锐角条件下离心率的范围.

类似题2椭圆(其中a＞b＞0)的焦点为F1，F2.若椭圆上存在点P，使△PF1F2是以PF1为底边的等腰三角形，则椭圆离心率的取值范围是

( )

(2014年浙江省数学学考试题第23题)

2.2.3 2种方法的比较

有了以上的准备，对于例1，常见的有如下2种解法.

解法1设F(c，0)关于直线的对称点为Q(m，n)，由题意有

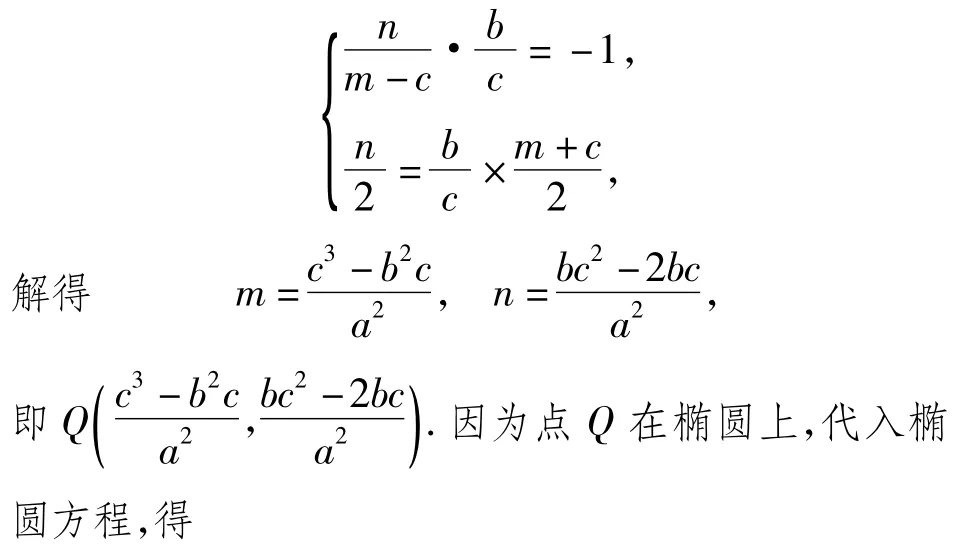
解法2如图5，设椭圆的左焦点为 F1(－c，0)，联结QF1.设QF与直线交于点M，由题意知M为线段QF的中点，且OM⊥QF.又O为线段F1F的中点，故OM为△FF1Q的中位线.在Rt△OMF中，，从而

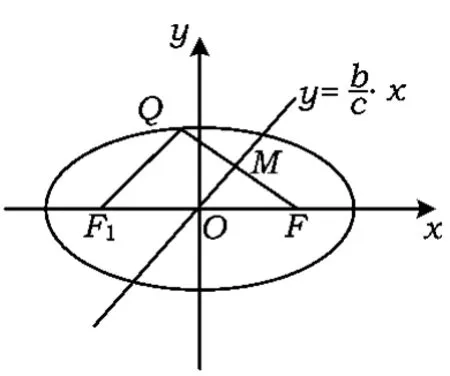
图5

评析解法1根据题意的条件，直接转化(我们称之为“直译”)，先利用点关于直线对称的关系，计算得到右焦点的对称点，再通过该点在椭圆上，代入方程，化简得到关于a，c的方程，由此计算离心率.但这个计算量是巨大的，对含有字母的运算能力要求较高，笔者通过调查了解及现场演练，发现大部分学生在5分钟、甚至10分钟之内也无法完成.解法2联想到椭圆的定义，创设左焦点F1，联结QF1，这样就如同变式1中的解法2一样，构造了一个以|QF1|，|QF|为边的△QF1F，再将点关于直线对称的条件等价转化(我们称之为“意译”)，得OM为△FF1Q的中位线，算出|QF1|，|QF|，再利用椭圆的定义，问题便得以解决.解法1“起点低、落脚难”，“入手容易、计算难”;解法2等价转化，自然、流畅，计算简洁.因此，解法2应该是我们优先考虑的.

2.3 拓展

综合上述问题，求这样一类椭圆的离心率问题，即条件中给出了椭圆的2个焦点(或只给出1个焦点，此时需要创设另一个焦点)，往往可以构建一个以|PF1|，|PF2|(P为在椭圆上一点)为边的△PF1F2，算出|PF1|，|PF2|，再利用椭圆的定义，通过|PF1|+ |PF2|=2a建立一个含有a，b，c或其中任意2个的关系式，从而算出离心率的值或范围，这是我们解决上述问题应优先考虑的通性通法.其实，这种通性通法还可以拓展到双曲线的离心率问题和椭圆、双曲线的综合离心率问题中，举例如下(由于篇幅有限，具体解法在此不再赘述).

1.如图6，F1和F2分别是双曲线(其中a＞0，b＞0)的2个焦点，A和B是以O为圆心、以|OF1|为半径的圆与该双曲线左支的2个交点，且△F2AB是等边三角形，则双曲线的离心率为 ( )

(2007年安徽省数学高考理科试题第9题)

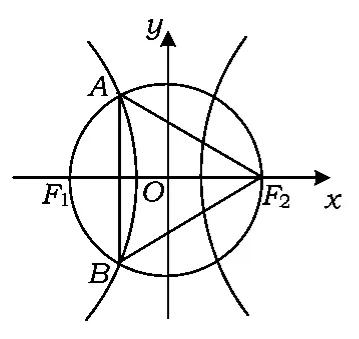
图6

图7

2.如图7，F1，F2是椭圆C1:与双曲线C2的公共焦点，A，B分别是C1，C2在第二、四象限的公共点.若四边形AF1BF2为矩形，则C2的离心率是

( )

(2013年浙江省数学高考文科试题第9题)

(2013年浙江省嘉兴市二模试题理科第8题)

3 几点思考

3.1 关于数学概念的教学

李邦河院士曾说“数学是玩概念的”.概念是一切数学活动的基础，若概念不清就无法进一步开展其他数学活动.因此，数学教师要特别重视概念教学的研究，注重数学概念产生的背景，以及它的发生、发展和应用，注重数学过程的体验，注重对数学本质的理解与感悟.

比如在上“椭圆及其标准方程”时，教师可让学生自己动手制作工具并演示，从中体验椭圆的形成过程.教师再配上几何画板动态演示，加深学生的感观.又如在上“双曲线及其标准方程”时，教师可以和学生一起探究，为什么初中所学的方程所对应的图像也叫双曲线，它和高中所学的双曲线(其中a＞0，b＞0)有什么区别和联系，它的中心在哪里，实轴在哪里，焦点又在哪里?这样，在学生的最近发展区提出问题、研究概念，会更亲切、自然而有效，同时还可以培养学生学习数学的兴趣，激发求知的欲望.

3.2 关于解题方法的选择、优化与认识

一道数学试题，如从不同的背景和视角出发，可以有不同的解法.有些教师在日常教学时，过分地追求自己的“一题多解”，而忽视了学生的“主体参与”.特别是一些公开课，看似“热闹”的课堂，其实是教师一个人展示“高难动作”的“绝活表演”.一些技巧性较强的“秒杀”法，学生“拍手叫绝”，轮到自己做时，由于缺乏独立认识和思考，便会出现“邯郸学步”的尴尬境况.

在例题或习题教学中，我们应鼓励学生积极参与，让“百花齐放、百家争鸣”.但更要引导学生从中提炼、总结出最初、最基本的数学概念，最自然、最优化的解题方法.通过对一道题目的深入研究，透过现象抓住本质，找出规律，以逐步达到“做一题，会一类;用一法，解多题”的效果.这种“大众化”的通性通法，不仅有利于学生求同思维的发展、聚敛思维的提升，也是新课改理念下，摆脱“题海战术”、减轻学生负担所倡导的.

在解题教学中，还应注重对解题方法本质的认识.比如，在引例中，点P在椭圆上，有2种处理的策略.解法2利用椭圆的定义(其实是将椭圆的定义当作椭圆的性质在用，即椭圆上任意一点P，到其2个焦点F1，F2的距离之和|PF1|+|PF2|均为2a);解法1将点P的坐标代入椭圆的方程，其实也是在利用椭圆的定义(因为椭圆的方程就是根据其定义推导出来的).

3.3 关于计算能力的培养

《课程标准》中提到的“5种能力”，就包括运算求解能力.在“圆锥曲线”的教学中，应特别强调对学生计算能力的培养.我们应将这种训练和培养融入到每一节课中.比如，在上“椭圆及其标准方程”时，让学生自己动手推导椭圆的标准方程;在上“双曲线及其标准方程”时，要“舍得”拿出时间让学生自己动手推导(有部分教师认为在前面已经推导过椭圆的标准方程，再在课堂上给学生推导双曲线的标准方程，是“重复劳动”、“浪费时间”.殊不知，这是培养学生字母运算能力的大好时机).虽然浙江省数学高考命题重视“多想一点，少算一点”，但很多学生却往往“失误”在一些最基本的运算上.初中的课改，将计算器引入课堂，但高考却不能将计算器带入试场.因此培养学生的计算能力，需要从学习中的每一个细节抓起.

3.4 关于数学思想的感悟

解题教学不要仅仅停留在某种“解题术”的训练上，还要引导学生及时地提取并掌握其中的通性通法.更重要的是，还要发展学生感悟其中所蕴含的数学思想方法的意识.比如，变式2的解法2和例1的解法2中所蕴含的等价转化思想、数形结合思想等等.学生这种数学思想的树立，需要教师长期、有意识地营造氛围，无意识地熏陶，让他们自然地被感染和领悟，而非我们偶尔那几句“苍白”的“说教”或“呐喊”.

［1］中华人民共和国教育部.普通高中数学课课程标准(实验)［M］.北京:人民教育出版社，2004.

［2］许昌满.一道数学高考试题的多元透析［J］.中学教研(数学)，2014(12):36-39.

［3］谢全苗.数学解题教学中要辩证地看待“通法”与“巧法”［J］.数学通报，2001(6):33-34.