远看成岭侧成峰——2015年浙江省数学高考数列题阅卷体会

●曹 毅 (浙江师范大学附属中学 浙江金华 321004)

远看成岭侧成峰
——2015年浙江省数学高考数列题阅卷体会

●曹 毅 (浙江师范大学附属中学 浙江金华 321004)

在数学高考改革承上启下的关键一年，高考试卷在内容和形式上的每个变化都是新政策的应用与实践.2011年才回归高考的数列，在此次高考中以文科第2道大题与理科压轴题的形式出现，不禁让人感觉意料之外，情理之中.笔者有幸参加了2015年浙江省数学高考阅卷，下面就文科第17题进行分析，并对照历年高考数列题，谈谈反思与体会.

题目已知数列{an}和{bn}满足a1=2，b1= 1，an+1=2an，(其中n∈N*).

1)求an及bn;

2)记数列{anbn}的前n项和为Tn，求Tn.

(2015年浙江省数学高考文科试题第17题)

1 试题剖析

1.1 命题意图

本题紧扣高考考试说明，第1)小题为8分，考查等比数列的通项公式与累乘法;第2)小题为7分，考查错位相减法与计算能力.

1.2 解法赏析

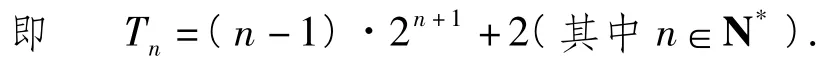
本题的关键点:求出数列的通项公式;错位相减法.

1.3 评分策略

本题的评分体现出高考改卷的2个维度:注重方法，解题思想一定要到位;强调计算，关键结论一定要算对.

第1)小题中，数列{an}和{bn}的通项公式各4分，其中过程与结果分别占2分.第2)小题中，对于错位相减法的评分，只要考生将Tn乘以2或者是，体现出错位相减法的意识就给2分.就算此前考生在求数列通项出现错误，也不会影响本步骤得分.

对于最后的结论，Tn只要满足如下任一种形式即可:

这些都视为正确答案，充分体现了人文关怀.

2 错误解析

2.1 本题得分情况

本题的平均得分为9.59，去除0分试卷后平均得分为10.58.从阅卷情况看，本题的得分普遍在8分以上，且错误较为集中.

2.2 考生常见错误点

第1)小题:

②化简错误:累乘后，得到错误的通项公式，例如bn=2n，bn=n－1等.

对于第1)小题，错误主要集中在求{bn}的通项公式上，其中以概念错误为主，很多考生看到这个式子后，没有联想到“累乘法”，而是乱写一通甚至空白.

第2)小题:

①使用错位相减法时发生错误:

第1)小题算错，得到{anbn}根本不是差比数列，结果还是使用了错位相减法，没有理解方法的本质;

乘上错误的公比，例如4Tn;

最后一项系数错误，如:

2Tn=22+2·23+…+(n+1)·2n+1;

最后一项符号错误，如:

Tn－2Tn=2+22+23+…+2n+n·2n+1.

②计算错误:将

Tn－2Tn=2+22+23+…+2n－n·2n+1

化到最后结果时出现的各种错误.

考生答题中出现千奇百怪的错误，其实质是因为没有理解方法的本质，既不知道使用方法的前提，也不知道方法的作用.例如，错位相减是为了让中间各项的系数变成等差数列的公差，再用等比数列求和公式求解，而部分考生只是记得老师说过要在Tn前乘上一个数.这种机械式记忆的学习方法是文科考生学习数学时最忌讳的.

2.3 得分技巧

①第1)小题不能做错，如果数列{an}和{bn}求解发生错误，第2)小题就只有错位相减法这步得2分，那么此题的得分不会超过8分.

②体现解题思想的关键步骤一定要写，例如Tn－2Tn=2+22+23+…+2n－n·2n+1，这步不仅体现了错位相减法的思想，从中也可以看出数列{an}和{bn}通项求解是否正确，那么这位考生的得分不会低于12分.

3 远看成岭侧成峰，与近3年文科数列大题进行比较

1)知识层面:笔者研究了近3年的高考数列题.第1)小题主要考概念:出现的高频考点为求等差、等比数列的通项与求和;第2)小题主要考方法技巧的掌握:错位相减法、绝对值求和、利用项数的整数性质等教学中常见的方法与性质都是考点.解决这类问题，要求考生理解掌握数列双基.错位相减法在2012年和2015年的浙江省数学高考试题中都有出现.

2)能力层面:近3年浙江省数学高考严格按照考试说明，强调“能力立意”，即考生使用数列知识与技法的能力，看重通性通法与计算能力.如果考生只是套用在文科科目中以记背为主的学习方法，学习数学时只能是事倍功半，遇到题目稍有变化，就会感觉力不从心.

纵观近3年浙江省数学高考文科试题，第2道大题始终是数列题，且对于其方法技能的考查都较为单一，并不繁杂，这说明数列在高考文科数学中以考查双基为主.

4 教学启示

从阅卷情况看，学生的双基掌握得并不理想.很多学生在做题时概念模糊，使用解题方法时漏洞百出，计算也错误连连.针对本题所反映的问题与考查意图，建议在教学中应注意以下2个方面:

4.1 夯实基础，强调双基

对于文科学生来说，教师应指导其重视基础题的训练，规范解题过程，抓牢关键得分点，对于计算的准确性更要精益求精.不要一味地训练难题、怪题、偏题，不要盲目地追求解题技法的华丽性，否则在考试中很容易因为计算不仔细而出错.

4.2 调整课堂结构，优化复习体系

对于教师而言，制定正确的高三复习策略，数列复习课不要太难、太深，容量不要过大.改变课堂结构，改“教师灌输为主”为“以学生思考为主”，让学生发现数学的本质，如复习等差、等比数列求通项时，引导学生提炼出“累加法”与“累乘法”;在复习等比数列求和时，引导学生提炼出“错位相减法”.增加课堂上学生练习的时间，让学生多上台说题板书，训练学生解题的规范性与计算的准确性.

总之，2015年浙江省数学高考试卷向我们传递出:高中数学是玩“概念”的，应该重视概念的理解，重视通性通法，通过玩“概念”培养学生的思维能力与计算能力，只有夯实基础，才能无往不胜.