等效原理与双生子问题

2015-07-02邵成刚

物理与工程 2015年2期

徐椰邵成刚

（华中科技大学物理学院，基本物理量测量教育部重点实验室，湖北武汉 430074）

众所周知，引力场的钟慢效应、引力红移效应及双生子问题，长久以来在教学中都是难以清楚解释的物理现象，对这些效应的认识众说纷纭.清晰地阐明这些问题，无论是对于更深层次的学术讨论还是教学本身都是非常重要的[1-3].

由狭义相对论得知在惯性系中匀速运动的钟要比静止在惯性系中的钟走得慢，而非惯性系中的物理规律也可以通过一定的坐标变换，在狭义相对论的框架下得到很好的描述.但是狭义相对论却不涉及有关引力的讨论，故由引力引起的一系列效应，如引力场的钟慢效应和引力红移效应，都不能通过狭义相对论来解释.然而，在量子理论出现以前，爱因斯坦在经典波动理论范畴下，巧妙地利用等效原理，将一个匀加速系统和一个均匀引力场等效起来，成功地推导出了引力场的钟慢效应和引力红移效应，进而进一步建立了描述引力现象的全新理论——广义相对论.本文借助于等效原理重新论证了引力场的这两个效应，并进一步给出了双生子问题在狭义相对论下的解释，辅助学生更深入地理解等效原理，加深对广义相对论的认识.

1 等效原理

广义相对论的基石是爱因斯坦等效原理：任何物理实验——力学的、电磁的和其他的实验都不能区分引力和惯性力的效果.

做这样一个思想实验，我们可以想象一个与外界完全隔绝的封闭舱，舱内的人从高处释放一个物体并观察到物体自由下落，他可以认为自己的密封舱是静止的，物体的自由下落归因于密封舱下面的一个均匀引力场（例如相对于地球向心引力场，这个足够小的密封舱内的引力场可以看作是均匀的）；当然他也可以认为他的舱在太空中做匀加速运动，物体的自由下落归因于加速度引起的惯性力.密封舱中的人无法通过任何物理实验分辨出他自己是处于加速状态，还是处于一个均匀引力场中.不受引力的加速系等效于均匀引力场中的惯性系，发生在一个匀加速系统中的物理过程，会毫无变化地发生在一个引力加速度等于匀加速系统加速度的均匀引力场中.在某个星球表面附近自由下落的足够小的密封舱内，空间中的引力与惯性力近似完全抵消，任何力学实验、电磁学实验都不会受这个密封舱的运动状态影响，自由下落的局域参考系是近似的局域惯性系，引力和惯性力在物理效果上完全没有区别，这就是爱因斯坦等效原理.

2 引力的钟慢效应

我们借助于一个匀加速运动的密封舱模型，从等效原理推导出引力场的时钟变慢效应.

2.1 匀加速运动的密封舱

首先来看一个密封舱模型：足够小的密封舱在空间某处不受引力影响，舱以均匀加速度g向上做匀加速运动，舱内A、B点间的距离为h，A、B两处分别有两个完全相同的钟，两个时钟的计时机制和计时速率完全相同.B处有一个发射脉冲的装置，该装置与B钟相对应，如每经历Δτ时间间隔发射一次；A处有一个接受脉冲的装置.密封舱从v＝0开始加速，不失一般性地假设在所讨论的时间段内，密封舱的最终速度v＝gt≪c且g＝const，进而整个过程密封舱长度h的收缩效应可忽略.整个实验的过程如图1所述.

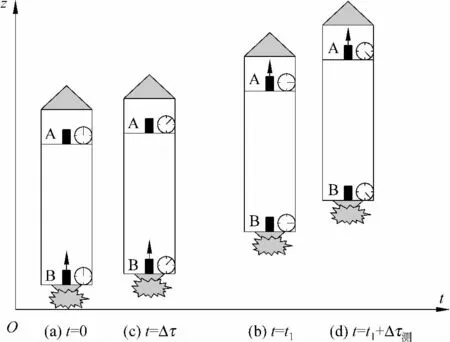
图1 密封舱匀加速运动，A钟与B钟速率相同

图1中，从左到右依次为（a）、（c）、（b）、（d）4个时间点，按照事件发生顺序排列，（a）、（b）和（c）、（d）分别为两个脉冲的传播过程：

（a）t＝0时刻，B朝 A发射出脉冲1，B的钟表上显示“0”，B钟开始计时；

（b）t＝t1时刻，A接受到这个脉冲，A的钟表上显示“t1”，作为对钟过程可将A钟的显示调为“0”；

（c）t＝Δτ时刻，B又朝A发射脉冲2，B的钟表上显示的时间就是“Δτ”，为B经历的固有时，和B钟上显示的一致；

（d）t＝t1＋Δτ测时刻，A接收到B发射的第二个脉冲信号.距离A上次接收到脉冲信号的时间间隔为Δτ测，注意这里的Δτ测是A观测到的时间差，就是以A钟为标准记录的时间差，注意A钟和B钟完全一致；图2简洁地表示了以上4个事件发生的先后顺序，在惯性系中看来，Δτ测≠Δτ.

下面计算A观测到的时间差Δτ测和B钟的时间差Δτ的关系：根据A、B的运动规律，在惯性系中看来，以刚开始加速B的位置为坐标原点，A、B的位置可以表示为

（a）、（b）过程：

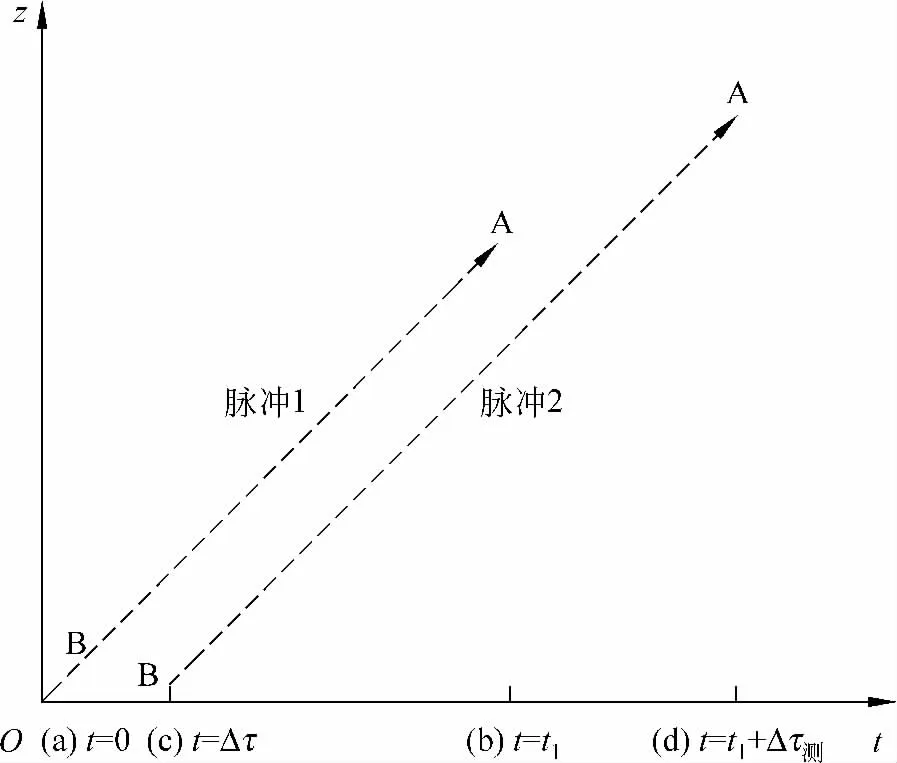
图2 脉冲1与脉冲2的世界线

（c）、（d）过程：

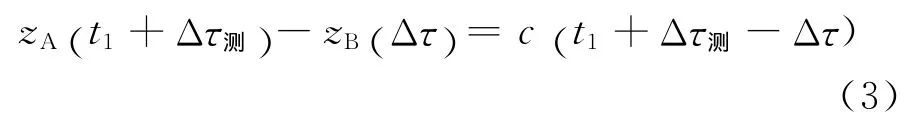
由式（1）～式（3），忽略时间差平方的二阶小量可得

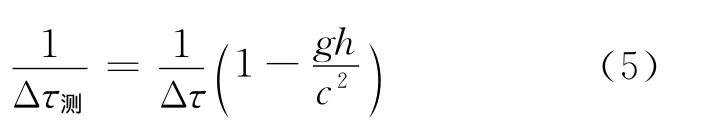
可以看出，Δτ测＞Δτ，当B发射两个脉冲信号的时间间隔为Δτ（B钟读出）时，A接收到两个脉冲信号之间的时间间隔为Δτ测，A认为这个时间间隔变大了，图3清晰地表示出整个事件发生的流程（图中A和B接收到的脉冲用记数“1”“2”“3”来表示）.

图3 匀加速系中，A钟与B钟的比对

可以看出，对A来说，本该在记数“2”时就接收到脉冲2的，却在其记数了“2”后某个时间才接收到脉冲信号，A等了Δτ测的时间才接收到脉冲信号，在A看来是B发射的脉冲2走过的距离比脉冲1大（因为此时A认为自己所处的密封舱在做匀加速运动），所以A等了Δτ测的时间才接收到信号.

现在可以得出结论，在这样一个匀加速系统中，A观测到B发射两个脉冲的时间间隔要比B自己观测到的这个时间间隔要大，由于不是A钟和B钟的影响造成的这种观测的不一致，故A给出的结论是脉冲2比脉冲1走过的距离长，导致Δτ测＞Δτ.

2.2 均匀引力场

同样可以让2.1节中的系统静止于一个均匀的引力场中，如图4所示.不失一般性地使密封舱的尺度足够小以使舱中的引力场相对于某个星球的向心引力场是均匀的.在这个密封舱中同样由B发射脉冲给A，整个物理过程同前面完全一致，只是这是发生在一个均匀引力场中.

根据第1节给出的爱因斯坦等效原理，不受引力作用的加速系等效于均匀引力场中的惯性系，密封舱中的人无法通过任何物理实验分辨出自己是处于加速状态，还是处于一个均匀引力场中.那么密封舱中的A、B两人完全不能发觉2.2节和2.1节中的系统有任何差别，他们还是同2.1节中一样两次发射、接受脉冲，他们同样会记录发射或接受的时间并测到与上面完全相同的时间间隔.为了与上述2.1节情况区别，我们用ΔτA和ΔτB来表示均匀引力场中密封舱内A、B观测到的两次脉冲之间的时间间隔，也就是他们各自的固有时.根据2.1节中（5）式我们可以得到

同样有ΔτA＞ΔτB，只是此时的结果是在一个均匀引力场中得到的.那么此时A该如何来解释这个测量结果呢？系统没有加速运动，脉冲2和脉冲1走过的距离完全相同，那么2.1节中的解释当然不可行，对A来说，他静止于均匀引力场中，然后观测到两次脉冲之间的时间间隔大于B观测到的结果，可以给出以下两种可能的解释：

（1）A认为自己的钟和B钟都没有问题，还是完全相同的两个钟，由于系统处在引力场中，故脉冲会受到引力的影响，使得脉冲2较脉冲1花费更多的时间传播到A，导致ΔτA＞ΔτB；

（2）A认为自己的钟没有问题，而B发射脉冲是根据B钟上面的一个单位时间来发射的，但是A确实观测到B发射两次脉冲之间的时间间隔小于自己接受到的两次脉冲之间的时间间隔，那么A只能认为B钟变慢了．

对于解释（1），A自己便可反驳这样的解释，因为如果是引力影响了光脉冲的传播，那么这个作为背景的引力对任何脉冲的影响在任何时候都是相同的，不会因为脉冲1和脉冲2发射时间的不同而不同，那么脉冲1与脉冲2将完全没有差别，也就不可能会有ΔτA＞ΔτB了，所以解释（1）是无效的解释．

对于解释（2），即A认为B钟变慢了，这是唯一可能的解释．那么是什么原因导致B钟变慢了呢？自然地，我们可以认为是引力导致了B钟变慢，因为区别于2．1节，这里唯一的影响因素就是引力．至此可以得出结论：引力场使时钟变慢．

由2．1节、2．2节便清晰地从等效原理推导出了引力的钟慢效应．

3 引力红移

实质上，引力红移效应同引力钟慢效应一样，都可以由等效原理推导出来．这里可以直接从引力使A观测到B钟变慢出发，上述2．2节中的所有装置也是处于在一个均匀引力场中，只是这里让B发射稳定的光波信号给A，这里不失一般性地设B钟发射振荡周期为ΔτB的光波信号；根据2节中的结论，这样的一段光信号被A接受，A需要在A认为的ΔτA的时间段内才能接受完这个信号，A测到的这个信号的周期变为ΔτA，用ν测B和νB分别表示A和B观测到的这个光信号的频率，根据ΔτA和ΔτB的关系式（6）可得

也就是说，B发射频率为νB的光信号，A接收到这个信号并测量发现其值变为ν测B，有ν测B＜νB，产生了“红移”．与前面的讨论一致，A只能够给出引力使B钟走得慢的结论，而A观测到的这个“红移”来源于自己的时钟比B快，故也可以说这个红移现象也是由引力场引起的，由于引力的原因使得A观测到的光频变小，发生引力红移现象．

爱因斯坦给出的引力红移公式可进一步写为

其中，Δφ＝φB-φA，为B到A的引力势差，由A、B间距离h较小近似可得（A离引力源较远，故φA＞φB）：

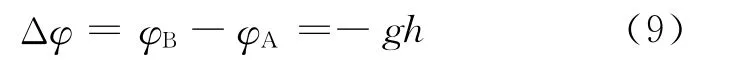
引力红移公式由引力钟慢效应推出，故引力红移和引力的钟慢效应的本质相同，都通过等效原理推出．

当然，量子理论建立起来以后，也可以利用光的粒子性解释引力红移现象，将光波看作一颗颗具有等效质量m＝hω／c2的光子，光子从B运动到A的过程中克服引力做功，能量减小，频率减小，也可得出与式（7）一致的结论，但这样的解释无法与钟慢效应建立联系．

4 双生子问题

双生子问题，指的是这样一种现象：两个年龄相同的人A和B，A留在地球上，B乘坐高速运动的飞船到达另一个星球，然后又飞回来，发现留在地球上的A比自己老（这当然是一个事实）；但是根据运动的相对性，当地球上的A看到B在运动的时候，在B看来，A也是运动的，如果B认为是A乘坐“地球”飞离自己然后又飞回来，按照上面的讨论，那么B就会认为A比自己年轻．同样的分析方法却得到了不同的结果，这便是双生子问题．对于双生子问题，如果在狭义相对论的范围内讨论，需要忽略飞行者反向运动中的减速、加速过程，在B参考系中要用到两个惯性系，通过惯性系之间的坐标变换得到飞行者反向运动时的时间突变．尽管这提供了一个双生子问题的狭义相对论解释，但中间的时间突变过程难以用清晰的物理图像来解释．下面我们将B参考系中的这个时间突变过程对应到减速、加速过程，利用等效原理及2节中的结论，在广义相对论的框架下解释这个问题.

4.1 A参考系

在A参考系中，A停留在地球上，A看见B沿某方向以一个极大的加速度加速离开自己，飞行了h后又飞回来，不失一般性地假设B的加速过程相对于整个长途旅行来说极短.B的速度本来是v（t），是时间t的函数，但是这里可以将其看作常速度v直接计算B的时间膨胀，这个假设对后面的讨论没有影响.用图5中的世界线来描述整个过程.

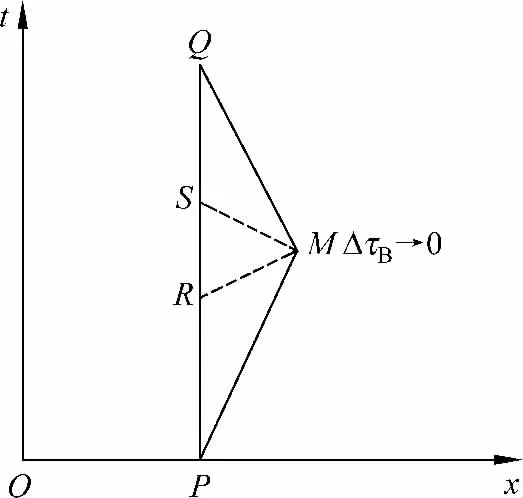
图5 A参考系

A参考系中，PRSQ是A的世界线，PMQ线是B的世界线.停留在地球上的A看B以速度v离开又回来，A、B的固有时分别表示为τA和τB，我们可以得到

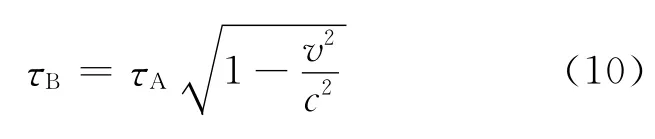
可以看出最后两人再次相遇时，B所经历的时间小于A所经历的时间，B比A年轻.

这里需要着重指出，对于A参考系而言，这是一个惯性系.当飞船飞到最远端处开始减速并最后转向时（图5中的M点），这一段过程在惯性系中的坐标时为Δt，而时钟B的输出量是作为观测量的固有时 ΔτB，两者的关系为当Δt趋于零时，ΔτB也可以忽略.这也是狭义相对论中的加速时钟原理ACP（accelerated-clock principle）[4]，即惯性系中运动时钟的输出与其加速度无关，只依赖于其运动速度.因此，在A参考系中，A自己并没有经历加速与减速过程，也不需考虑飞船的加速度及其涉及的等效引力场问题.但对于参考系B而言，B自己是经历了加速与减速过程的，这是一个非惯性系问题，下面我们对此详细分析.

4.2 B参考系

首先，在B参考系中给出狭义相对论范畴内的讨论[5].可以直接利用图5来说明B参考系下每个阶段A、B固有时的关系.这里需要区分B参考系下A飞离B和飞向B的两个惯性系，考虑同时的相对性.如图5所示，辅助线MR表示在A飞离B时的惯性系下M与R同时，MS表示在A飞向B时的惯性系下M与S同时，而A反向时从第一个惯性系变换到第二个惯性系有一个时间突变，即为图中的RS阶段，这个阶段A的固有时为而对应B世界线上M点处B的固有时ΔτB→0.表1中给出狭义相对论下B参考系中各个阶段A、B固有时的关系，可以得到与4.1节中式（10）一致的结论.

表1 B参考系中各阶段固有时关系

下面我们在B参考系中将上述狭义相对论下的讨论对应到广义相对论下的讨论.图6的世界线描述广义相对论范畴下的整个过程.图中的P、Q、R、S分别与图5中P、Q、R、S各点对应，辅助线MR、NS表示M与R同时、N与S同时（坐标时同时），A的反向阶段RS对应B的MN阶段.实际情况中，B在MN阶段内减速、加速；狭义相对论下，RS为A的时间突变阶段，MN段B的减速、加速过程被忽略进而坍缩为图5中的M点，但仍有ΔτB→0；广义相对论下，MN段B认为自已处于均匀引力场中，而A在该引力场中与B相距h的地方经历RS段.这里我们仍用τA、τB表示A、B的固有时.

图6 B参考系

①阶段，B的世界线为PM段，对应A的世界线为PR段.B与A在同一个时空点P，A以极大的加速度加速到速度v离开B（与4.1节中一致v近似为常数），加速过程极短可看作发生在时空点P（相当于上文2节中的h＝0），故这个阶段A、B的固有时完全没有差别；加速完成后A进入匀速运动阶段，这个阶段B的固有时是A的固有时是

②阶段，B的世界线为MN段，对应A的世界线为RS段.实际情况中，B在MN阶段内以一个极大的加速度a先减速再加速，由等效原理可知，B也可以认为自己突然处于一个很强的均匀引力场中，而A在这个引力场的高势能处.MN段B的固有时记为ΔτB，由前面的假设可知，相对于τB来说ΔτB→0.根据2节中的讨论，A在该引力场中与B相距h，引力势φB＜φA，故RS阶段A的固有时为：由于h极大这个时间不能忽略.

③阶段，B的世界线为NQ段，对应A的世界线为SQ段.B感受到的引力场消失后，他再次看到A以速度v返回，这个阶段B的固有时同样为A的固有时仍是而后A减速与B相遇的过程可认为发生在同一个时空点Q，与①中的讨论一致，相遇的过程中A、B的固有时不会有任何差异.

表1中给出狭义相对论下每个阶段A、B固有时的关系，与图6对应.

根据上述讨论分别写出A和B的固有时

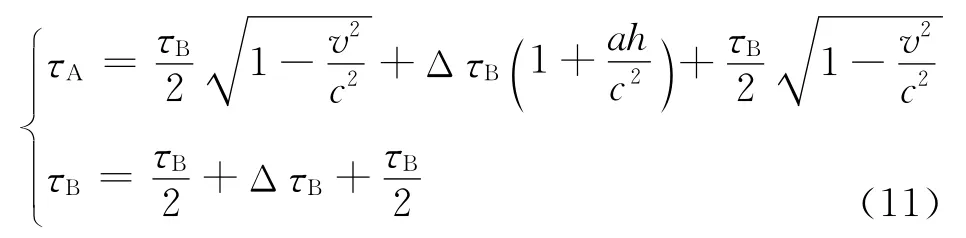
式中的τA、τB是最后A、B再次相遇时各自观测到的时间，式（11）的第二式表示ΔτB相对于τB来说是极小量，实际上B观测到的时间就是B的固有时：τB＝τB，引入ΔτB的原因在于对于τA，ΔτB这一项前面有这个由于h极大而不可忽略的因子，导致计算τA时必须要考虑这一项.

由

注意这里h为B感受到等效引力时所对应的AB间距离，可得

根据式（11）、式（13）可得出

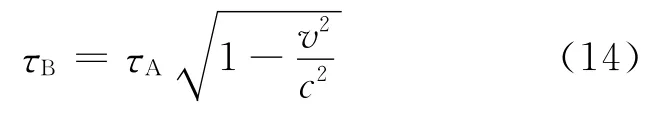
正好与A参考系中得出的式（10）一致，故在B看来，A、B相遇的时候还是B比A年轻，而且年轻的程度和A参考系中一致.由图5、图6及表1，我们将广义相对论下每个阶段与狭义相对论下每个阶段对应起来，分析两个参考系的不对称性，利用等效原理将B的加速度与引力场等效起来，直接计算引力场引起的钟慢效应，得出了与A参考系一致的结论.

这里需要着重指出B参考系与A参考系的区别.对于B参考系而言，当地球或A离开到最远端处开始减速并最后转向时（图6中的RS段），这一段过程对观测者B而言是非惯性系，B自己能强烈感受到自己经历了一个加速与减速的非失重过程.因此B可以等效认为自己与A均处于引力场中.引力场的钟慢效应（B处于低势能处，A处于高势能处，B钟比A钟慢）导致A钟比B钟块，两者之比为当ΔτB→0时，则a→∞，但两者乘积ΔτBa→const，因此ΔτA不能忽略，在B参考系中应该考虑飞船反向加速所对应的引力效应，这一过程对应的ΔτA＝（见表1），它起决定作用.

我们也可以给出最简单的数学几何解释，利用闵可夫斯基空间中测地线的性质来理解双生子问题[6]，四维时空中世界线的长度是绝对的，不论在哪个参考系、哪个坐标系中，对任何观察者而言世界线的长度都不变，即守恒，既然A参考系中A的世界线是测地线，长度取极大值，那么A经历的时间自然最长，在A、B参考系中讨论得出的结果一定都是A比B老.