简谐波势能的一种简明推导

周 越 张国锋

（1北京林业大学理学院，北京 100083；2北京航空航天大学物理科学与核能工程学院，北京 100191）

简谐波的能量可分为介质各质元的振动动能和介质因发生弹性形变而具有的势能两部分.其中质元的振动动能易于从波动方程导出；而弹性势能的计算则相对复杂，较完整的讨论需利用杨氏模量、切变模量等连续介质力学方面的背景知识[1]，这些内容在少学时的普通物理课程中一般很少涉及.故在论证介质中动能密度和势能密度相等时，很多教材只是用示意图来定性说明振动速度大的质元同时亦具有较大的形变，或者直接用“可以证明”略过[2].如能用基本的力学知识说明两者定量相等，有助于加深学生对问题的理解.文献[3]利用动能和势能密度在一个周期内平均值相等结合两者同步调增减进行论证，但由此断言两者的瞬时值亦相同略嫌证据不足.文献[4]以在绳中传播的横波为例给出了一种定量的证明，但在证明过程中需使用波形在任何一点斜率极小的近似条件，相当于在绳上传播的横波振幅必须远小于其波长，这样引入了不必要的附加条件，且容易给学生留下简谐波的动能和势能密度只在小振幅下才近似相等的印象.本文同样基于在细绳中传播的简谐波，给出一种只需较少背景知识的推导方法，在弹性限度内无需对振幅的大小作特别限制，且可以同时得到波速和绳两端张力的关系.

1 质元的动能

首先考虑一列在细绳中传播的简谐横波，如果细绳在起振之前与x轴相重合，波动方程可以一般地表示为[2]

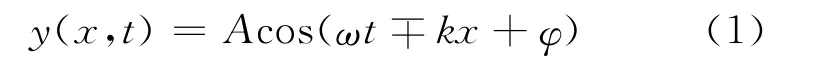
则在细绳上振动速度的分布为

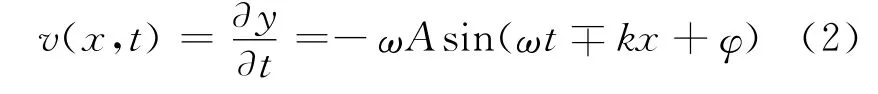
考虑细绳上在x轴投影长度为dx的一段质元，如细绳的线密度为ρ（未起振时的线密度），则该质元的振动动能为

将式（1）代入式（3）可得

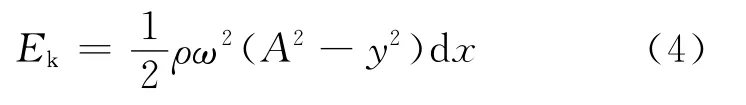
这说明位移大的质元具有较小的振动动能.

2 质元的势能

下面讨论简谐波的势能，因细绳的弹性势能源于质元的形变，与参照系无关，为简便起见，可以在相对波形静止的参照系中讨论.不失一般性，设在此参照系中与波动方程（1）对应的波形方程为

细绳上每个质量为ρdx的质元均在y轴方向作角频率为ω的简谐振动，由简谐振动的性质可知质元所受的线性回复力为[5]

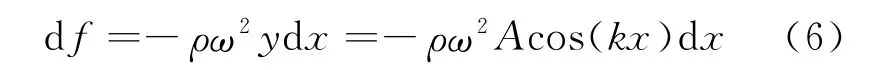
如图1，在细绳上取两点M，N.N在x＝0的正向最大位移处，如M的横坐标为-x，则介于M，N两点间的细绳所受的回复力之和为

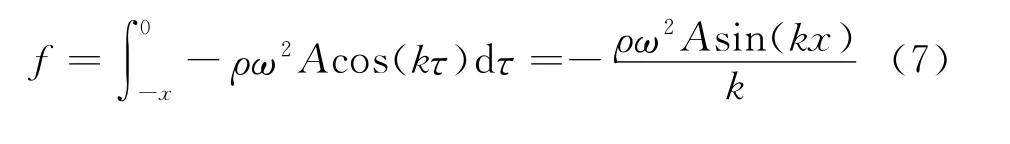
图1 MN段的受力分析

图2 M点拉力的分解

在细绳内不存在法向应力，而N点的切线平行于x轴，因此f来源于M点的拉力F在y方向的分量，故有

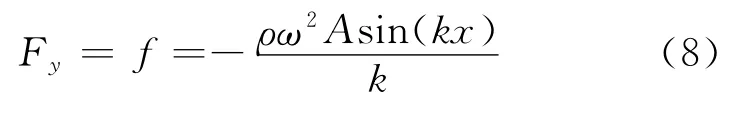
由图2可知F在x方向的分量Fx＝Fycotθ，其中θ满足

故有

其中，u＝ω／k为简谐波的波速.这说明要在细绳上传输弹性横波，细绳的两端必须被用力拉紧，且波速（速率）与绳内张力在波传播方向上分量的关系为

由式（8）和式（10）可得，M处的质元对右侧细绳拉力大小为

F来源于M点质元拉伸所产生的张力.在细绳的弹性范围内，根据胡克定律T＝k0δl以及弹性势能表达式Eps＝k0δl2／2，质元的弹性势能可以表示为

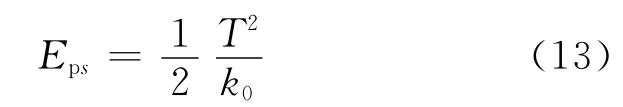
即质元的弹性势能正比于张力的平方，由式（12）可得

式（14）中右边第一项来源于细绳在x方向上的拉伸，不随时间和位置改变，为质元起振前已具有的势能；第二项来源于质元在平衡位置附近振动所产生的弹性形变.因此，简谐波的势能仅包含第二项.利用式（5）消去x，可得

与式（4）比较可以看到质元的动能与势能关于位移y具有类似的函数关系，仅系数的形式有所差别，下面证明两者的系数也是相等的.

原长为dx的质元，在简谐横波通过时被拉长为将式（5）代入可得质元长度的增量为

相应地，其张力大小由｜Fx｜增大到F.则根据胡克定律，该质元的劲度系数为

代入式（15）可得

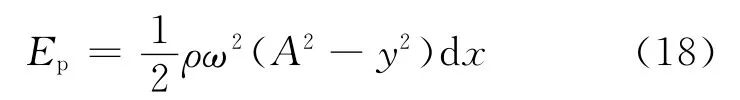
与式（4）给出的质元振动动能完全相同.相应地，细绳上同一位置的动能密度与势能密度亦相同.

3 纵波的情况

以上基于细绳上传播的简谐横波证明了同一质元具有等值的振动动能与弹性势能，对于纵波亦可作类似论证，简述如下.如用y表示质元偏离平衡位置的位移（此时位移沿x轴方向），各质元的动能及M，N段所受的合力仍可由式（4）和式（7）表示.因N点的质元无形变，故M点的质元张力大小为

对于纵波，原长为dx的质元形变量取决于质元两侧的位移之差，故有

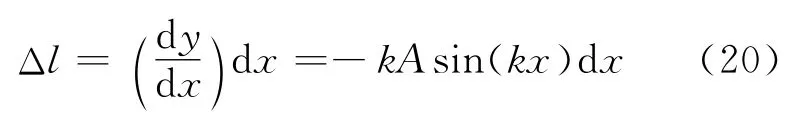
则质元的弹性势能为

与横波的表达式相同，故势能密度与动能密度相等的结论对简谐纵波同样适用.

[1]叶帆.关于连续介质中横波的能量探讨 [J].大学物理，2008，27（9）：19-21.

[2]张文杰，曹阳.大学物理教程 [M].北京：中国农业大学出版社，2009.

[3]汪新文，唐世清，许成科，等.平面简谐波势能的简易分析方法 [J].湖南科技学院学报，2012，33（8）：22-23.

[4]郭芳英，闫夷平，李爱玲.用横波推导简谐波的能量 [J].物理与工程，2003，12（2）：16-17.

[5]程守洙，江之永.普通物理学 第三册[M].5版.北京：高等教育出版社，1998.