关于“关于克劳修斯等式证明的再讨论”的讨论

蒋小勤

(海军工程大学应用物理系，湖北 武汉　430033)

教学经验交流

关于“关于克劳修斯等式证明的再讨论”的讨论

蒋小勤

(海军工程大学应用物理系，湖北 武汉430033)

摘要指出“关于克劳修斯等式证明的再讨论”一文论证过程中存在的问题，提出了一种在相邻卡诺循环之间过渡的循环路径，并证明了用若干个卡诺循环逼近任意可逆循环的可行性及其等价性。本文的研究支持主流热学教材中“用若干个完整的卡诺循环去分解任意循环，相邻的两个卡诺循环之间的重叠部分在两次循环中相互抵消”的论证方法。但现行教材的论述过程确实存在过于简略、不够严谨的问题，本文在阐明用卡诺循环分解任意循环的“等效性”内涵的基础上，采用泰勒级数展开及极限理论等高等数学方法，完善了克劳修斯等式的证明过程.

关键词克劳修斯等式；卡诺循环；任意可逆循环；可逆过程

REVIEW “ON THE PROOF OF CLAUSIUS EQUALITY (CONTINUED)”

Jiang Xiaoqin

(Department of Applied Physics, Naval University of Engineering, Wuhan, Hubei 430033)

AbstractSeveral problems occurred in the argumentation process of the paper “On the Proof of Clausius Equality (Continued)” have been pointed out. One kind of cycling path serving as a transition among neighboring Carnot cycles has been proposed. The feasibility and equivalence of approaching arbitrary cycle by several Carnot cycles has been proven. This article stands with the argumentation method for dividing arbitrary cycle by several complete Carnot cycles, where the overlapping part between neighboring Carnot cycles are neutralized due to the opposite loop directions, in main stream thermal physics textbooks. But it is a real fact that the proof procedure in textbooks is too sketchy and rather loosely in mathematics. Using Taylor’s series and limit theorem, a complete proof of Clausius equality with the necessary process have been presented in this paper.

Key wordsClausius equality; Carnot cycle; arbitrary reversible cycle; reversible process

熵是热力学系统的一个重要的态函数，熵的概念还被推广到了现代信息学等领域中，备受广大科技工作者的关注.工科大学物理课程将熵列入基本教学内容.现行的热学教材通常循着先介绍“卡诺循环”，再介绍“克劳修斯等式不等式”的路径，自然地引入熵这个态函数.然而由于在推导“克劳修斯等式不等式”这个环节，为了重点突出其物理意义，大多教材采用文字论述，没有给出严格的数学证明过程.这就引发了物理教学工作者对这个问题的广泛讨论[1-3]. 最近《物理与工程》杂志上刊出的 “关于克劳修斯等式证明的再讨论”一文[3](以下简称为“再讨论”)认为一些主流热学教材中证明克劳修斯等式的做法，即“用若干个完整的卡诺循环去分解任意循环，认为相邻的两个卡诺循环之间的重叠部分在两次循环中相互抵消”的论证方法存在问题，并利用简化的分解图证明主流热学教材中有关论证的问题在于“工作物质无法在两个相邻的卡诺循环之间过渡”，进一步指出“卡诺循环之间的重叠部分根本未曾被经历，并无‘抵消’之说”. 又一次将克劳修斯等式的证明问题提了出来.本文研讨的问题是：

(1) 果然像“再讨论”一文的论述那样，主流的热学教材都犯了同样的错误吗？

(2) 如果热学教材中有关论述定性上并没有错，只是论证不够严谨的话，能否完善其论证过程，并避免冗长的数学推导，保留清晰直观的物理图像，以便于在大学物理课程教学中运用?

对问题(1)，本文提出了一种在相邻卡诺循环之间过渡的循环路径，并证明了用若干个微小卡诺循环逼近任意循环的可行性及其等价性.对问题(2)，本文提出了选取微小卡诺循环等温线应满足的“等效性”条件，补充了必要的热温比积分计算过程，完善了克劳修斯等式的证明.

1任意可逆循环的卡诺循环分解

为了证明克劳修斯等式，即对于任意的可逆循环过程有

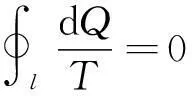
(1-1)

大学物理教材中常借用卡诺循环的性质：

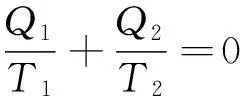
(1-2)

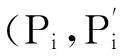
“……任意两个相邻的微小可逆卡诺循环总有一段绝热线是共有的，但进行的方向相反从而效果完全抵消，因此，这一连串微小的可逆卡诺循环的总效果就是图中锯齿形包络线所表示的循环过程……”.从直观看“如果使每个微小卡诺循环无限小，从而使卡诺循环的数目n→∞,则这锯齿形路径所表示的循环过程就将无限趋近于原来考虑的任意可逆循环过程”，进而利用卡诺循环的性质式(1-2)，直接得到克劳修斯等式(1-1)[4,5].对此有文献[1,2 ]提出疑问，认为这样的论证不够严谨.这些文献大都是从如何完善证明过程的角度展开分析与讨论的.最近《物理与工程》上刊出的“再讨论”一文则提出了“工作物质无法在两个相邻的卡诺循环之间过渡”“卡诺循环之间的重叠部分根本未曾被经历，并无‘抵消’之说”的论断，从更为基本的角度对主流教材中有关克劳修斯等式的证明方法提出质疑[3].“再讨论”一文认为：“……这样的陈述表明每个微小的循环都要完整地进行(否则不能说它们相邻的部分抵消)，但这样立即会使过程陷入死循环……”, 进而用简图(“再讨论”一文之图2)说明在完成第一个卡诺循环后系统回到了起点,“……没有办法过渡到第二个循环从而走完全部锯齿形包络线”.“再讨论”一文断言“要让系统无重复地经历所有锯齿形包络线，图中的bg段必须不能被经历，……并无‘抵消’之说，……,中间所谓重复部分，均没有实际经历过”.本文认为“再讨论”一文的这些观点值得商榷.

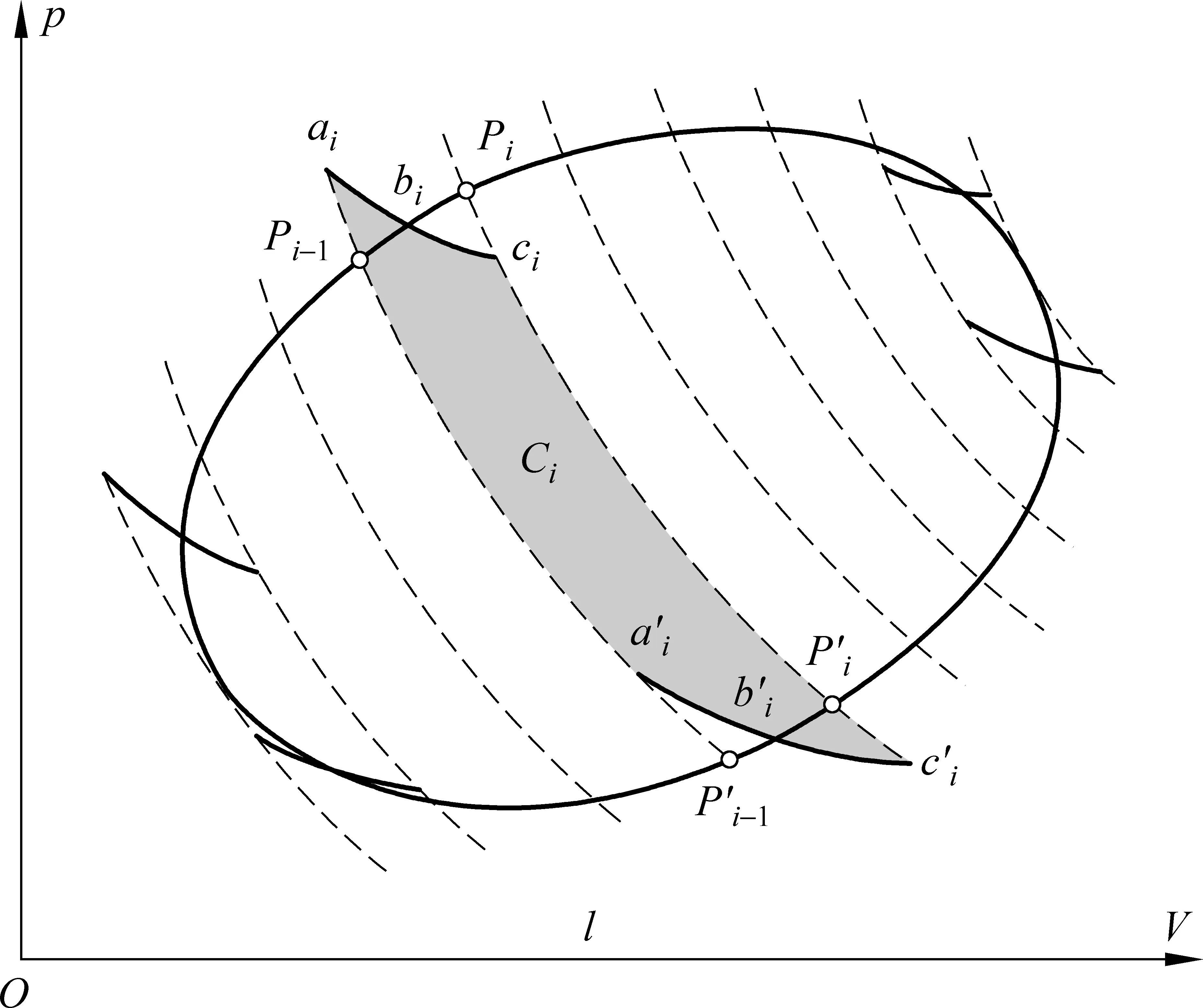
图1　任意可逆循环l的卡诺循环分解示意图图中阴影区域代表第i个卡诺循环Ci

2卡诺循环分解的等效性

本文认为教材中将任意可逆循环l分解为n个微小的卡诺循环是一种等效论证方法.这里要明确“等效”这个概念的含义，重要的是原任意循环l与n个微小的卡诺循环的总效果，而非系统经历循环路径的细节，尤其对于可逆过程而言，正、逆两次过程的效果为零.“再讨论”一文之所以会得到“……没有办法过渡到第二个循环从而走完全部锯齿形包络线”的断言，就源于“要让系统无重复地经历所有锯齿形包络线,……”这个细节之上.其实如果某一段锯齿形包络线被多走了一个来回，其总的效果是互相抵消的.所以只要不拘泥于系统经历路径的细节，而注重总的效果的话，就可以设计由n个卡诺循环构成的循环过程来逼近一个任意可逆循环过程.本文用一个只包含4个卡诺循环的简图说明之(如图2所示)，当系统从P0点出发沿着第一个卡诺循环路径C1回到起点P0后，继续沿锯齿路径P0a1b1c1P1到达P1点，再沿着C2完成第二个卡诺循环……, 如此继续，直到完成全部卡诺循环后系统到达Pn-1(图2中的P3),再令系统从Pn-1沿锯齿路径逆向回到P0，此时系统经历过程的总效果与n个独立的卡诺循环等效.进一步，由于相邻的两个卡诺循环之间的重叠部分在两次循环中相互抵消，则系统经历过程的总效果也与以这n个独立的卡诺循环的外缘构成的锯齿路径循环等效. 由此可见：“再讨论”一文所谓的“陷入死循环”“……并无‘抵消’之说”“……中间所谓重复部分，均没有实际经历过”，以及“……这样容易使初学者产生误解，……”等论断都不能成立.

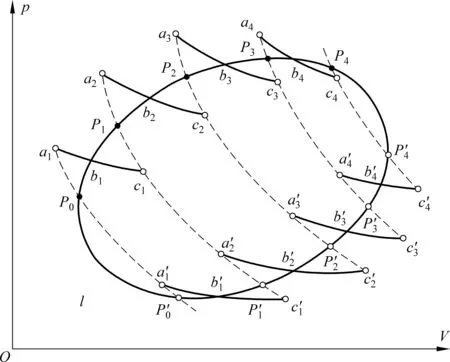
图2　用4个卡诺循环分解任意可逆循环l的简图图中是等温线与循环l的交点.

3克劳修斯等式的严格证明

由于教学对象不同，教材中有关克劳修斯等式不等式的证明方法也各不相同，例如文献[6,7]采用费米法，文献[8]则以理想气体为例，从微观状态数玻尔兹曼熵公式及热力学第一定律推得

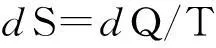
(3-1)

再由熵是状态函数，推得任意可逆循环过程的克劳修斯等式(1-1).

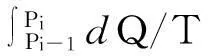
有关第一个步骤，对教材[8]中的表述：“当小卡诺循环的数目趋向无穷大时，锯齿形曲线就趋向原可逆循环……”,以及教材[9,10]中类似的表述，文献[2]提出了异议，其主要观点是，锯齿形曲线的斜率与原循环回路l的不等、其长度也不同.本文作者认为这里的分歧来自于对“趋向”一词内涵的理解上.如果把“趋向”理解为“全同”，就会出现文献[2]指出的问题.但是，显然这里的“趋向”一词不能作“全同”来理解，而应当理解为数学上的“收敛”，物理上理解为循环效果的“等效”.

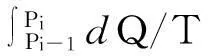
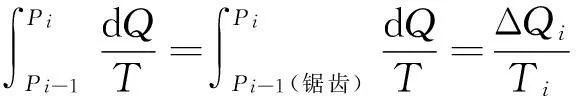
(3-2)

其中，Ti是小卡诺循环高温等温线的温度，ΔQi是系统工质与热源Ti交换的热量.同理得

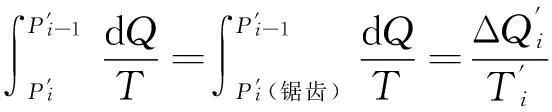
(3-3)

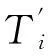
将沿任意可逆循环路径l热温比的积分式写成分段积分形式

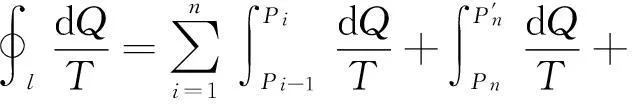
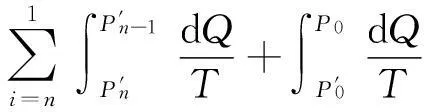
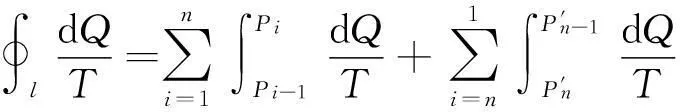
(3-4)

将式(3-1)、式(3-2)代入式(3-4)得

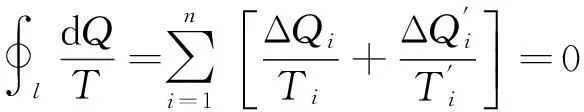
(3-5)

这就证明了克劳修斯等式.这里运用了卡诺循环的性质式(1-2)，即

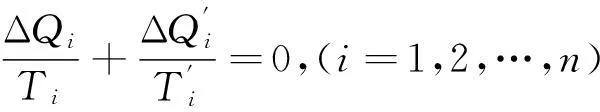
(3-6)

如果不采用“等面积法”选取微小卡诺循环的等温线，将热力学第一定律ΔQ=ΔU+A运用于由l上微元(Pi-1,Pi)与锯齿路径(Pi-1aibiciPi)围成的闭合循环(ΔU=0),则有

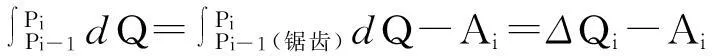
(3-7)

其中，Ai=SΔPi-1aibi-SΔbiciPi是在循环过程(Pi-1aibiciPibiPi-1)中系统对外输出的净功，由于与ΔQi相比Ai是高阶无穷小量[11]，所以有

(3-8)

对系统在微元(Pi-1,Pi)范围内的温度T(p,V)，在等温线与l的交点bi(pi,Vi)处作泰勒级数展开，取线性近似为

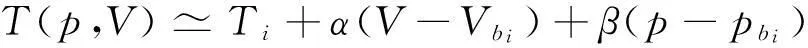
(3-9)

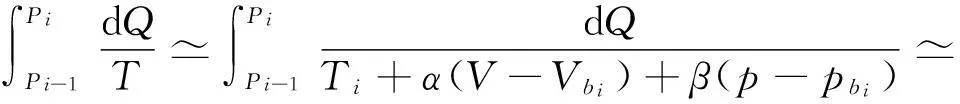
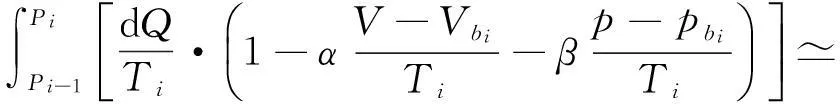
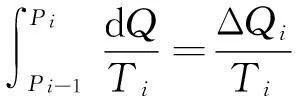
(3-10)

可见，只要微小卡诺循环的等温线与原任意循环l在(Pi-1,Pi)微元上相交于bi,即使曲边三角形ΔPi-1aibi与ΔbiciPi的面积不相等，式(3-2)与式(3-3)在n→∞的极限意义下仍然严格成立.“等面积法” 是众多可能的等温线取法中的一种，并不是必须的.但由于等面积法的物理概念直观明了，数学推导过程形式简单，因而被广为采用.

4结语

综合以上分析可见：

(1) 主流热学教材中“用若干个完整的卡诺循环去分解任意可逆循环，相邻的两个卡诺循环之间的重叠部分在两次循环中相互抵消”的论证方法原则上是可行的，并不存在“再讨论”一文列举的问题.

(2) 现行热学教材中有关克劳修斯等式的证明确实存在文字论证过于简单、不够严谨的问题.有些用语，例如“当小卡诺循环的数目趋向无穷大时，锯齿形曲线就趋向原可逆循环……”表述上存在歧义.产生歧义的主要原因来自于对卡诺循环分解与原循环“等效性”的理解上.这里“锯齿形曲线就趋向原可逆循环”应当理解为：当n→∞时，由n个卡诺循环外缘绝热线与等温线构成的锯齿循环曲线上的所有点收敛到l之上；锯齿循环曲线所围面积收敛于原循环l所围的面积.

(3) 对于克劳修斯等式证明问题，如果将“等效性”理解为原循环l上被微小卡诺循绝热线分割的微元(Pi-1,Pi)上热温比的积分值，与沿相应的锯齿形路径(Pi-1aibiciPi)热温比的积分值，在n→∞时的极限意义下相等，则借助于卡诺循环分解方法，克劳修斯等式可以从数学上加以严格证明.

参考文献

[1]张锡钧.任意可逆循环如何分解为一系列卡诺循环[J].山东师大学报(自然科学版),1990,5(4):105-107.

[2]贺成绪,张可,谈应潮,等.在可逆循环热温比之和为零的推导中存在的问题及解决办法[J].物理与工程, 2005, 15(2):15-17.

[3]李品钧.关于克劳修斯等式证明的再讨论[J].物理与工程, 2014,24(5):64-65.

[4]李椿,章立源,钱尚武.热学[M].北京:高等教育出版社, 2008:169.

[5]秦允豪.热学[M].北京:高等教育出版社,2011:271-272.

[6]赵凯华,罗蔚茵.热学[M].北京:高等教育出版社,1998: 190-192.

[7]马春曦,朱元海,桑希勤.克劳修斯不等式证明的一点补充[J].大庆石油学院学报,2006,30(5):93-95.

[8]张三慧.大学物理学：第二册,热学[M].北京:清华大学出版社,1999:187-195.

[9]陈守洙,江之永.普通物理学[M].北京:高等教育出版社, 1998:376-377.

[10]马文蔚,物理学[M].北京:高等教育出版社,2000:211-213

[11]李椿,章立源,钱尚武.热学[M].北京:人民教育出版社，1978:257.

■

作者简介:蒋小勤, 男, 教授，主要从事物理教学科研工作，研究方向为流体物理学. xqjiang888@qq.com

收稿日期:2015-01-05