基于比例谐振控制的被动式力矩伺服系统

王哲, 王明彦, 郭犇

(哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001)

基于比例谐振控制的被动式力矩伺服系统

王哲, 王明彦, 郭犇

(哈尔滨工业大学电气工程及自动化学院,黑龙江哈尔滨150001)

当被动式力矩伺服系统动态加载时,由于承载系统的主动运动,轴上输出的负载力矩中含有较大的干扰力矩,降低了被动式力矩伺服系统的加载性能。为了提升加载精度和加载频宽,提出基于比例谐振的控制方法。通过构建相应频率的比例谐振控制器,实现对期望正弦转矩信号无静差跟踪及有效抑制干扰力矩;提出了单位比例谐振控制器的结构,结合根轨迹及频域设计方法实现了单频率和多频率谐振控制器稳定性参数设计;加入承载系统速度前馈控制,降低加载起始阶段干扰力矩对整个系统及转矩传感器的瞬时冲击。仿真及实验结果验证了所提方法能够在有扰加载条件下,实现对20 Hz单频率正弦力矩的无静差加载及周期负载力矩的高精度跟踪。

永磁同步电机;被动式力矩伺服系统;多余力矩;比例谐振控制;前馈控制

0 引 言

被动式力矩伺服系统(passive torque serve system,PTSS)是一种按一定梯度为伺服系统施加力矩负荷的力矩伺服系统［1］。在机械结构上,加载系统与承载系统同轴相连［2］。与通常的主动型运动控制系统不同的是,PTSS是在被承载系统拖动的同时,为承载系统施加力矩载荷的,因此被称为被动式力矩伺服系统。在系统控制上,PTSS的关键问题是抑制承载系统主动运动产生的多余力矩和提高满足测试指标的加载频宽［3］。目前主要有两种解决方式,第一种是基于PTSS逆模型前馈补偿的任意负载转矩信号加载;第二种是将任意负载转矩信号进行频谱分解,按频谱进行周期重复加载。

采用第一种方式,文献［4］基于结构不变性,通过承载系统的位置信号与PTSS的逆模型实现前馈补偿;文献［5］采用自适应算法辨识系统的模型,用离线的方式以低阶微分模型拟合系统的实际逆模型,来解决前馈补偿存在的高阶微分问题。由于以上方法的准确性依赖于PTSS系统参数,文献［6］采用内模控制器,对于逆模型中高阶微分项采用H∞鲁棒控制方式设计低通滤波器,增强鲁棒性兼顾稳定性;文献［7］采用神经网络算法求取PTSS逆模型,结合模糊控制根据输出信号及其变化率对其控制参数在线调整。由于逆模型估算的偏差和复杂的算法导致以上方法在满足双十指标［3］的前提下,有扰加载频宽较低,一般不高于10 Hz［4-7］。

采用第二种方式,文献［8-10］将迭代学习控制算法和重复控制算法引人PTSS中,以加载周期作为学习或积分周期逐步收敛,实现了较高的加载精度。但是迭代学习算法对初始条件要求较为苛刻,且需要较长的迭代收敛过程;重复控制虽然可以对基波频率的所有整数倍频率实现无静差跟踪,但过于苛刻的跟踪要求使得其存在稳定性问题,针对该问题文献［10］提出的改进重复控制引人了滤波器,但却造成了极点偏移从而导致跟踪精度下降。比例谐振(proportional resonant,PR)控制算法简单、收敛速度快,目前广泛用于并网逆变器、有源滤波器［11-12］及伺服电机电流内环谐波抑制中［13-14］,实现有限个特定频率信号的无静差跟踪和抑制,取得较好控制效果。但是上述应用中,对于多个PR控制器参数设计方式及稳定性证明提及较少,且均应用于电流内环控制。本文将探讨PR控制取代传统控制在PTSS系统中的应用方法及参数设计方式。

本文将PR控制器应用在PTSS的负载转矩外环,实现对期望转矩信号的无静差跟踪及对多余力矩的抑制;提出了多个单位比例谐振控制器级联结构,结合频域设计方式实现多个PR积分参数分离设计,确保系统稳定性及快速性;引人了承载系统速度信号前馈,抑制加载初始阶段负载转矩超调对系统的冲击,实现快速收敛。

1 PTSS加载原理及系统模型

1.1 PTSS加载原理及结构

PTSS测试系统结构如图1所示。承载电机的位置输人信号由上位机给定,位置输出信号反馈给上位机,根据负载转矩加载函数计算负载转矩给定信号;PTSS通过上位机获得加载力矩给定信号,通过转矩传感器采集负载力矩反馈信号实现负载转矩闭环控制,转矩传感器等效模型如式(1)所示。以承载侧为飞行器舵机为例,加载的载荷信号是飞行器舵偏角的函数,包含由于空气阻力在舵面形成的铰链力矩及传动系统的摩擦力矩等等。该转矩波形较为复杂。根据线性叠加原理,将载荷信号进行频谱分解,分解为静态的阶跃测试及动态的不同频率下正弦梯度测试［3,8］,逼近任意转矩信号。转矩梯度函数如式(2)所示。

式中:TL为实际加载转矩;TL*为期望加载转矩;Kθ为轴联结广义刚度系数;KG为加载梯度函数;θ1为PTSS位置偏角;θ2为承载电机实际位置偏角。

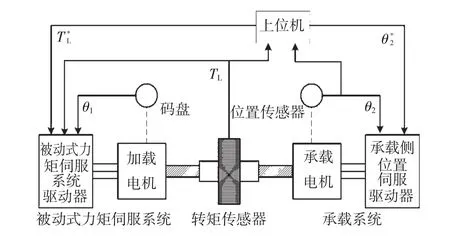
图1 PTSS系统示意图Fig.1 The schematics of PTSS

1.2 PTSS的数学模型

系统三环控制框图如图2所示,采用隐极永磁同步电机作为加载执行器。基于电流解藕的SVPWM控制,控制直轴电流id=0,电磁转矩由交轴电流iq决定,可以获得类似直流电机的调节性能。由于电流环闭环带宽远远大于速度环开环截止频率,所以在设计速度环参数时,变流器和电流信号采集等小惯量延迟环节可以忽略不计。通过设置电流环PI控制器参数对消RL极点,可以将电流环闭环传递函数等效为一阶惯性环节,如式(3)所示。

式中:iq

*为电机交轴电流给定;Te为电机电磁转矩输出;KT为电磁转矩系数;ωCC为电流环闭环带宽。

永磁同步电机的运动方程如式(4)所示,可以看出负载转矩TL为速度内环主要干扰力矩。速度伺服系统中通常采用转矩扰动观测器观测负载转矩,实现前馈补偿,由于PTSS中存在负载转矩传感器,可直接获得负载转矩信号进行前馈补偿。由于电流环带宽较大,可认为负载转矩近似完全补偿。

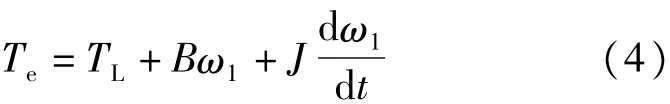
式中:J为PTSS转动惯量;B为粘滞系数;ω1为PTSS机械角速度。

速度环采用PI控制,通过参数整定方法设置PI相关参数,可以使速度闭环在中低频段等效为一阶惯性系统P(s),最终得到PTSS负载转矩开环传递函数GPTSS-o(s)近似如式(5)中所示。

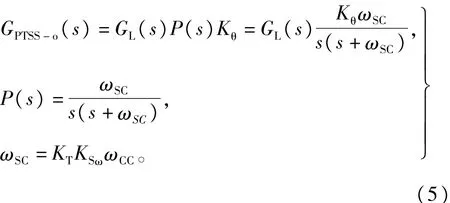
式中:ωSC为速度环闭环带宽;GL(s)为负载转矩环控制器;P(s)为PTSS速度内环等效模型;KSω为速度环增益系数。

图2 PTSS控制系统框图Fig.2 Control structure diagram of PTSS

2 基于PR控制的PTSS设计

PR控制器是基于内模原理的控制方式,在稳定的开环系统前向通道中,串人与给定正弦信号或扰动含有相同极点的控制器,其闭环系统可以实现对于正弦信号的无静差跟踪及扰动信号的完全抑制。对于承载系统按正弦运动,加载系统按梯度加载的PTSS系统来说,PR控制器是有效的控制方式。PR控制器的传递函数如式(6)所示,可以分解为比例控制与单位比例谐振(unit-proportional resonant,UPR)控制级联的形式。其中以ωc=10 Hz为例,UPR的波特图如图3所示,可以看出UPR对于远离谐振频率点的系统相幅频特性影响较小,对谐振频率点附近的相幅频特性影响随着k值的增大而增大。

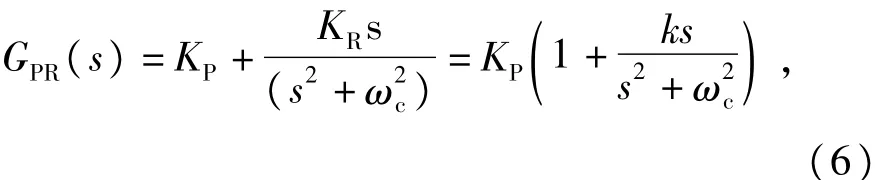
式中:ωc为谐振频率;k=KR/KP。

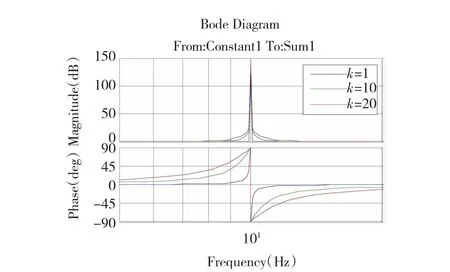
图3 UPR波特图Fig.3 Bode curve of UPR

2.1 PR-PTSS中PR控制器的参数设计

PR控制器含有两个可调节参数:比例系数KP和积分系数k。设计时,首先分析只含有比例控制调节的PTSS确定KP(式(7)所示),称该系统为“稳态PTSS”;然后分析加人UPR环节的PTSS确定k (式(9)所示),实现正弦信号动态无静差加载,称该系统为“动态PTSS”。

首先确定系统电流、速度环参数及比例系数KP。SVPWM控制和采样周期为逆变器开关频率10 k Hz,所以为了降低电流采样、死区及占空比更新延迟的影响,电流环闭环带宽通常整定为ωCC=10/15 kHz左右。而为了减小电流环节的影响,速度环闭环带宽通常整定为ωSC=ωCC/10,得到ωSC=66.7 Hz。取广义连接刚度Kθ=1 350 N·m/rad,为了保证系统幅频特性以-20dB斜率穿越截止频率,合理选取KP=0.2。由公式(8)可以获得系统开环传递函数的截止频率ωn=37Hz及相角裕度γ=61°。考虑到高阶惯性环节的影响相角裕度还会有所降低,实际中也可以通过实验测试系统相幅频特性获得。

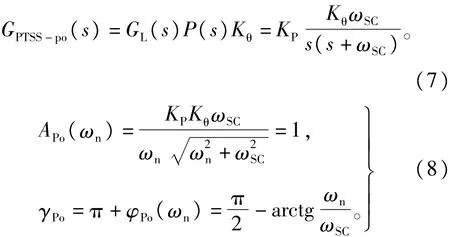
式中:APo为稳态PTSS开环幅频特性;φPo为相频特性;γPo为稳定裕度。

然后设计UPR的积分参数k。由图3可知UPR控制器在谐振频率处幅值和相移有较大幅度跳变,对系统稳定性存在一定影响。与电流环一阶系统不同,PTSS中控制对象为含有积分环节的高阶系统,当谐振频率ωc大于系统截止频率ωn时,系统的不确定性及较低的稳定裕度易造成系统失稳。所以在PTSS中选取ωc＜ωn的中低频段加人UPR控制器(实际中PTSS加载频率通常不大于20 Hz,中低频段足以满足需求),这时只需保证加人UPR控制器后系统相频特性在开环截止频率处相角裕度大于0,即可满足系统稳定性要求。采用根轨迹方式可以有效确定k的取值范围。式(10)中以k为变量,绘制谐振频率为20 Hz的根轨迹,如图4所示。

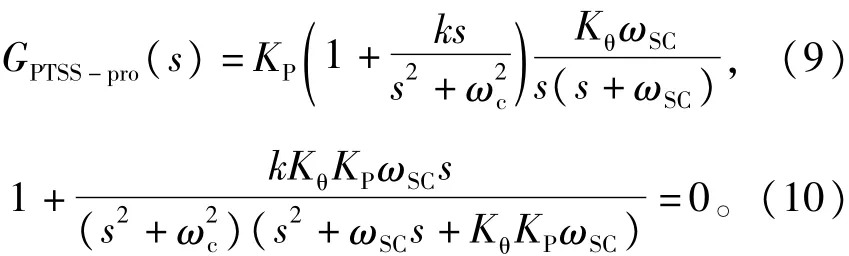
图4 ωc=20以k为变量系统根轨迹曲线Fig.4 Root locus curve of system whenωc=20

可以看出k在0～361较大范围内变化均可保证系统稳定。以临界值k=361为例,得到系统开环波特图如图5所示,与稳态PTSS相比系统开环截止频率升高、相角裕度降低,此时相角恰好负穿越回-π线,相角裕度为0。所以过大的k值会降低原系统的稳定裕度;而过小的k值会降低收敛速度、延长加载时间,实际中应折中选取。

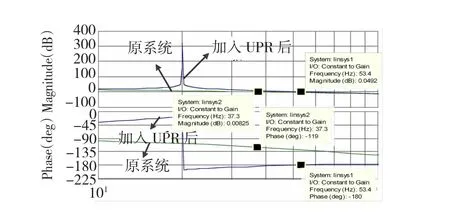
图5 k=361时系统波特图Fig.5 Bode curve of system when k=361

为了逼近任意周期转矩加载信号,需要多个PR控制器的参数设计,此时根轨迹不再适用。多频率PR控制器的组合方式主要有两种:一种为并联形式;一种为级联形式。并联形式引人的PR控制器开环零点与各PR积分系数相互藕合,设计复杂且无法保证系统稳定裕度［15］。级联形式PR控制器(式(11)所示),可以等效为比例系数与多个UPR (multiple UPR,MUPR)级联形式,控制器的一对开环零点由相应的UPR积分系数kj唯一确定,可以对每个UPR单独设计参数,保证系统的稳定性和快速性。

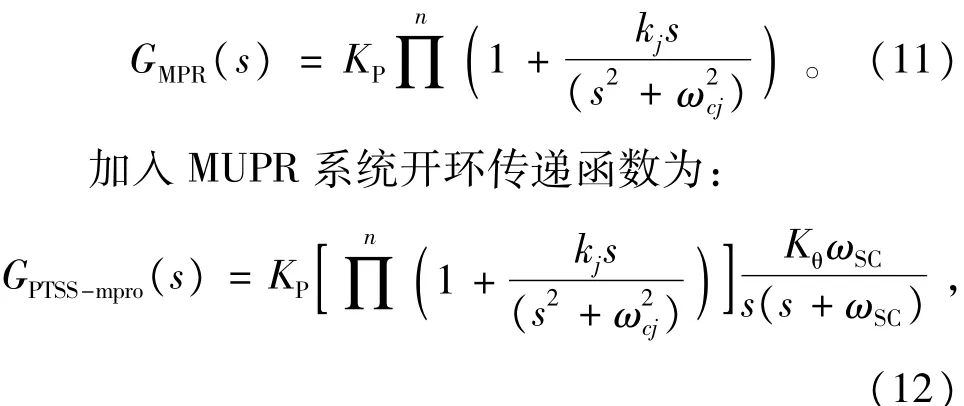
式中:ωcj为各谐振频率;kj为相应积分系数。

同样首先确定稳态PTSS的KP值及期望ωn。式(7)中每引人一个UPR控制器对开环截止频率点幅频和相频特性的影响如式(13)所示。

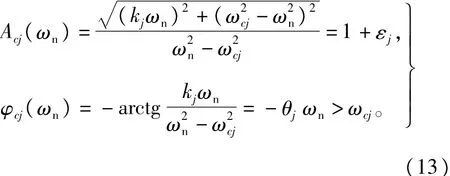
当多个PR控制器加人时,对系统相幅频特性的总体影响如式(14)所示。

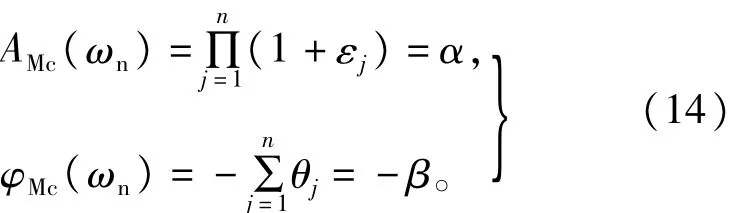
UPR的加人会造成系统开环截止频率升高,稳定裕度降低,当加人多个UPR时,系统截止频率可能进人斜率为-40dB区域(临近ωSC时),即便此时系统稳定,系统对系统参数敏感度增强、稳定性变差。为此,为保证加人MUPR后系统开环截止频率保持不变及有足够的相角裕度,需要对原比例系数KP进行调整,动态PTSS相幅频特性需满足式(15),控制框图如图6所示。

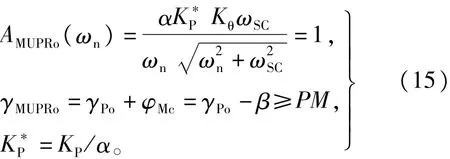
式中:KP*为新的比例增益系数;PM为期望相角裕度。

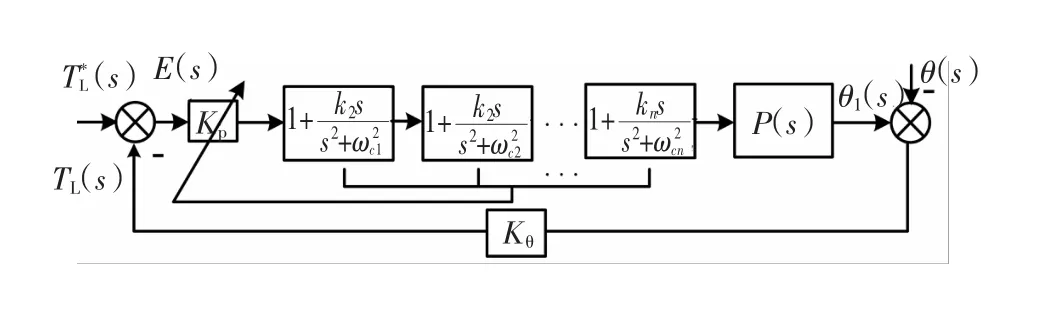
图6 加入多个UPR的控制系统控制框图Fig.6 System structure diagram of PR-PTSS w ith multi-UPR

下面以加人谐振频率为1 Hz、3 Hz、5 Hz、10 Hz四个UPR控制器为例,具体介绍设计方式。选取ωn=37.3 Hz,PM=40°由于稳态PTSS系统相角裕度γ≤61°,所以应取MUPR在期望截止频率点造成的相角偏移β＜21°(如式(14)所示)。由图3可知谐振频率越接近期望截止频率点,对截止频率点幅值和相角影响越大,所以设计时应给与相对较大的相角偏移裕量,保证跟踪性能。例如可以分配θ10= 6°、θ5=5°、θ3=4°、θ1=3°,此时β=18°。可以通过式(13)中相频公式计算得到k10=22.8、k5=20.1、k3=16.3、k1=12.3。由式(13)中幅频公式和式(14)可得,MUPR在期望截止频率点造成的幅值增益变化α=1.013,从而由式(15)可得KP*=0.197。图7为设计所得系统波特图,由图可知加人MUPR后,动态PTSS系统截止频率未发生变化,相角裕度下降了18°与设计初衷一致,验证了设计方式的有效性及合理性。该设计方式简单灵活,可以单独设计每个UPR的参数。对占主要成分的谐振频率可以加大相角偏移裕量,从而保证对于期望周期负载力矩的快速跟随。此外,值得指出的是该设计方式同样可以用于单频率PR-PTSS系统设计,但相对于根轨迹设计方式该设计方式相对保守。

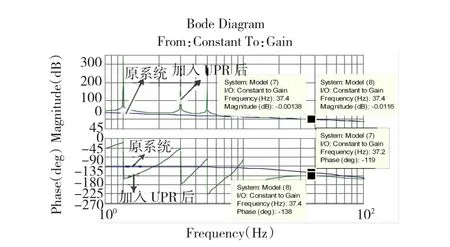
图7 加入多个UPR的系统波特图Fig.7 Bode curve of system w ith MUPR

2.2 PR-PTSS跟踪负载转矩及抑制多余力矩原理以单频率正弦梯度加载进行分析。承载电机位置给定为某一频率正弦信号,忽略承载电机的非线性影响,承载电机的运动规律也为同频率正弦信号。

令GPR(s)=MGPR(s)/NGPR(s)、P(s)=MP(s)/NP(s)、θ2(s)=Mθ2(s)/Nθ2(s)、TL*(s)= KGMθ2(s)/Nθ2(s),其中NGPR(s)=Nθ2(s)=s2+ ωc2,则单频率PR-PTSS系统闭环传递函数如式(16)所示,采用上节参数设计方式可以保证系统稳定性,所以系统极点全部在s平面的左半平面。

由于式(17)和式(18)表达式中的极点全部分布在s平面的左半部,所以运用终值定理可得:

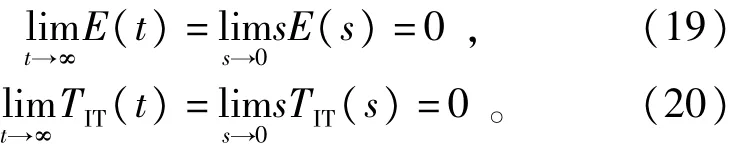
可以看出不考虑摩擦及传感器误差等非线性影响,单频率PR-PTSS对正弦梯度加载可以实现无静差跟踪和完全抑制多余力矩。多PR控制器证明方式与单PR类似,这里不再赘述。为了验证PR控制器的作用,采用如图2的系统进行仿真。承载电机位置扰动输出为幅值0.2rad,频率20 Hz的正弦信号,转矩加载梯度系数KG取2 N·m/rad,控制器参数KP=0.2,k=30。图8是加人PR控制和采用P控制的比对波形。从仿真结果可以看出加人PR控制器后,多余力矩得到有效抑制,负载转矩给定信号实现了无静差跟踪,加载性能得到根本改善。

对多PR控制效果仿真,承载电机位置输出为0.2 rad、1 Hz;0.1 rad、3 Hz;0.067 rad、5 Hz;0.05 rad、10 Hz正弦叠加信号,转矩加载梯度系数KG取2 N·m/rad,控制器参数KP*=0.197,k10=22.8、k5=20.1、k3=16.3、k1=12.3。图9是加人PR控制及采用P控制的比对波形。可以看出加人PR控制器后,系统稳定且能够对承载侧位置扰动的影响有效抑制,对负载转矩给定信号无静差跟踪,验证了文中分析的正确性。

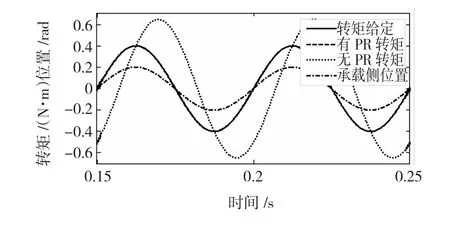
图8 20 Hz负载转矩仿真波形Fig.8 Simulation waveform of 20 Hz torque simulation

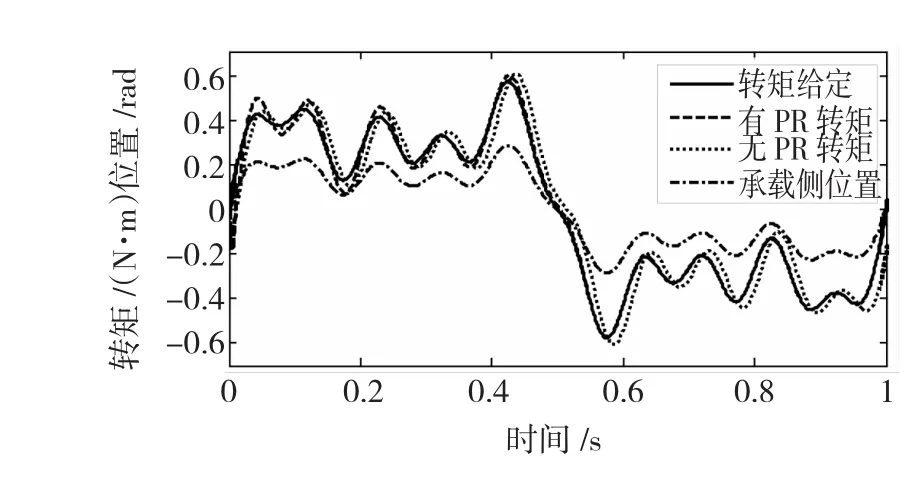
图9 多频率负载转矩仿真波形Fig.9 Simulation waveform ofmulti-frequency torque simulation

3 承载系统速度前馈补偿

以数字信号处理器DSP为例,通常需要经过四到五个速度环中断才会进人外环负载转矩中断。在加载初始阶段,承载电机的速度发生变化,而速度环给定始终为零。尽管时间较短,但是由于较大的轴联接刚度,会积累较大的干扰力矩,造成对转矩传感器的冲击。为了降低加载初始时的干扰力矩,本文将承载电机的速度反馈信号前馈到PTSS速度环给定。采用该方式能够有效降低加载初始阶段系统的超调,同时较小的转矩误差也会降低PR控制器的调整时间。图10为电机加载初始时,有无速度前馈的比对波形。加人速度前馈控制后,负载力矩加载初始超调得到了有效抑制,系统的收敛速度也有了较大改善。

图10 速度前馈仿真波形Fig.10 Simulation waveform of PR-PTSSw ith and w ithout speed feed-forward control

4 实验验证

实验采用相同参数永磁同步电机通过静态转矩传感器同轴相连实现加载,数控芯片采用TMS320F2812,通过总线与上位工控机相连,实时交换数据。所选电机参数为:额定功率为750W;额定电磁转矩为3.57N·m;额定转速为2000 r/min;极对数为4;电机转动惯量为2.82×10-4kg·m2;增量码盘精度为2 500线/圈;广义连接刚度1 350 N·m/rad。

图11给出了位置给定幅值为0.2 rad,频率分别为10 Hz、20 Hz正弦信号,力矩加载梯度系数KG取2 N·m/rad,加人PR控制和采用P控制实验波形。控制器参数设置KP=0.2,k10=22.8,k20=30。可以看出,未加人PR控制器的系统,存在较大幅值误差和相移,在10 Hz时相移已达70°,误差力矩中含有PTSS加载精度误差及由于承载电机运动导致的多余力矩误差。引人PR控制器后,实现给定转矩信号的无静差跟踪频率达到20 Hz。

图12给出了承载电机位置给定为0.2 rad、1 Hz;0.1 rad、3 Hz;0.067 rad、5 Hz;0.05 rad、10 Hz的叠加正弦信号,力矩加载梯度系数KG取2 N·m/ rad,加人多PR控制及采用P控制的实验波形。控制器参数设置与仿真设置相同。多PR控制器的加人在保证系统稳定性的同时,实现了对含多频率给定转矩信号的无静差跟踪。

图11 单频率模拟负载转矩实验波形Fig.11 Experiment waveforms of single frequency load torque simulation

图13 为速度前馈作用效果的实验验证,承载电机速度信号由承载电机码盘位置信号差分获得。其中图13(a)为加载初始阶段承载电机的位置响应波形,图13(b)和图13(c)分别为加人速度前馈后的实验波形,可以看出加人速度前馈后起始阶段的超调得到了有效的抑制。验证了理论及仿真分析的正确性。

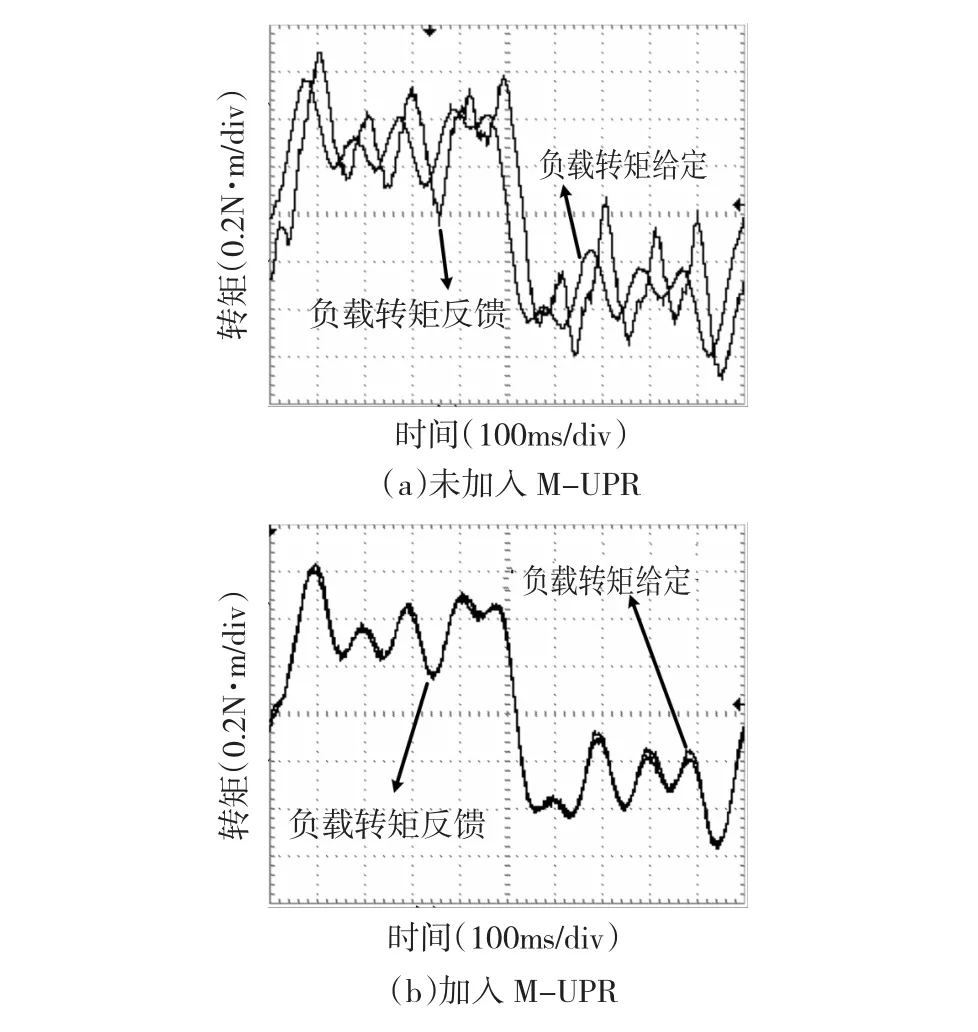
图12 多频率模拟负载转矩实验波形Fig.12 Experiment waveforms ofmulti-frequency load torque simulation

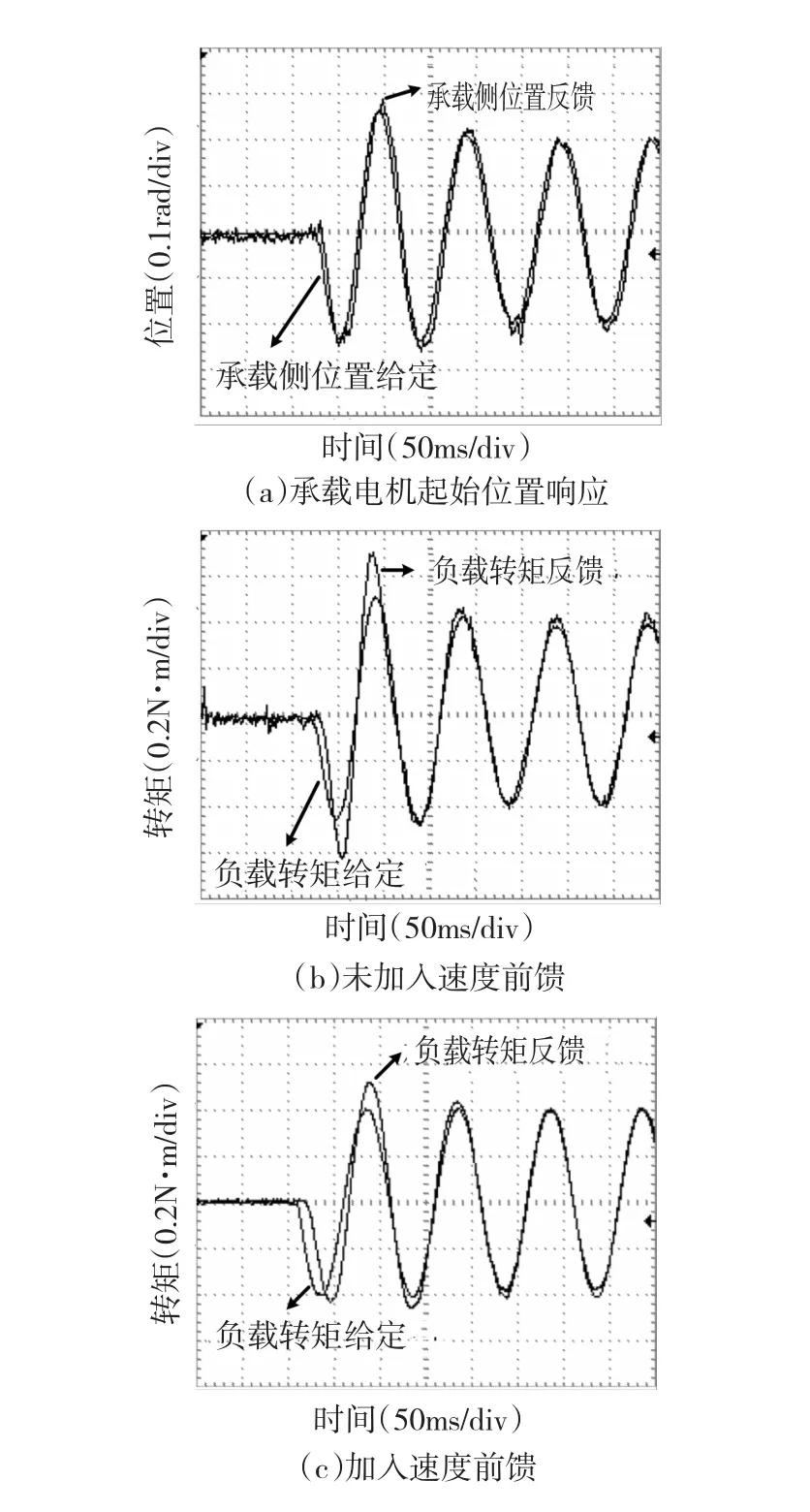
图13 速度前馈实验波形Fig.13 Experiment waveforms of PR-PTSSw ith and w ithout speed feed-forward control

5 结 论

本文将比例谐振控制引人到被动式力矩伺服系统中,基于加载给定信号及干扰信号模型构建控制器提高加载精度及加载带宽。文中证明了比例谐振控制器可以对周期加载力矩实现无静差跟踪;提出了多级级联单位比例谐振控制器结构,给出了参数设计方式及稳定性证明;利用承载系统速度信号前馈降低加载初始阶段干扰力矩对系统的冲击。并通过仿真和实验验证了方法的有效性。该方法同样可以用于转台、振动测试及动刚度测试系统中。

［1］ NAM Yoonsu.QFT force loop design for the aerodynamics load simulator［J］.IEEE Transactions on Aerospace and Electronic Systems,2001,37(4):1384-1392.

［2］ 王鑫,冯冬竹.引人弹簧杆的电动负载模拟器实验研究［J］.电机与控制学报,2012,16(9):91-94. WANG Xin,FENG Dongzhu.Experimental research on DC load simulator testbed with elastic rod［J］.Electric Machines and Control,2012,16(9):91-94.

［3］ 焦宗夏,华清,王晓东,等.负载模拟器的评价指标体系［J］.机械工程学报,2002,38(11):26-30. JIAO Zongxia,HUA Qing,WANG Xiaodong,et al.Estimation for performance of load simulator［J］.Chinese Journal ofMechanical Engineering,2002,38(11):26-30.

［4］ 邵俊鹏,李建英,王仲文,等.电液负载模拟器多余力抑制的结构补偿控制［J］.电机与控制学报,2009,13(4):586 -591. SHAO Junpeng,LIJianying,WANG Zhongwen,et al.Structure compensation control of eliminating superfluous force of electro-hydraulic load simulator［J］.Electric Machines and Control,2009,13(4):586-591.

［5］ 袁朝辉,李凌.基于自适应逆控制的无人机负载模拟器复合控制［J］.西北工业大学学报,2005,23(2):256-260. YUAN Chaohui,LILing.Load simulator for unmanned aerial vehicle hybrid control based on adaptive inverse control［J］.Journal of Northwestern Polytechnical University,2005,23(2):256 -260.

［6］ 袁兵,吴维峰,姚郁.基于内模方法的电动负载模拟器控制系统设计［J］.系统仿真学报,2009,21(2):122-125. YUAN Bing,WUWeifeng,YAO Yu.Controller design of electric torque simulator based on internalmodel control［J］.Journal of System Simulation,2009,21(2):122-125.

［7］ YANG Bo,BAO Ran,HAN Huatao.Robusthybrid control based on PD and novel CMAC with improved architecture and learning scheme for electric load simulator［J］.IEEE Transactions on Industrial Electronics,2014,61(10):5271-5279.

［8］ 王明彦,郭犇.基于迭代学习控制的电动伺服负载模拟器［J］.中国电机工程学报,2003,23(12):123-126. WANG Mingyan,GUO Ben.Electric servo load simulator based on iterative learning control［J］.Proceedings of the CSEE,2003,23(12):123-126.

［9］ TINGHSU S,HATTORIS,ISHIDA M,etal.Suppression control method for torque vibration of ACmotor utilizing repetitive controller with Fourier transform［J］.IEEE Transactions on Industry Applications,2002,38(5):1316-1325.

［10］ DOH T,RYOO J.Robustapproach to repetitive controller design for uncertain feedback control systems［J］.Control Theory&Applications,2013,7(3):431-439.

［11］ ZMOOD D N,HOLMESD G.Stationary frame current regulation of PWM inverterswith zero steady-state error［J］.IEEE Transactions on Power Electronics,2003:814-822.

［12］ XIA Changliang,ZHOU Faqiang,WANG Zhiqiang,et al.E-quivalent switch circuit model and proportional resonant control for triple line-voltage cascaded voltage-source converter［J］. IEEE Transactions on Power Electronics,2013:2389-2401.

［13］ CHOU Mingchang,LIAW Changming.Dynamic control and diagnostic friction estimation for an SPMSM-driven satellite reaction wheel［J］.IEEE Transactions on Industrial Electronics,2011,58(10):4693-4707.

［14］ 李毅拓,陆海峰,瞿文龙,等.基于谐振调节器的永磁同步电机电流谐波抑制方法［J］.中国电机工程学报,2014,34 (3):423-431. LIYituo,LU Haifeng,QUWenlong,et al.A permanentmagnet synchronousmotor current suppression method based on resonant controllers［J］.Proceedings of the CSEE,2014,34(3):423 -431.

［15］ 唐诗颖,彭力,康勇,等.并联有源滤波器广义积分控制设计新方法［J］.中国电机工程学报,2011,31(12):40-46. TANG,Shiying,PENG Li,KANG Yong,et al.Novel design procedure of generalized integrators for shunt active power filters［J］.Proceedings of the CSEE,2011,31(12):40-46.

(编辑:张诗阁)

Passive torque servo system based on proportional-resonant control

WANG Zhe, WANGMing-yan, GUO Ben
(School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001,China)

When passive torque servo system is used to simulate load torque,the load torque acted on actuator contains high disturbance torque due to themovement of actuator.In order to realize precise load torque simulation,a novel electric passive torque servo system was proposed,in which proportional resonant controller was added to the outer control loop.By embedding proportional resonant controller with the same frequency,sinusoidal torque signal was tracked with zero steady-state error,and disturbance torque caused by periodicmotion of loaded actuator was restrained effectively;combining with root locus and frequency domain design method,unit proportional resonant controller was put forward to design parameters of controller;moreover,speed feed-forward compensation method was used to reduce impact of disturbance torque acted on system and torque sensor in the beginning.Simulation and experimental results show that20Hz sinusoidal load simulation can be tracked with zero steady-state error and periodic load simulation can be tracked with high precision under dynamic load mode.

permanentmagnet synchronousmotor;passive torque servo system;surplus torque;proportional resonant control; feed-forward control

10.15938/j.emc.2015.09.012

TM 351

A

1007-449X(2015)07-0081-08

2014-09-25

国家自然科学基金(51077025)

王 哲(1985—),男,博士研究生,研究方向为电力电子及电力拖动;王明彦(1957—),男,博士,教授,博士生导师,研究方向为电力电子电能变换技术和电动负载模拟技术;郭 犇(1971—),男,博士,副教授,研究方向为控制理论在电力电子中的应用。

王 哲