基于DFT的同步相量相角测量改进算法研究
2016-08-11唐晓艳
唐晓艳
(福州大学电气工程与自动化学院电气工程系,福建 福州 350116)
基于DFT的同步相量相角测量改进算法研究
唐晓艳
(福州大学电气工程与自动化学院电气工程系,福建 福州 350116)
目前同步相量的相角算法多采用离散傅里叶变换(discrete Fourier transform,DFT),传统DFT算法在非工频情况下的计算精度和实时性不佳。本文分析非同步采样下DFT算法的相角误差,提出一种将2个数据窗的DFT结果进行旋转构造出具有相反相角动态误差分量的相量,以尽可能地削减相角测量的动态误差,最后再进行相角固定误差补偿的改进相角测量算法。与传统相角量测算法相比,该算法较好地修正了相角动态误差,仿真实验结果表明,该算法测量精度高,实时性好,抗干扰能力强。
离散傅里叶;相角测量;同步相量;误差修正
1 引言
20世纪90年代以来电力通信网络得到快速发展,光纤和数字微波已经构成传输网的基础,全球定位系统(GPS)作为统一时钟标准已经在电力系统中使用,对不同电网测量点的电压和电流相角进行同步测量并获得同步相量成为可能。相量可以用来表征系统稳态和暂态的情况[1-2]。相角作为相量要素之一,在同步相量测量中的方法有过零检测法[3]、最小二乘法[4]、小波变换法[5]、DFT算法[6-8]。DFT在同步采样条件下,由于其原理简单,实现方便,对谐波有较好的抑制能力而得到广泛运用,目前是同步相量测量中最常用的方法。
实际电力系统不会始终保持在工频状态,因此DFT会出现非同步采样,此时DFT计算结果无法满足电力系统故障分析对相角精度的要求。针对DFT在非工频情况下精度低的问题,文献[6]的拟正序DFT算法通过虚拟三相坐标合成正序分量以削减动态相角误差,从而减小该部分对相角测量的影响。文献[7]提出的基于偏π/4直角坐标的DFT相角测量算法,对于相角动态误差的削减较文献[6]更多,因此相角测量精度高于拟正序DFT算法。文献[8]通过对在非同步采样下的相角测量值进行固定相角误差和动态相角误差的补偿以得到高精度的测量值,原理简单易行,但该算法难以满足更高精度要求的测量。文献[9]提出了频率自适应的DFT,虽然能够很好抑制信号的谐波、噪声干扰,获得较高精度的相角值,但算法复杂对于用于高实时性要求的场合较难实现。文献[10]的算法虽然原理简单,实现方便,但由于DFT采样数据窗间隔只有一个采样点导致算法容易受到谐波干扰,从而使算法的精度下降。其他文献也对非同步采样下的相角测量进行了研究,得出了大量的有益研究结果,但都存在着需要改进的地方[11-14]。
本文首先对DFT算法在非同步情况下产生误差的机理进行分析,然后通过构建出两个具有相反动态误差分量的相量,将二者结合起来利用改进DFT算法消除相角的动态误差和固定误差。通过大量仿真以及与现有文献中的算法相比较表明,本文提出的算法能较大幅度削减同步相量测量中的相角误差,其精确性和实时性能较好满足电力系统的要求。
2 非同步采样情况下的DFT误差分析
假设一电力信号的采样序列变换如下:
(1)
式中,n=0,1,2,…,N-1,N为一个周期的采样点数,Δλ=Δf/f0为频率偏移率,Δf为频率偏移量,f0=50Hz为额定基波频率,φ为信号初相角。对式(1)进行变换可得其复指数形式为:
(2)
对以上信号进行DFT变换则有:
(3)
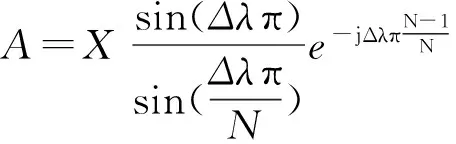
为了便于观察同步相量相角误差情况,可以将式(3)转化为式(4),从式(4)能看出相角误差由固定误差和动态误差两部分组成。
(4)
从式(3)和式(4)我们可以得到非同步采样条件下传统DFT的相量测量误差示意图如图1所示,从而可以进一步分析同步相量测量中相角固定误差和动态误差之间的关系。
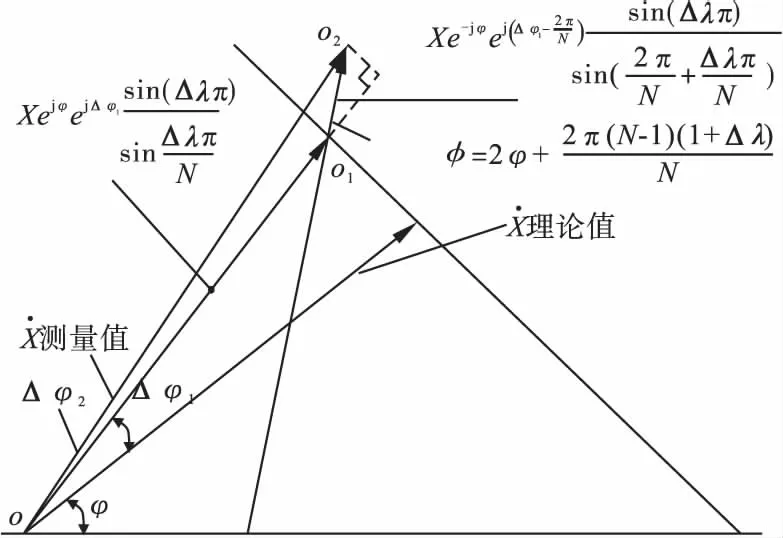
图1 非同步采样条件下DFT的相量测量误差

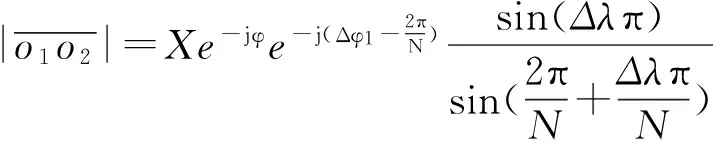

由图1,我们可以得到同步相量相角固定误差为:
(5)
相角的动态误差:
(6)
代入各个相量值,对Δφ2进行化简可得:

(7)
由于实际电网运行时,频率偏移通常在±0.5Hz之间,DFT采样长度N>10,相角动态误差可以进一步化简为式(8)表示:
(8)
综合以上分析,相角固定误差Δφ1与频率偏移率Δλ成正比,通过频率跟踪可以计算出。而动态误差Δφ2是随着初相角φ和频率偏移率Δλ变化的,不容易进行修正和补偿,同步相量测量的相角总误差等于固定误差与动态误差之和,即:
Δφ=Δφ1+Δφ2
(9)
同步相量测量的相角总误差示意图如图2所示。由图2可以看出,如果能削减相角的动态误差,使其尽可能趋近于0,再对计算出的相角进行固定误差补偿,则可以得到精度更高的相量测量相角值。

图2 传统DFT算法的相角总误差(N=32,Δλ=0.1)
3 改进相角算法
(10)
(11)
(12)


(13)
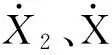
(14)
(15)
因此,式(13)变为:
(16)
在实际电网当中,Δλ非常小,则有:
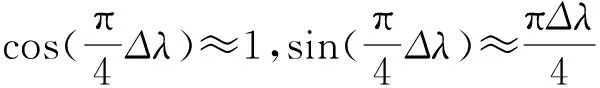
所以式(16)可进一步进行化简:
(17)
观察上式发现相角动态误差增加了一衰减系数πΔλ/4。根据最新国家标准,当系统容量较小时,频率偏差限制允许放宽到0.5Hz[15-17],即Δλ最大值为0.01,相角动态误差可衰减约0.0078倍。且随着Δλ的减小,动态误差的衰减效果越明显。
4 仿真实验
为了验证本文的算法精度,采用MATLAB对多种算法进行仿真分析对比。取采样点数N=32,采样频率1600Hz,标准频率50Hz。由于电网非线性负载的存在,电力信号不可避免地混入谐波干扰,为测试改进算法的抗干扰性,考虑3、5、7次谐波的存在,取被测信号如下:
x(t)=cos(2πft+π/3)+0.06cos(6πft)+
0.04cos(10πft)+0.005cos(14πft)
(18)
表1为不同算法的相角动态误差,由表1可知改进算法与文献[7]的衰减系统相同,且动态误差优于传统算法和文献[6]中算法。但文献[7]的基于偏/4直角坐标的DFT相角测量算法需要4个数据窗的DFT值,而本文只需2个,计算量更小,速度更快。文献[8]算法是直接通过对DFT计算出相角进行固定误差和动态误差补偿,得出最终相角值,其计算精度与动态误差的衰减大小无关,所以在表中没有列出。

表1 不同算法的相角动态误差
图3为传统算法、文献[6-7]算法与改进算法的动态误差比较。从图中可以看出,改进算法与文献[7]中的算法相角动态误差一致,且最大动态误差比文献[6]衰减了约1.5倍,因此本文的算法精度更高。由图3也可知Δλ越趋近于0,相角动态误差削减幅度越大,相角越接近真实值。

图3 不同算法相角动态误差比较
表2为传统算法、改进算法、文献[8]中算法在系统频率为非工频 49Hz、49.5Hz、50.5Hz、51Hz时的相角最大误差,在有谐波干扰的情况下,改进算法和文献[8]的算法都具有良好的抗干扰能力,但改进算法最大相角误差在各个频率处皆小于文献[8]算法,在本次仿真中(被测信号频率f=49Hz),改进算法精度约为文献[8]1.6倍,较传统算法精度提高了约3.5倍,且改进算法只需采用5/4个采样周期,文献[8]则需要2个采样周期,所以改进算法更具有快速性,其测量精度随|Δλ|的减小而提高,其对谐波的抑制能力和抗干扰性优于文献[8]。
图4是传统算法、改进算法、文献[8]中算法在系统频率为非工频49Hz,51Hz时总的相角误差比较图。图中所有算法在相角固定补偿的环节均采用了相同的改进频率跟踪算法,因此各种算法的相角固定误差计算值是相等的。可以看出,改进算法和文献[8]算法的误差较传统算法小,算法精度高,可以满足电力系统要求,但改进算法比文献[8]算法具有更好的实时性能。

表2 三种算法的相角误差
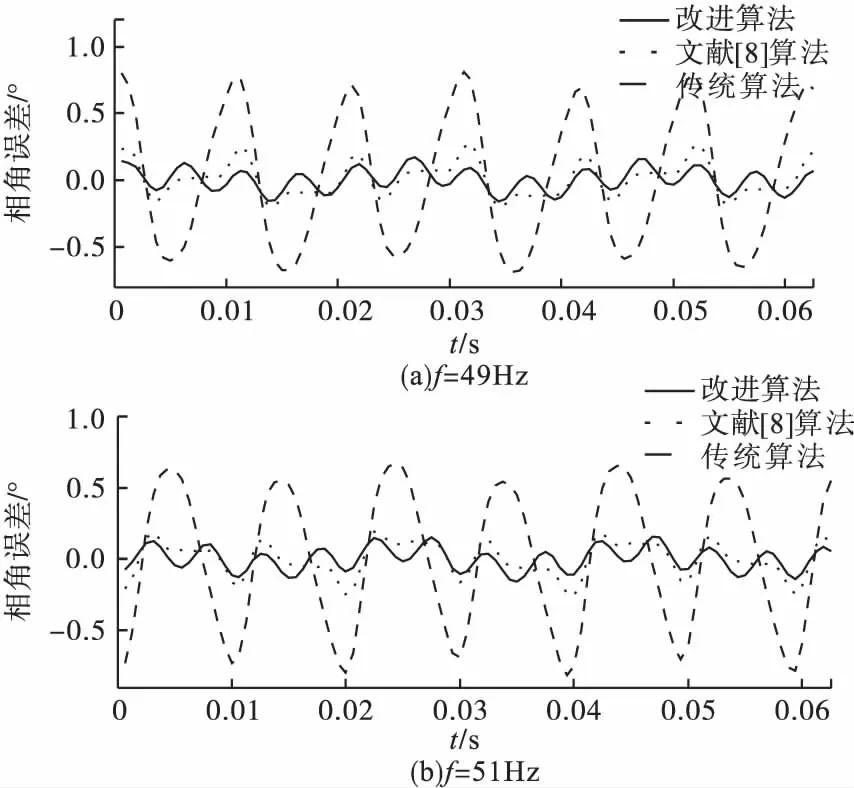
图4 非工频条件下三种算法总相角误差比较
图5展示了被测电力系统信号频率在0.5s处由49Hz突变为51Hz的相角误差图。在频率突变点处,因为各算法在频率跟踪环节的Δλ是由间隔M(一般取M=N)个点的两个数据窗进行DFT计算而出的,所以后面的采样点会影响前面的计算,从而导致Δλ计算不精确,使得相角误差在0.5s后开始出现剧烈波动。改进算法在突变点附近的起伏总体比文献[8]算法与传统算法小,且文献[8]算法在波动处出现尖峰,相角误差远超过系统可容忍误差,同时本文算法约用30ms跟上了实际相角,速率较其他算法快。
现考虑频率跟踪算法对相角测量的影响,采用传统DFT频率跟踪算法和改进频率跟踪算法进行对比。图6为传统算法和本文所提出算法在频率跟踪误差的比较。图7(a)为传统算法在使用不同频率跟踪算法时的相角测量误差,图7(b)为改进算法在使用不同频率跟踪算法时的相角测量误差。图7(c)文献[8]的相角误差。
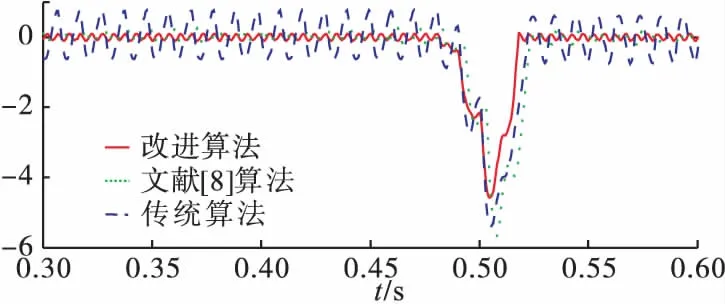
图5 频率突变时相角误差
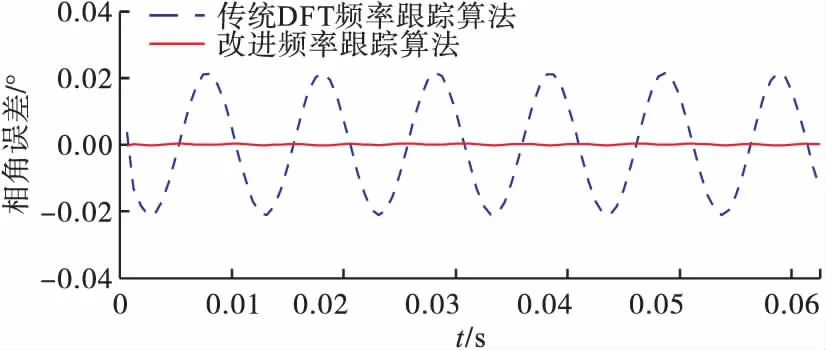
图6 不同算法频率跟踪误差
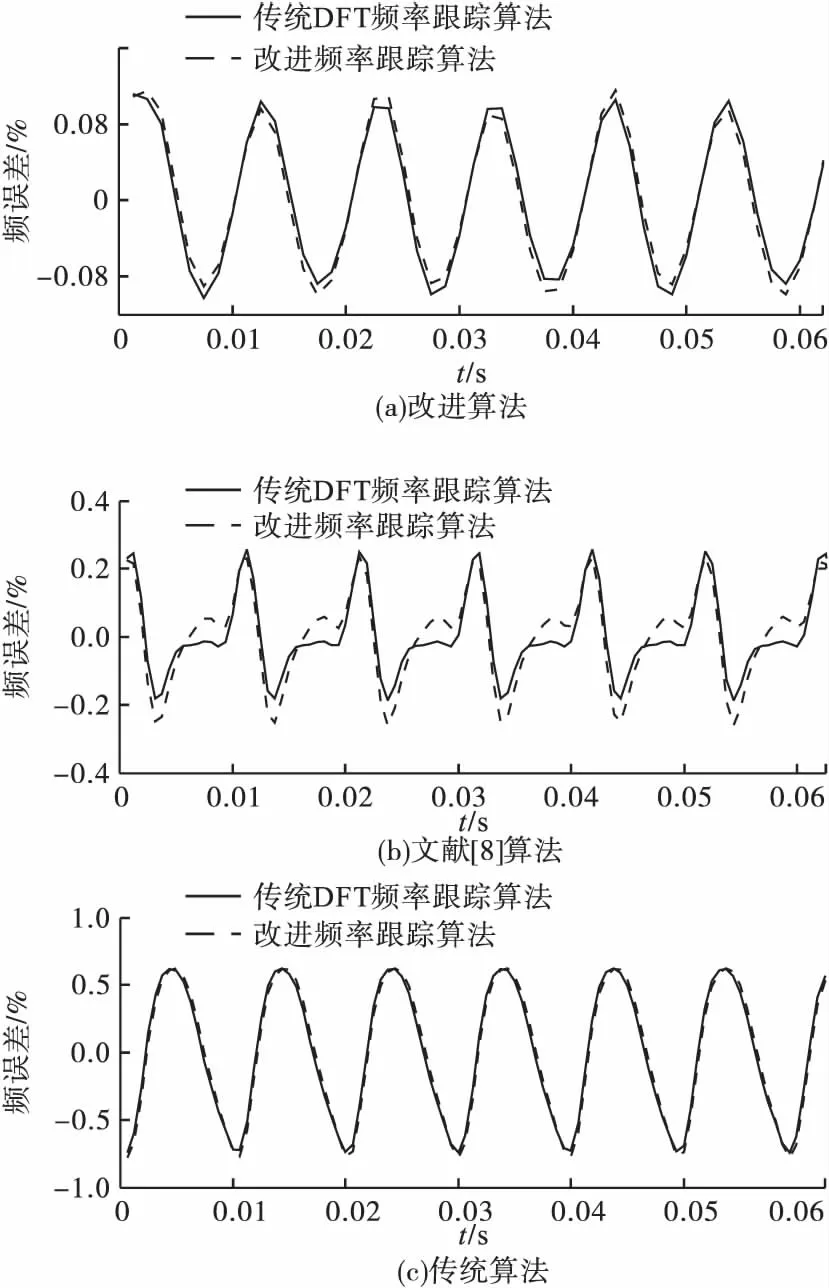
图7 不同频率跟踪算法的相角误差
表3为在不同频率的情况下,采用不同的频率跟踪算法时传统算法和改进算法的最大相角误差。从图中可知,频率跟踪精度提升了约0.02%,本文相角误差减小了约0.01°。相较传统算法,改进算法和文献[8]的算法受到频率跟踪的影响更大,频率跟踪精度越高,同步相量相角测量值就越接近真实值。因此,高精度的频率跟踪算法对于同步相角量测很重要。
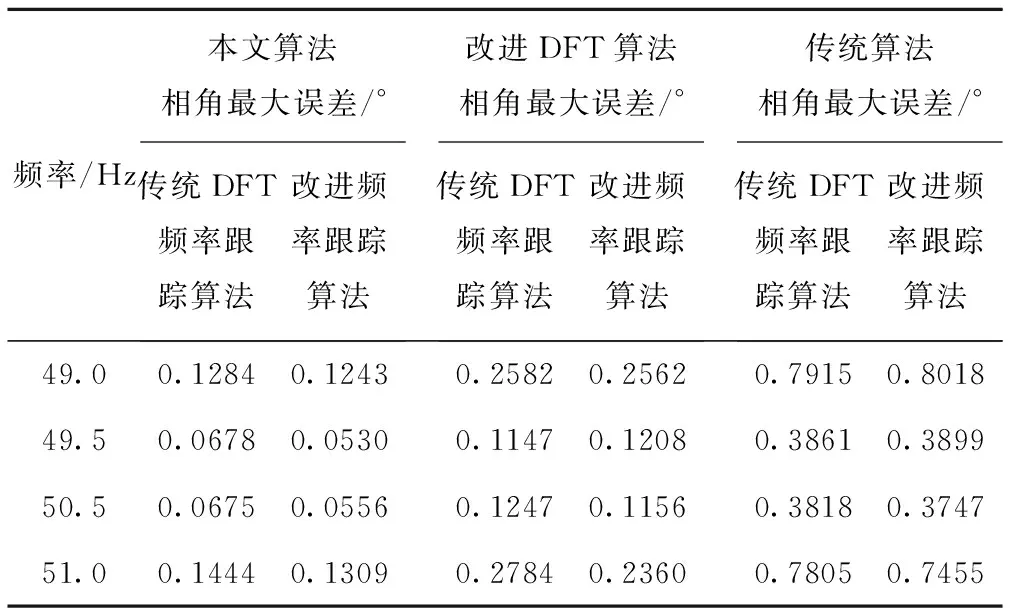
表3 不同算法的相角误差比较
5 结论
本文提出一种将两个数据窗的DFT结果进行旋转和数学运算以尽可能地削减相角测量的动态误差,再通过相角固定误差补偿来获得高精度相角测量值的改进相角测量算法。该方法相比传统算法,相角动态误差得到了良好修正,经固定误差补偿,得到的相角计算值十分接近真实值。通过仿真实验验证了算法在精度、谐波抑制和抗干扰能力与速度上相对传统算法与文献[8]算法有了很大的提升。
[1] 刘友波,刘俊勇,Gareth Taylor,等.面向同步相量轨迹簇规则的电力系统暂态稳定实时评估[J].中国电机工程学报,2011,31(16):32-39.
[2] 任建锋,丁亚伟,付磊,等.基于相位角原理的特高压电网失步解列改进方案[J].电力系统自动化,2011,35(10):104-107.
[3] Vainio O,Ovaska S J.Digital Filtering of Robust 50/60 Hz Zero Crossing Detectors[J].IEEE Transactions on Instrumentation and Measurement,1996,45(2):426-430.
[4] Kamwai,Grondin R.Fast Adaptive Schemes for Tracking Voltage Phasor and Local Frequency in Power System[J].IEEE Transactions on Power Delivery,1992,7(2):789-795.
[5] 杜天军,陈光礻禹,雷勇.基于混叠补偿小波变换的电力系统谐波检测方法[J].中国电机工程学报,2005,25(3):54-59.
[6] Xia Tao,Liu Yilu.Single-phase Phase Angle Measurements in Electric Power System[J].IEEE Transactions on Power Systems,2010,25(2):844-852.
[7] 倪玉玲,郑建勇,梅军,等.基于偏/4直角坐标的DFT相角测量算法[J].电网技术,2014,38(9):2544-2550.
[8] Maohai Wang,Yuanzhang Sun.A Practical,Precise Method for Frequency Tracking and Phasor Eestimation[J].IEEE Transactions on Power Delivery,2004,19(4):1547-1553.
[9] 麦瑞坤,何正友,何文,等.电力系统频率的自适应跟踪算法[J].中国电机工程学报,2009,29(10):52-58.
[10] David Hart,Damir Novosel,Yi Hu,et al.A New Frequency Tracking and Phasor Eestimation Algorithm for Generator[J].IEEE Transactions on Power Delivery,1997,12(3):1064-1073.
[11] Phadke A G,Thorp J S,Adamiak M G.A New Measurement Technique for Tracking Voltage Phasors,Local System Frequency,and Rate of Change of Frequency[J].IEEE Transactions on Power Apparatus and Systems,1983,PAS-102(5):1025-1038.
[12] Begovic M M,Buric P M,Dunlop S,et al.Frequency Tracking in Power Networks in the Presence of Harmonics[J].IEEE Transactions on Power Delivery,1993,8(2):480-485.
[13] Maohai Wang,Yuanzhang Sun.A Practical Method to Improve Phasor and Power Measurement Accuracy of DFT Algorithm[J].IEEE Transactions on Power Delivery,2006,21(3):1054-1062.
[14] Junzhe Yang,Chihwen Liu.A Precise Calculation of Power System Frequency and Phasor[J].IEEE Transactions on Power Delivery,2000,15(2):494-499.
[15] 麦瑞坤,何正友,薄志谦,等.动态条件下的同步相量测量算法的研究[J].中国电机工程学报,2009,29(10):52-58.
[16] 贺春,任春梅.相量测量单元综合矢量误差指标分析[J].电力系统自动化,2012,36(4):110-113.
[17] Dusan Agrez.Dynamic of Frequency Estimation in the Frequency Domain[J].IEEE Transactions on Instrument and Measurement,2007,56(6):2111-2118.
Research on An Advanced Algorithm to Detect Synchronized Phase Angle Based on Discrete Fourier Transform
TANGXiao-yan
(Department of Electrical Engineering,Fuzhou University,Fuzhou 350116,China)
Most methods of phase angle measurements adopt discrete Fourier transform(DFT)algorithm,but traditional DFT algorithm has a bad calculation accuracy and real-time performance in the case of non-power frequency because of asynchronous sampling.This paper analyzed the mechanism of phase angle errors of DFT algorithm under the situation of asynchronous sampling,and proposed an advanced method to improve the performance of phase angle measurements.Through constructing two opposite dynamic phase error components,The paper decreased the dynamic error as much as possible and compensating the constant phase error.Compared with traditional phase angle measurement method,the proposed method can get more accurate phase angle by rectifying the dynamic error and fixing compensation in the synchronous phasor measurement.The accuracy,effectiveness,and real-time performance of the proposed method was proved to reliable by simulations and experiments.
discrete Fourier transform;phase angle measurement;synchronized phasor;error correction
1004-289X(2016)06-0049-06
TM71
B
2015-11-10
