基于自适应陷波滤波器的有源阻尼控制方法

王萍, 蔡蒙蒙, 王尉

(天津大学自动化学院智能电网教育部重点实验室,天津300072)

基于自适应陷波滤波器的有源阻尼控制方法

王萍, 蔡蒙蒙, 王尉

(天津大学自动化学院智能电网教育部重点实验室,天津300072)

LCL滤波器因具有良好的高频衰减特性而被广泛用作并网逆变器与电网的接口。弱电网情况下,并网模型中电网感杭值不可忽略,电网感杭的存在会影响LCL谐振频率的大小,对传统有源阻尼控制方法提出挑战。在分析基于带阻滤波器的有源阻尼控制方案基础上,引入自适应陷波滤波器,提出了一种能够跟随系统参数变化自适应调整陷波滤波器负谐振点位置的有源阻尼控制方法。以光伏逆变系统为载体对该算法进行仿真分析,结果验证了该方法在弱电网情况下的有效性和自适应性:系统谐振频率发生偏移时该方法能够实现对其的准确跟踪,并且显著降低谐振频率点及附近频率段的谐波含量;电网电压发生±5%以内电压突变时,该方法的动态响应特性仍能满足系统的稳定运行要求。

弱电网;并网逆变器;有源阻尼控制;自适应控制;陷波滤波器

0 引 言

分布式发电系统(Distribution Power Generation Systems,DG)包括风力、光伏等新能源发电装置,由于能够在缓解能源危机的同时减少传统化石燃料燃烧带来的温室气体排放而得到大力推广。分布式发电装置等电力电子装置越来越多地接人,向电网添加了大量非线性负载。另外,由于我国风力和光伏能源集中在西北部等较偏远地区,远距离的输电线路不可避免地向电网引人线路阻抗。从而引发了电网谐波污染、电网电压畸变等问题,严重影响电能质量,使电网的条件变得更加复杂。此时电网与电力二次装置联系较弱,即称为弱电网。弱电网情况下的电网仿真模型不再是单纯的稳压交流电源,而应附加一个串联的RL支路来等效代替［1］。

弱电网反过来也会对分布式电源与电网之间的逆变器装置产生影响。文献［2］指出,变化的电网阻抗给逆变器的稳定性、电流控制策略、LCL滤波器的参数设计以及有源阻尼控制方法的适用性等都带来了挑战,本文针对其中的有源阻尼控制方法进行了改善。

目前研究较多的有源阻尼控制方法可以分为以下几类:第一类,单一电流环方案:基于滤波电容电流的有源阻尼反馈［3］、基于滤波电容电压的有源阻尼反馈［4］以及基于滤波电容电压的有源阻尼反馈［5］都属于这一类;第二类,前向通路附加滤波器的方案:例如基于带通滤波器有源阻尼控制［6］;第三类,基于降阶模型的有源阻尼方案:这类方法中典型的应用有分裂电容电流控制法［7-8］;第四类,利用状态反馈法进行闭环设计的方案:对多个状态变量组合并进行加权计算,实现了特征方程的完全配置［9］。然而上述方法都是在LCL参数及电网感抗值唯一确定的情况下才能保证其有效性,弱电网情况下将失去其适应性［10］。

本文针对电网感抗变化带来的谐振点偏移问题,采用自适应陷波滤波器作为突破点,提出了一种能够自适应地改变控制参数,对电网感抗在一定范围内变化的电网情况都有效的有源阻尼控制方法。第一部分对电网感抗与LCL谐振点的关系进行了具体阐述,第二部分分析了基于带阻滤波器有源阻尼控制方法的机理及优缺点,第三部分介绍了自适应陷波滤波器的工作原理,验证了自适应陷波滤波器取代传统带阻滤波器的可行性,第四部分包括系统的整体框图和参数确认,第五部分仿真实验。

1 电网阻抗对LCL谐振点的影响

为了说明电网感抗Lg对LCL谐振频率点的影响,先根据图1推导两者关系。

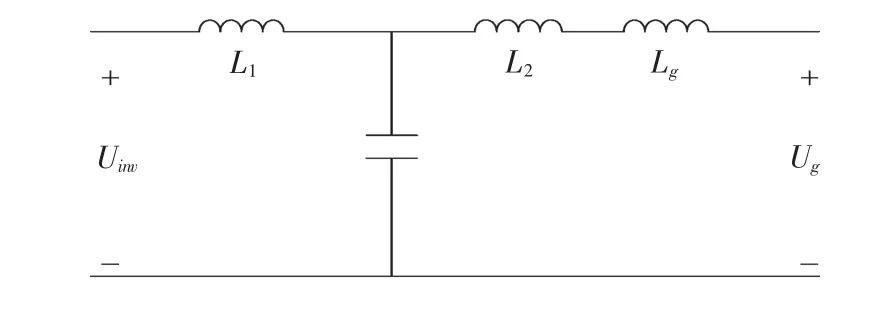
图1 LCL滤波器拓扑Fig.1 Topology of LCL filter

图1 所示,电网感抗的加人相当于在LCL网侧串人一个附加电感,因此谐振频率点的推导公式改写为:

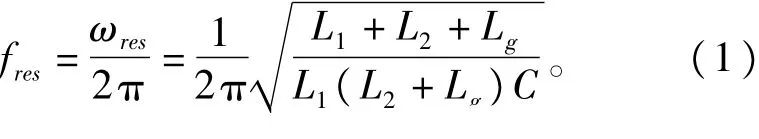
由式(1),Lg的变化将直接影响谐振频率的大小,当Lg在0 mH到1.5 mH之间变化时,谐振频率随Lg变化的曲线如图2所示。可知fres与Lg成负相关关系,fres随Lg的增大而逐渐降低。

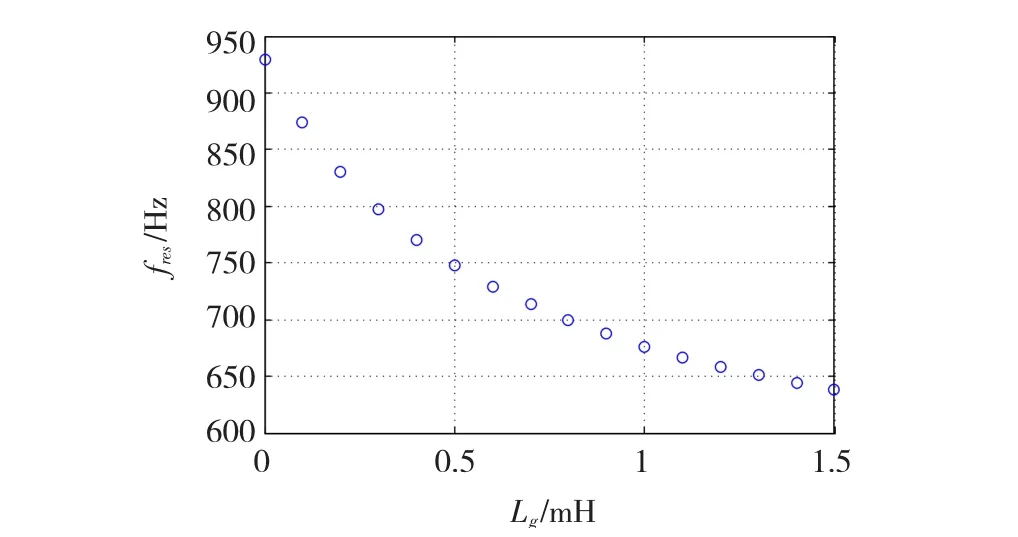
图2 Lg与fres的关系曲线Fig.2 Relation curve between Lgand fres

2 基于带阻滤波器的有源阻尼控制方法

LCL滤波器因对开关频率以上高次谐波具有很好的抑制效果而被广泛用作光伏并网逆变器与电网的接口,但它的存在同时增加了系统阶数,带来了谐振尖峰问题,对系统的控制策略提出了更加严格的要求。常用的抑制谐振增加系统阻尼的方法分为两类:无源阻尼和有源阻尼控制方法。前者较为简单,但会产生不必要的损耗,降低系统效率［11］,因此大功率光伏并网系统中通常采用有源阻尼控制方法。

常用的有源阻尼控制方法通过对含有谐振尖峰的环节G(s)添加一个H(s)反馈环节进行反馈校正实现［11］。

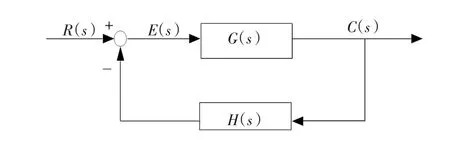
图3 典型的反馈系统Fig.3 Typical feedback system

图3 所示为典型反馈系统的控制原理,当反馈环节满足谐振频率附近处1+G(jωres)H(jωres)实部大于零,即可实现谐振尖峰的抑制。由于谐振频率处网侧电感、逆变器侧电感以及滤波电容处的电流电压信号相位变化范围各不相同［12］,反馈信号所取不同时需采用的反馈环节也相应发生改变,以实现相位的超前滞后,最终使得1+G(jωres) H(jωres)在一、四象限范围内。

然而,实际应用中通常需要考虑采样延时和计算延时的影响(相当于在反馈环节中附加了惯性延迟环节),这些非理想因素虽然不会导致系统的失稳,但却会影响有源阻尼控制的有效性。为避免此影响,本文考虑在前向通道G(s)中直接加人校正环节的有源阻尼控制方法。

具体控制框图如图4所示,参照文献［6］所提出的基于带通滤波器的有源阻尼控制方法,用带阻滤波器来替代带通滤波器实现同样功能,在不额外增加传感器的前提下,将带阻滤波环节添加在调制波发生环节之前,实现一种基于带阻滤波器的有源阻尼控制方法。

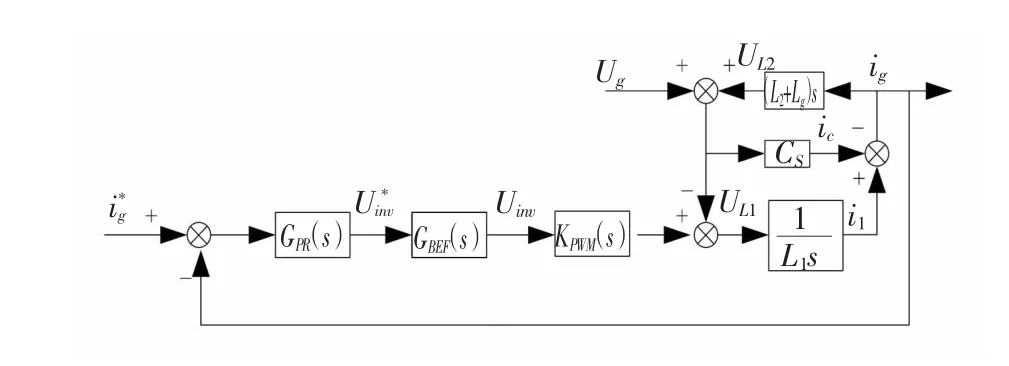
图4 基于带阻滤波器的有源阻尼方案Fig.4 Band-reject filter based active dam ping control strategy

从图中可以看出,前向通道中原本经由PR电流调节器输出的调制波U*inv,再通过带阻滤波器的调节输出最终的调制波Uinv,送给PWM波发生模块。对电网侧的电流进行采样,再通过一个单位反馈构成闭环,就形成了整个控制策略。

由此可以推导出整个系统的开环传递函数:

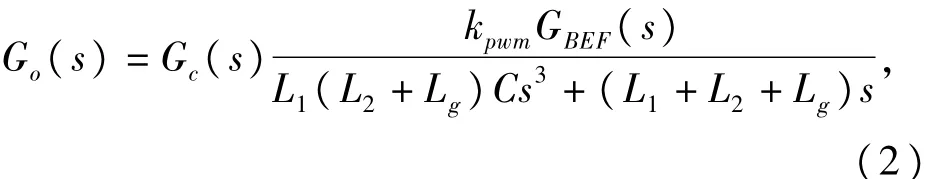
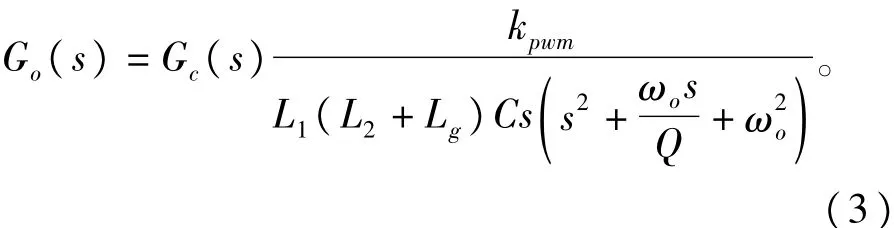
根据式(2)、式(3)绘制带阻滤波器加人前后的系统开环波特图,用作对比分析,如图5所示。

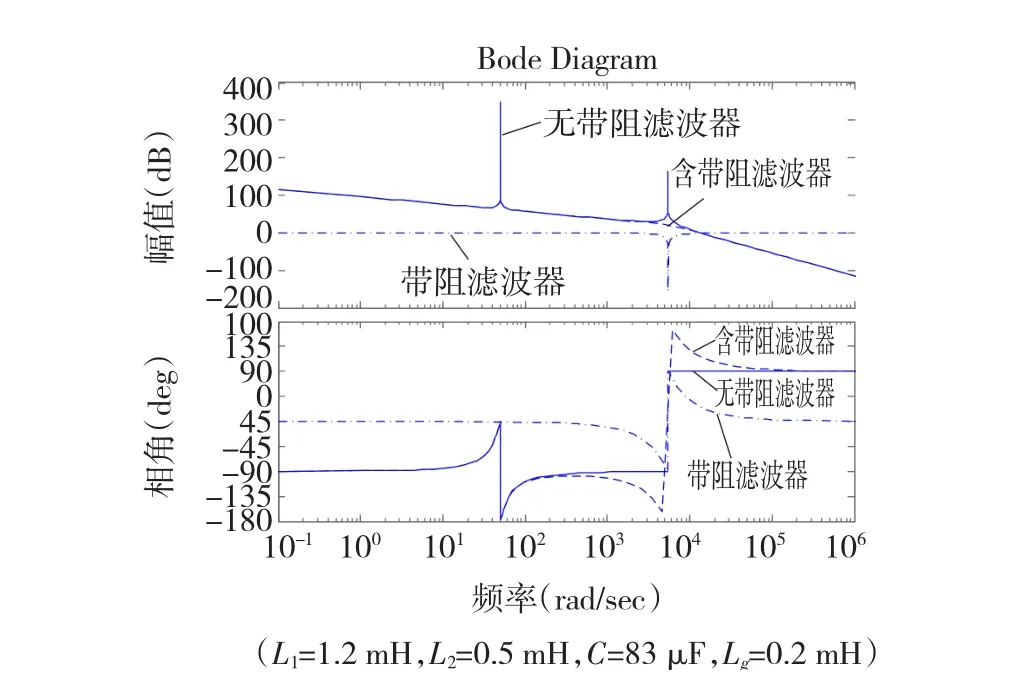
图5 系统波特图Fig.5 System bode plot

对比图中三条曲线,可以看出,直线代表的没有加人带阻滤波环节的原系统波特图中存在一个十分明显的谐振尖峰,点划线所示带阻滤波器环节在同一频率处产生了一个负的谐振尖峰,与之叠加使得原系统中的谐振尖峰得到抵消,由此,虚线所示加人带阻滤波环节后的控制策略下的系统不再存在尖峰等不稳定因素。另外,如图直线和点划线所示,系统低频和高频开环增益受到带阻滤波器的影响很微弱,可以忽略不计,说明了其引人并不会破坏LCL滤波环节对高频信号的抑制效果,同时也保持了PR控制器对基频信号的良好跟踪效果。最后,从相位特性上看,原系统中由LCL环节引人的共轭极点所引发的谐振频率处180°相位突变也得到了改善。

图6为带阻滤波器加人前后的系统闭环零极点分布图。图6(a)所示加人有源阻尼控制前系统具有分布在正半实轴的极点,说明此时系统是不能稳定的。加人带阻滤波器后系统零极点分布如图6(b)所示,原本给系统带来不稳定因素的共轭极点进人负半轴区域,并且,从距离虚轴的位置可以看出,与主导极点相比,该极点的影响可以忽略不计。系统的主导极点在加人带阻滤波器环节后没有发生偏移,说明带阻滤波器环节不会改变系统的动态响应速度以及阻尼特性。由此,本方法的有效性得到了理论上的支持。

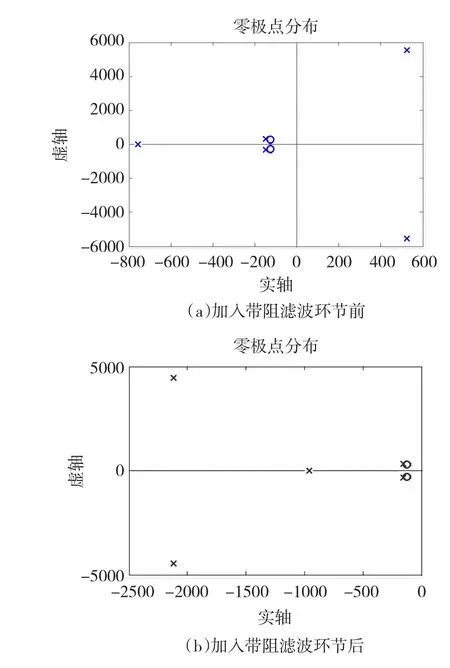
图6 系统闭环零极点分布Fig.6 System zero-pole distribution

保持PR控制器参数以及GBEF参数不变,Lg取值变化为0.3mH,系统波特图有所改变,如图7所示。

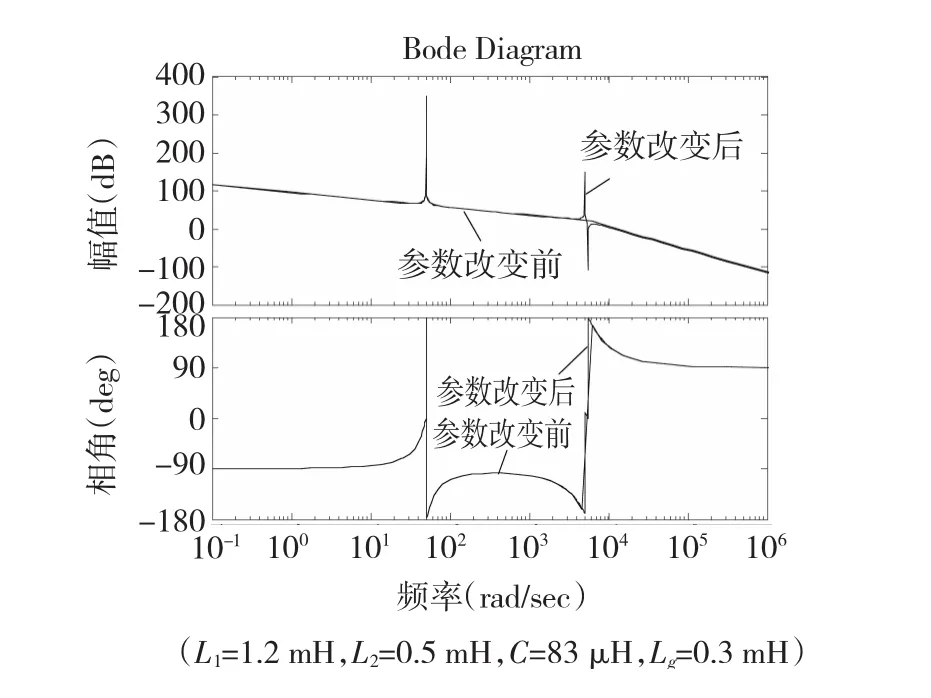
图7 Lg参数发生改变时的系统波特图Fig.7 System bode p lot w ith a changed Lgvalue

图中原系统中的谐振尖峰发生偏移,不能被带阻滤波器产生的负谐振尖峰抵消,有源阻尼控制失效。因此传统基于带阻滤波器的有源阻尼控制方法存在其局限性。

光伏逆变器接人点的改变必然会引起等效电网感抗值的变化,并且,随着分布式发电系统越来越多的接人到电网当中,同一接人点的电网感抗值也不是一成不变的,因此,构建一种能够适应一定范围内电网感抗变化的有源阻尼控制方法十分重要。

3 自适应陷波滤波器

上节提到电网感抗发生改变时,传统基于带阻滤波器的有源阻尼控制方法失去适应性,因而这里考虑引人在声学去噪领域应用广泛的自适应陷波滤波器,用它来代替传统带阻滤波环节,实现随谐振点偏移而自适应调节参数的有源阻尼控制方法。

下面介绍自适应陷波滤波器的基本工作原理,参照图8进行分析［13］。

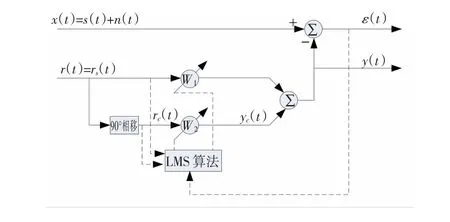
图8 自适应陷波滤波器原理Fig.8 W orking princip le for adaptive notch filter

图中x(t)为输人信号,即叠加有干扰信号的原始信号,s(t)为目标信号,n(t)为需要滤除的干扰信号,rs(t)=A sinωot为参考信号,是一个同干扰信号相关的纯正弦信号,参考信号90°相移后得到rc(t),rc(t)与rs(t)进行加权运算得到y(t),ε(t)为自适应陷波滤波器的输出信号,也就是对原始信号特定频率谐波滤除后的信号,其值等于原始信号x(t)与加权值y(t)的差。

LMS模块的作用是对加权值W1、W2进行迭代更新,其中rs(t)、rc(t)、ε(t)作为输人信号输人到LMS算法模块中,W1(t)、W2(t)作为模块的输出,内部采用最小均方的迭代算法(LMS算法),目的是使误差信号ε(t)的功率ε2(t) 趋于极小值,套用文献［14］中的公式,权函数迭代方法如下:

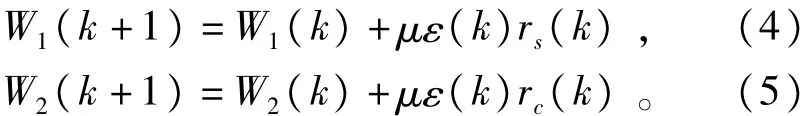
其中μ代表自适应迭代步长,k为与时间相关的迭代序列,并有t=kτ,τ为采样时间间隔。

文献［14］同时推导出了自适应陷波滤波器的等效传递函数,表达式如下:

对比发现式(6)与前文所介绍带阻滤波器的传递函数具有相同形式,对频率为ωo/2πHz的信号同样具有无穷大衰减功能,令μA2/τ=ωo/Q,则自适应陷波滤波器可以完全等效为中心频率ωo的带阻滤波器。与带阻滤波器类似,μA2取值越大,相应的品质因数就越小,系统的带宽就越大。因此可以通过优化μA2的取值来改善陷波滤波器的响应特性。由于自适应陷波滤波器的中心频率即参考信号频率易于更改,改变参考信号频率可灵活地对陷波滤波器的中心频率进行调整,实现滤波器在干扰信号频率改变时的自适应性,因此能够满足一定变化范围电网感抗条件下的有源阻尼控制要求。

4 总体系统框图及参数设置

4.1 总系统框图

上文给出了一种基于带阻滤波器的有源阻尼控制方法,同时证明了采用自适应陷波滤波器代替带阻滤波器可以实现有源阻尼控制的自适应性。

在此基础上,可以得出本文的最终控制策略——基于自适应陷波滤波器的有源阻尼控制方法。总体控制框图如图9所示,这里电流环采用准PR控制方法。

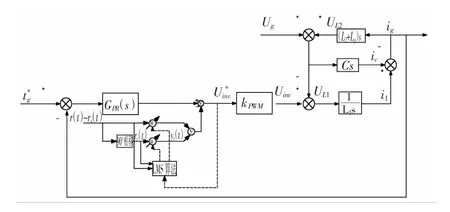
图9 基于自适应陷波滤波器的有源阻尼控制方案Fig.9 Adaptive notch filter based active damping control system fram ework

4.2 自适应滤波器参数设置

为了更好地实现并网电流跟踪及有源阻尼控制的效果,下面对控制器参数的选取方法进行简要分析。由于本文主要研究对象为自适应陷波控制器,因而准PR控制器参数的选取在这里不作为重点,下文针对自适应陷波滤波器的主要参数:收敛因子μ、迭代步长τ进行说明。

首先分析迭代步长τ对系统动态响应速度的影响。为观察方便,我们可以将目标信号设置为谐波成分较为简单的:s(t)=sin(2πt)+sin(2π×2t)+ sin(2π×5t),叠加上n(t)=0.1cos(2π×50t)的干扰信号后作为原始信号输人到自适应陷波滤波器中,改变τ值,观察不同步长τ下系统的响应结果,如图10和图11所示,分别对应了τ=3×10-4s(图10)以及τ=3×10-3s(图11)时的系统。仔细观察可以发现图11中的输出信号比图10中的收敛要慢,收敛时间更长。由此可以得出步长越短,收敛速度越快的结论。然而为减小自适应迭代权噪声,步长的选取又不能过分小,本实验选取τ=1×10-5s。

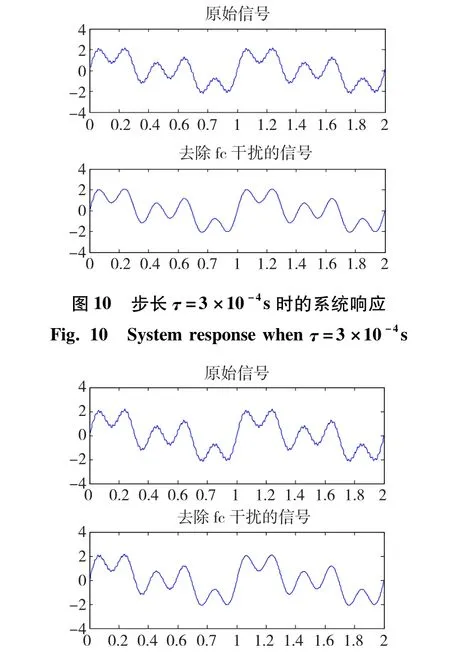
图11 步长τ=3×10-3s时的系统响应Fig.11 System response whenτ=3×10-3s

确定了τ的取值后,下面分析迭代因子μ的选取原则,图12、图13分别给出了不同μ值下的系统开环波特图及阶跃响应曲线,反映了μ值的选取对系统动静态特性的影响。图12所示,各μ值下的系统低频段和高频段开环幅相曲线基本重合,只在谐振频率附近存在差异。并且μ值越大,开环增益越小,带宽越宽,对谐振频率点及附近谐波含量的抑制效果也越明显,因此可以推断出μ值越大,谐振频率点发生微小偏移时的有源阻尼控制效果就越能得到保证。然而,如图13所示,当μ=0.01或0.008时,系统的单位阶跃响应虽能收敛,但却出现了叠加的新低次谐波,这个现象说明μ的取值也并非越大越好。当μ分别取为0.02、0.03、0.05、0.08时,系统单位阶跃响应的超调量逐渐增大,收敛速度却没有太大的差别。因此,这里选取超调量较小且不会给系统引人新谐波的0.02作为收敛因子μ的取值。

图12 不同μ值下的系统开环波特图Fig.12 System open loop bode plot under differentμvalue

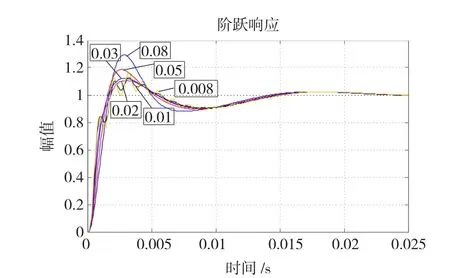
图13 不同μ值下的系统阶跃响应Fig.13 System step respond under differentμvalue

这样τ,μ,A的取值都得到了唯一的确定,但是回过头再来考虑该等式μA2/τ=ωo/Q时,却会发现一个问题:若保持τ,μ,A的取值不变,当ωo因为弱电网特性下等效电网感抗的改变而发生偏移时,为保证系统的Q值不变,τ,μ,A的取值也应该做同比例放大或缩小。因此选择上述仿真中对应的ωref= 133作为基准频率,令kω=ωo/ωref,仍然忽略τ,A对系统动静态特性的影响,在自适应调整陷波滤波器中心频率ωo的同时调整μ的取值为kωμ。由此附加有参数自适应校正环节的总系统有源阻尼控制方案唯一确定,具体的参数校正实现由LMS算法的软件编程完成。

5 仿真验证

上文确定了系统的整体控制框图及参数,下面通过Matlab/SIMULINK平台搭建7kVA光伏逆变系统仿真模型以验证本文所提方法的有效性。图14给出了系统拓扑结构。

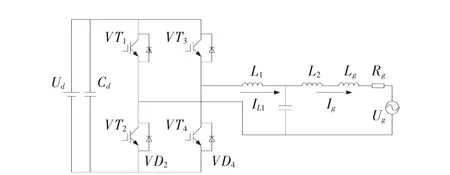
图14 光伏并网逆变器拓扑Fig.14 PV grid-connected inverter system topology

系统参数设置参照表1,其中PWM波形的发生采用双极性调制方法,自适应陷波滤波器中的LMS算法模块通过自定义编写S-function模块实现。按照表1的参数进行仿真设置,得出如图15所示的仿真结果。

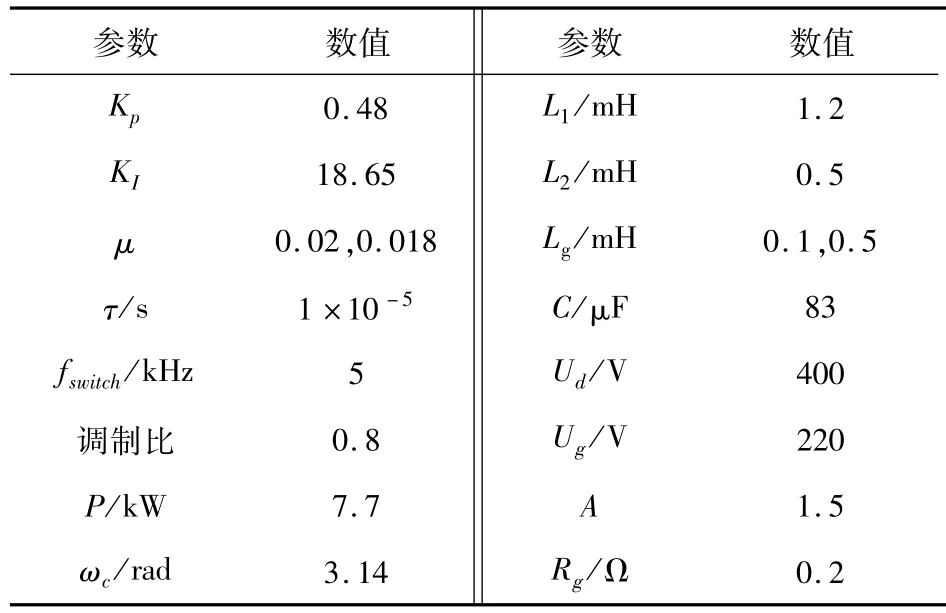
表1 系统参数Table 1 System parameters

图15(a)中并网电流在3/4个基波周期后跟踪上电网电压相位,并一直保持了对电网相位的跟随,满足了逆变器并网单位功率因数运行的要求。图15(b)为逆变器直接输出的逆变器侧电感电流,其波形相较于图15(a)明显多出大量开关频率次谐波,对比两图,又可以验证LCL滤波器对高次谐波的优良的抑制效果。

为充分验证该方法的有效性及自适应性,本文选取了两组不同控制条件下的并网电流FFT数据结果,并进行对比分析:第一组通过对比自适应陷波滤波器加人前后系统并网电流中谐振频率谐波含量的大小,验证了其有效性;第二组则通过对比电网感抗发生改变情况下传统基于带阻滤波器的有源阻尼控制方法及基于自适应陷波滤波器的有源阻尼控制方法的有效性,验证了其自适应性。

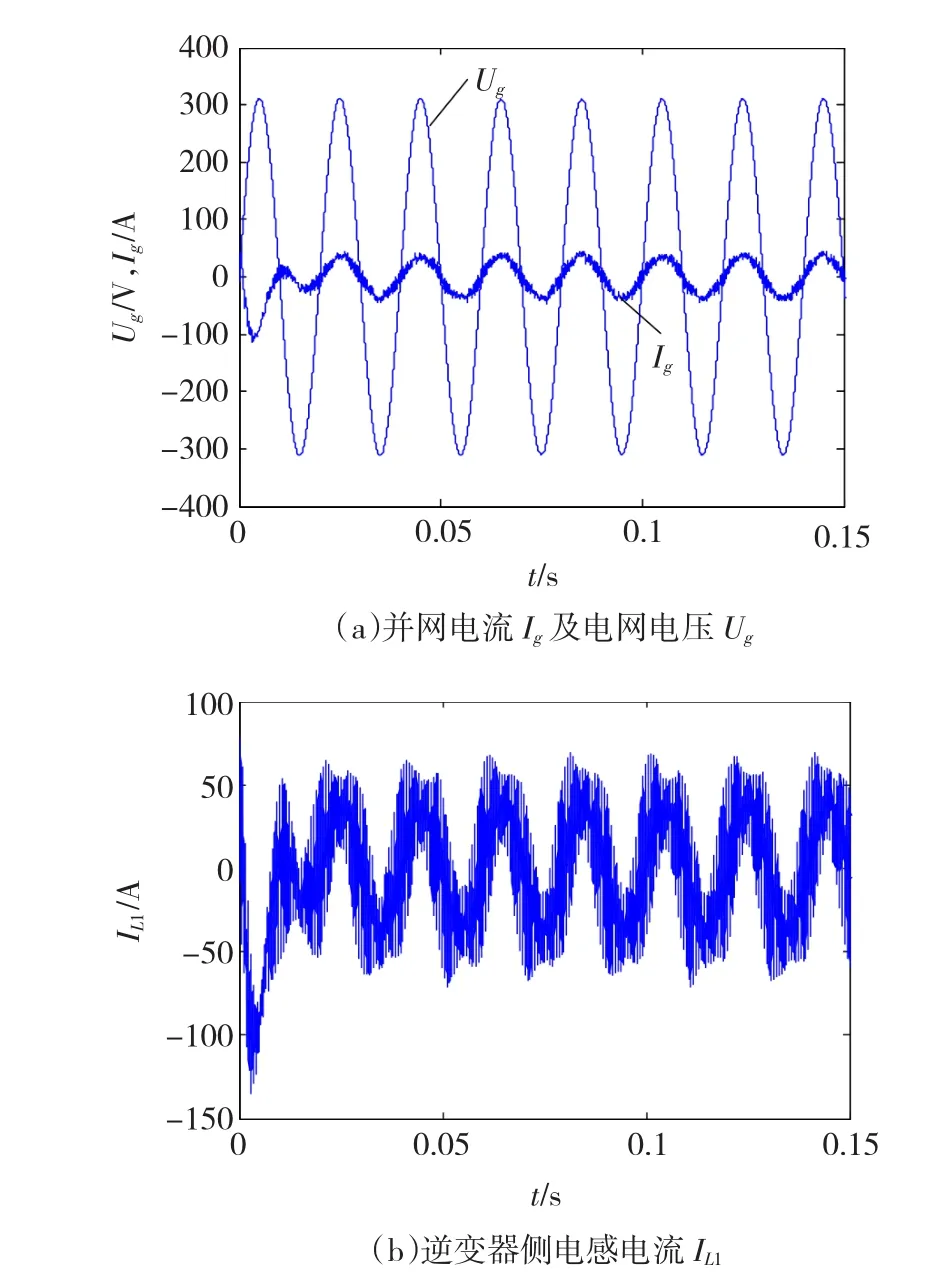
图15 并网电流Ig的跟踪效果以及LCL滤波器滤波效果Fig.15 Tracking accuracy of the current Igand LCL filter filtering effect IL1

5.1 有效性验证

图16、图17分别为加人自适应陷波滤波器有源阻尼控制模块前后的系统并网电流频谱分析图,对比可知,系统谐振频率(873.48 Hz)处以及附近频率的谐波含量在采用该有源阻尼控制方法后大幅下降。同时表2列出了两种情况下的具体谐波含量值,对比也可以看出该方法对谐振频率附近的谐波具有明显抑制效果,从而验证了该方法的有效性。

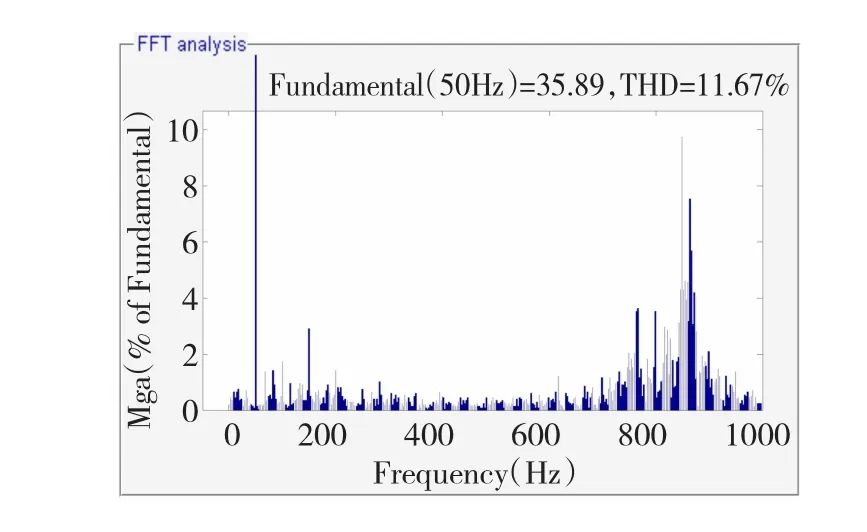
图16 并网电流IgFFT(无有源阻尼)Fig.16 Grid-connected current IgFFT(w ithout adopting active dam ping control)

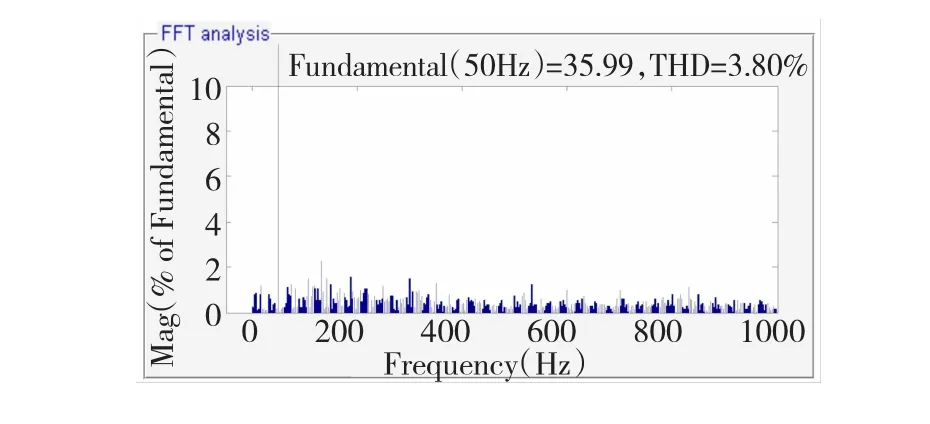
图17 并网电流IgFFT(含自适应有源阻尼)Fig.17 G rid-connected current IgFFT(adopting active damping control)

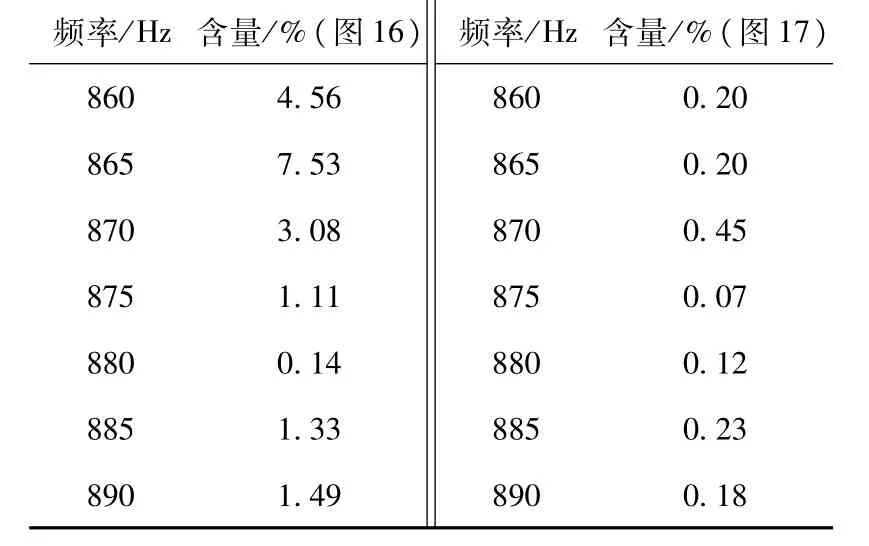
表2 谐波含量对比Table 2 Harm onic contents com parison

5.2 自适应性验证

改变系统参数,使Lg从0.1 mH变化为0.5 mH,理论推导得出此时的系统谐振尖峰应偏移到748 Hz处。分别观察无有源阻尼控制方法,传统有源阻尼控制方法以及自适应陷波滤波器有源阻尼控制方法的控制效果。仍采用对并网电流谐振频率附近含量的抑制效果来衡量控制方法的有效性,得出图18～图20所示结果,分别表示无阻尼控制,传统阻尼控制,以及自适应有源阻尼控制结果。为更清晰地对比图19、图20的仿真效果,将图19与图20所对应具体谐波含量的数值表示列于表3中。

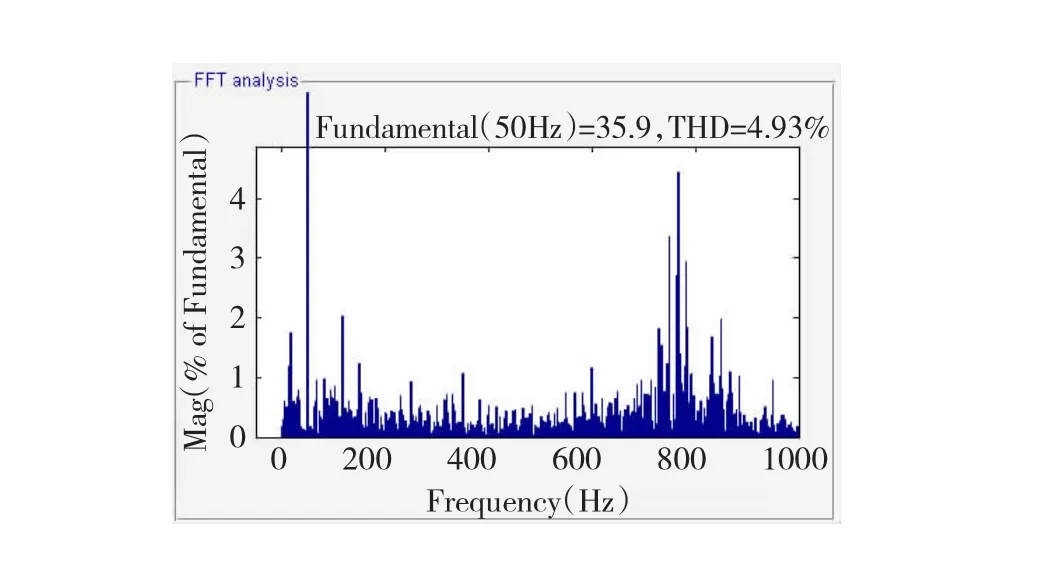
图18 无有源阻尼控制仿真结果Fig.18 Control result w ithout adopting active damping

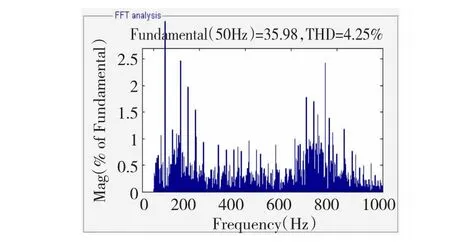
图19 传统有源阻尼控制仿真结果Fig.19 Control resu lt w ith traditional active dam ping

图20 自适应有源阻尼控制仿真结果Fig.20 Control result w ith adaptive active dam ping

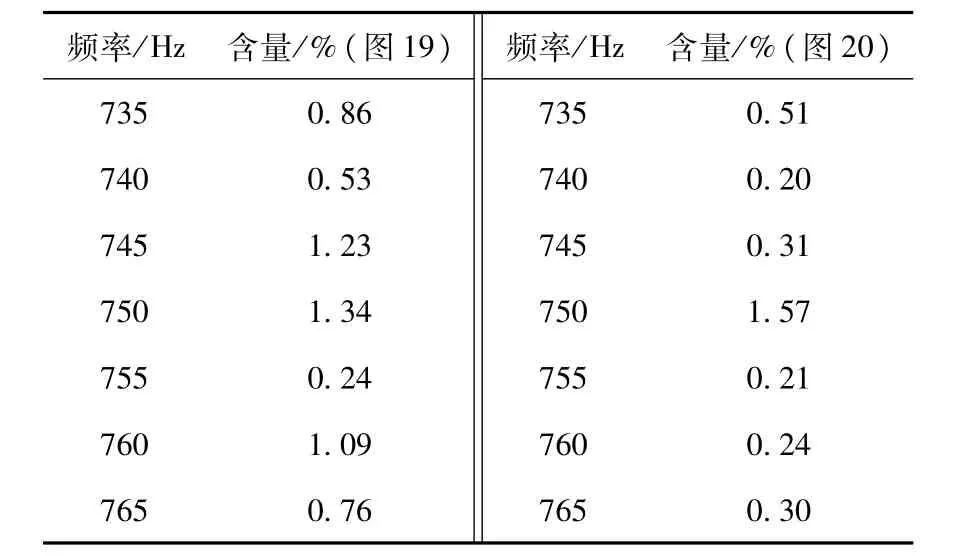
表3 谐波含量对比Table 3 Harmonic contents comparison

对比图18与图16不难发现,电网电感值的波动导致了系统谐振尖峰的偏移,新的谐振被显示于748 Hz附近频率段,呼应了前文电网感抗对电网电流高频段影响的分析。

纵向对比完图18、图16对应两组电网感抗值下的系统响应后,再来对比分析电网感抗发生变动时两种控制方法的谐振抑制效果,即验证传统有源阻尼控制方法及自适应有源阻尼控制方法的自适应性。

首先可以肯定的是,图19及图20中748 Hz附近的谐波含量相较图18都存在明显下降,而图19中748 Hz附近的谐振含量仍然高于其他频率,呈现出较弱的谐振现象。相较之下,图20中748 Hz附近频率段的谐波含量下降趋势更为突出,下降后基本与其他频率段持平,谐振尖峰完全消除。表3中的实验数据也再次支持了这一实验结果,佐证了自适应有源阻尼控制方法较传统有源阻尼控制方法具备对新谐振尖峰更突出的抑制效果。

综上所述自适应控制算法能够在电网参数发生变化时及时调整自身参数从而表现出更为优越的性能,而传统阻尼控制方法则不具备这一自适应特性。

5.3 电网条件突变时的系统动态响应特性

验证完基于自适应陷波滤波器有源阻尼控制方法的有效性和自适应性能之后,分两种情况来考察自适应控制方法的动态响应特性:第一种是电网电感发生瞬时突变的情况,第二种是理想电网负载突变的情况。设置0.1 s时刻,电网电感由0.1mH变化为0.5mH,得出相对应输出并网电流的波形如图21所示。

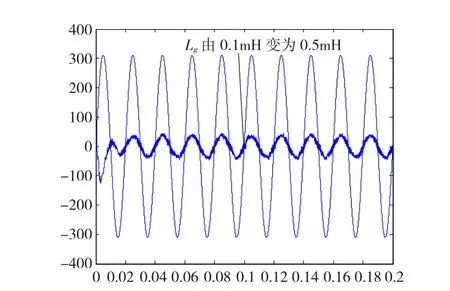
图21 电网感抗突变下的动态响应Fig.21 Dynam ic response w ith a sudden im pedance change

由图21可知,系统参数突变时,自适应有源阻尼控制可以迅速做出调整并达到稳定收敛的结果,调整过程当中并不会导致失稳或超调现象,证明了自适应有源阻尼控制方法良好的动态响应特性。

下面再来考虑电网负载突变的情况,实际电网电压运行的最大变动范围为±5%,因此这里将电网电压做如下设置:0.1 s时由220 V跳变成231 V,0.2 s时由231 V越变为209 V。如果系统能够满足该条件下的电网负载波动,则电网的正常运行要求也能得以满足,仿真结果如图22所示。

如图22所示,随着电网电压的波动,并网电流整体保持稳定,仅在0.1 s及0.2 s时刻后的半个周期内存在小幅波动,但是波动范围很小,动态响应过程较短,能够满足系统稳定性的要求,对电网造成的不良影响基本可以忽略。

综上所述,在电网参数发生突变时,本文提出的基于自适应陷波滤波器的有源阻尼控制方法能够同时满足系统的动稳态特性要求。

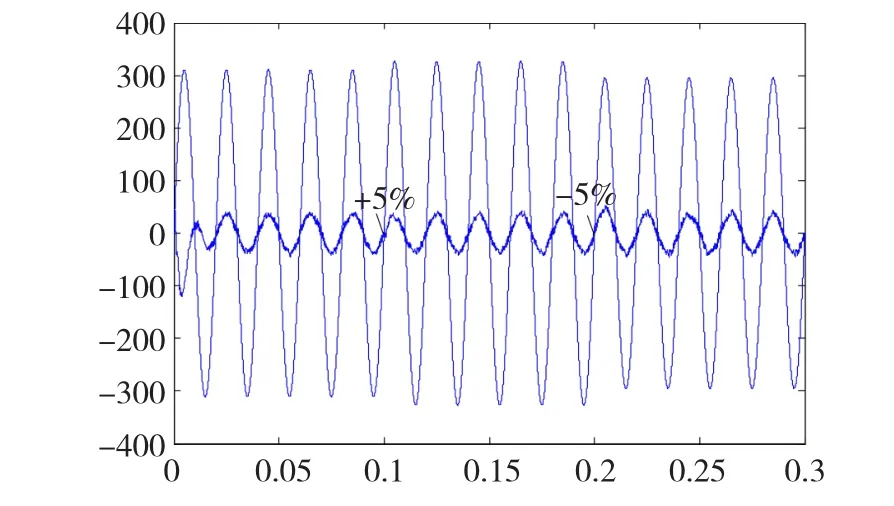
图22 电网负载波动下的动态响应Fig.22 Dynam ic response w ith a sudden grid-voltage change

6 结 论

本文分析了光伏逆变系统中电网感抗对于LCL谐振点的影响,在基于带阻滤波器的有源阻尼控制方法基础上,引人自适应陷波滤波器,提出了一种能够跟随电网感抗值变化自适应调整控制参数的有源阻尼控制方法,分析了其控制机理,并通过7kVA的光伏逆变系统仿真模型验证了该方法的有效性及自适应性,得出了如下结论:

1)随着电网感抗值的波动,LCL谐振频率呈负相关变化;

2)自适应陷波滤波器能够代替带阻滤波器实现衰减特定频谱段波形的作用;

3)自适应陷波滤波器的参数τ与收敛速度相关,参数μ与系统带宽以及动态响应的收敛性相关;

4)该基于自适应陷波滤波器的有源阻尼控制方法能够很好的满足弱电网情况下的动稳态响应要求。

该有源阻尼控制方法原理简单,但是需要以对电网感抗值的准确测量为前提,额外增加了电网感抗在线测量的技术成本。但其控制结构简单,容易实现,并且提高了电网的适应性,具有一定的应用前景和发展空间。

［1］ 鲁力,刘芳,张兴,等.弱电网条件下单相光伏并网逆变器的控制研究［J］.电力电子技术,2012,46(5):36-38. LU Li,LIU Fang,ZHANG Xing,etal.Study of controlling a single-phase photovoltaic grid-connected inverter operating in a weak grid［J］.Power Electronics,2012,46(5):36-38.

［2］ LISERRE M,TEODORESCU R,BLAABJERG F.Stability of photovoltaic and wind turbine grid-connected inverters for a large set ofgrid impedance values［J］.IEEE Transactionson Power E-lectronics,2006,21(1):263-272.

［3］ 王斯然,吕征宇.LCL型并网逆变器中重复控制方法研究［J］.中国电机工程学报,2010,30(27):69-75. WANG Siran,LÜZhengyu.Research on repetitive controlmethod applied to grid-connected inverterwith LCL filter［J］.Proceedings of the CSEE,2010,30(27):69-75.

［4］ TWINING E,HOLMESD G.Grid current regulation of a threephase voltage source inverter with an input LCL filter［J］.IEEE Transactions on Power Electronics,2003,18(3):888-895.

［5］ MALINOWSKIM,BERNET S.A simple voltage sensorless active damping scheme for three-phase PWM converters with an LCL filter［J］.IEEE Transactions on Industrial Electronics,2008,55 (4):1876-1880.

［6］ 尹靖元,金新民,吴学智,等.基于带通滤波器的LCL型滤波器有源阻尼控制［J］.电网技术,2013,37(8):2376-2382. YIN Jingyuan,JIN Xinmin,WU Xuezhi,et al.Active damping control strategy for LCL filter based on band pass filter［J］.Power System Technology,2013,37(8):2376-2382.

［7］ SHEN Guoqiao,XU Dehong,CAO Luping,et al.An improved control strategy for grid-connected voltage source inverters with an LCL filter［J］.IEEE Transactions on Power Electronics,2008,23(4):1899-1906.

［8］ 沈国桥,徐德鸿.LCL滤波并网逆变器的分裂电容法电流控制［J］.中国电机工程学报,2008,28(18):36-41. SHEN Guoqiao,XU Dehong.Current control for grid-connected inverters by splitting the capacitor of LCL filter［J］.Proceedings of the CSEE,2008,28(18):36-41.

［9］ GABE IJ,MONTAGNER V F,PINHEIROH.Design and implementation of a robust current controller for VSI connected to the grid through an LCL filter［J］.IEEE Transactions on Power Electronics,2009,24(6):1444-1452.

［10］ YANG Shuitao,LEIQin,PENG F Z,et al.A robust control scheme for grid-connected voltage-source inverters［J］.IEEE Transactions on Industrial Electronics,2011,58(1):202-212.

［11］ 郭小强,邹伟扬,顾和荣,等.并网逆变器LCL接口直接输出电流控制建模及稳定性分析［J］.电工技术学报,2010,25 (3):102-109. GUO Xiaoqiang,WU Weiyang,GU Herong,et al.Modelling and stability analysis of direct output current control for LCL interfaced grid-connected inverters［J］.Transactions of China Electrotechnical Society,2010,25(3):102-109.

［12］ 许津铭,谢少军,肖华锋.LCL滤波器有源阻尼控制机制研究［J］.中国电机工程学报,2012,32(9):27-33. XU Jinming,XIE Shaojun,XIAO Huafeng.Research on control mechanism of active damping for LCL filters［J］.Proceedings of the CSEE,2012,32(9):27-33.

［13］ 惠俊英,蔡平,马晓民.自适应陷波滤波器的应用研究［J］.声学学报,1991,16(1):19-24. HUIJunying,CAI Ping,MA Xiaomin.Applied study of active notch filter［J］.Acta Acustica,1991,16(1):19-24.

［14］ 常建华,全书海.自适应滤波器的原理、应用及其算法仿真［J］.武汉汽车工业大学学报,1998,20(3):46-49. CHANG Jianhua,QUAN Shuhai.Algorithm,principle and computer simulation of the adaptive filter wave trap［J］.Journal of Wuhan Automotive Polytechnic University,1998,20(3):46 -49.

(编辑:张诗阁)

Adaptive notch filter based active damping controlmethod

WANG Ping, CAIMeng-meng, WANGWei
(Smart Grid Key Laboratory of Education Ministry,Electrical Engineering and Automation Department,Tianjin University,Tianjin 300072,China)

The LCL filter iswidely applied as interface between grid-connected inverter and grid due to a preferable high frequency attenuation characteristic.In the condition of weak grid,impedance value of grid model cannot be ignored,and the existence of grid impedance results in different LCL resonant frequencies,which challenges traditional active damping control.Based on the analysis of band pass filter based active damping control strategy,an adaptive active damping control was proposed by introducing the application of active notch filter,which can adjust the position of negative resonance point adaptively so as tomanage sudden grid changes.Theoretical analysis and simulation results presented on the platform of grid-connected PV inverter system indicate the effectiveness and adaptability of this active damping strategy:deviation of system resonance point is correctly traced,besides,harmonic contents of the resonance point and nearby frequency bands is significantly reduced.In addition,system stability can be ensured by the rapid dynamic response characteristic when there is a voltage leap within±5%.

weak grid;grid-connected inverter;active damping control;self-adaptation control;notch filter

10.15938/j.emc.2015.09.016

TP 13

A

1007-449X(2015)09-0108-09

2014-04-03

高等学校博士学科点专项科研基金(20120032110070)

王 萍(1959—),女,教授,博士生导师,研究方向为电力电子变换术及其控制、智能检测与控制、电子电路与系统;蔡蒙蒙(1990—),女,硕士研究生,研究方向为光伏并网逆变器及其控制;王 尉(1990—),男,硕士研究生,研究方向为电力电子变换技术。

蔡蒙蒙