低开关频率下三电平逆变器的中点电位控制

袁庆庆, 伍小杰, 戴鹏, 夏鲲

(1.上海理工大学光电信息与计算机工程学院,上海200093;2.中国矿业大学信息与电气工程学院,江苏徐州221008)

低开关频率下三电平逆变器的中点电位控制

袁庆庆1, 伍小杰2, 戴鹏2, 夏鲲1

(1.上海理工大学光电信息与计算机工程学院,上海200093;2.中国矿业大学信息与电气工程学院,江苏徐州221008)

为减少大功率变换器功耗,需降低器件开关频率,但将造成输出侧电流谐波含量显著增加,影响三电平逆变器中点电位控制精度。为解决这一问题,以二极管籍位型三电平逆变器为对象,在分析低开关频率对中点电位影响的基础上,明确了三电平逆变器低开关频率分段调制的理论分界点。针对低调制度区域所采用的常规SVPWM算法,提出了一种基于桥臂优化选取的中点电位控制方法,该方法只需判断中点电位差,无需引入输出侧电流,从而避免了低开关频率下电流畸变严重对电流极性的影响,有效保证了中点电位平衡。仿真及实验验证了该中点控制方案在开关频率500 Hz时,仍能保持较好的中点电位误差在1%Vdc之内。

三电平;低开关频率;中点电位;分段调制分界点;桥臂优化选取

0 引 言

三电平逆变器以其输出电流波形平滑、开关器件承压低等优点,广泛应用于大功率传动领域,其中尤以二极管籍位型拓扑使用最广［1-3］,其中点平衡问题是影响其运行性能的重要因素之一［4-5］。为降低大功率变换器功耗,需降低器件开关频率,但其在提高变频器输出能力的同时,造成输出侧电流谐波含量显著增大［6-7］,影响中点电位控制难度［8］。

针对三电平逆变器的中点平衡问题,目前较为常见的一种方法是:通过调节冗余小矢量的作用时间来实现中点电位控制,如平衡因子法、虚拟矢量中点控制等［9-10］;在开关频率较低时,可能存在因电流畸变严重而影响控制效果的问题。另一种方法是根据中点电流方向,注人或抽取零序电压,实现中点电流变向从而完成中点电位控制;但在低开关频率下,中点电流方向提取困难［11］。同时,由于谐波电流在一个开关周期内无法快速衰减至零,在动态调节过程中容易出现中点电位波动叠加,严重时将导致装置无法正常运行。

开关频率较低(＜500Hz)时,常规载波调制、空间矢量调制产生的载波边带将呈现低次谐波特性,影响系统运行,故不适用于大功率场合［12］。目前研究较多的是诸如特定谐波消除法(selective harmonic elimination,SHE)、电流谐波最小法(current harmonic minimum,CHM)等基于开关角直接调制的优化PWM算法［13-14］,此类优化算法能有效改善低开关频率下电流畸变严重的问题,且其属于同步对称调制,中点电位自平衡［15］。由于上述优化PWM算法相对算法复杂、动态性能不佳,文献［12］中提出了结合不同调制度的分段同步调制方式,这也是目前很多大功率传动领域所采样的调制方式,即当调制度大于某一值时采用优化PWM算法,反之采用常规SVPWM算法;但其并未给出明确的分段调制分界点,也未考虑低开关频率下低调制度区的中点电位平衡问题。

文章首先基于二重傅里叶解析的PWM环节谐波组成结果,理论明确了大功率逆变器分段调制的分界点,分析高调制度区域采用优化PWM时的中点电位控制效果。接着在分析输出侧电流对中点电位控制影响的基础上,研究一种适用于低开关频率低调制度区常规SVPWM的中点电位控制方法。该方法无需实时检测输出侧的电流信号,只需通过判断中点电位差来优化选择开关桥臂,从而避免了低开关频率下电流畸变严重的问题。最后,基于仿真及实验验证了该中点控制方法在开关频率低至500 Hz时的中点电位控制效果。

1 分段调制理论分界点

其中:fs为器件开关频率;f为逆变器输出频率。

当逆变器输出频率f降低时,逆变器PWM环节输出的脉冲数N随之增大,此时若仍采用SHEPWM等优化PWM算法,导致开关角求解计算量与实现难度的显著增加［15］;且此时优化PWM与SVPWM相比性能基本类似,故需在一定范围内进行分段调制。

定义调制度M为

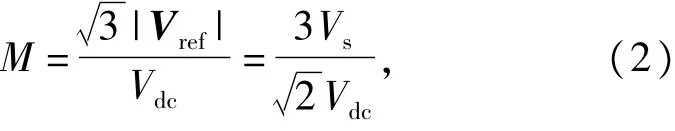
定义一个开关周期内PWM环节的脉冲数N为

其中:Vdc为直流侧电压;Vs为输出侧三相电压幅值; Vref为参考电压矢量幅值;考虑恒功率坐标变换时转

假设逆变器的额定输出电压幅值为Vsn,对应的额定输出频率为fsn,此时对应调制度达到最大值M=≈1.15。逆变器实际输出频率f与额定输

max出频率fsn间存在以下关系

将式(2)代人式(3),可得

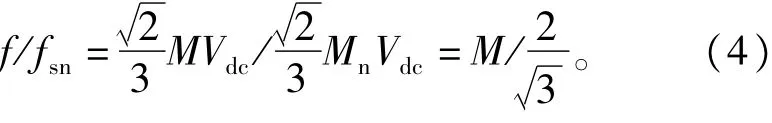
由文献［16］中二重傅里叶解析PWM环节谐波组成结果可知,当一个开关周期内的脉冲数N＜15～20时,由开关频率造成的载波边带会呈现出低次谐波特性,此时应采用优化PWM算法。如以N=15

为例,存在的最低次谐波边带为7次,已呈现低次谐波特性。当N＜15～20时,若考虑fsn=50 Hz,有

考虑目前国内外大功率变频调速中常见的几种器件开关频率方式,文章分别以fs=500 Hz、350 Hz、150 Hz三种情况进行分析:当器件开关频率fs=500Hz时,M＞(0.577～0.770)时,优化PWM算法较为合适;当fs=350 Hz时,M＞(0.404～0.539)时,优化PWM算法较为合适;当fs=150 Hz时,M＞(0.173～0.231)时,优化PWM算法较为合适;为确保低次谐波成分较小,一般取下限。

2 中点平衡问题

在50 kW实验平台上对不同开关频率fs、逆变器输出频率f值时的中点平衡问题进行分析,平台拓扑结构如图1所示。核心控制器为TI公司的高性能浮点DSP TMS320F28335,IGBT的额定电压为1 200 V、额定电流为40 A,两个分压电容为450 V/ 2200μF,直流侧给定电压为690 V。将电容电压和线电流通过SPI协议驱动DAC7724U芯片,最后输出到DPO3014示波器上。

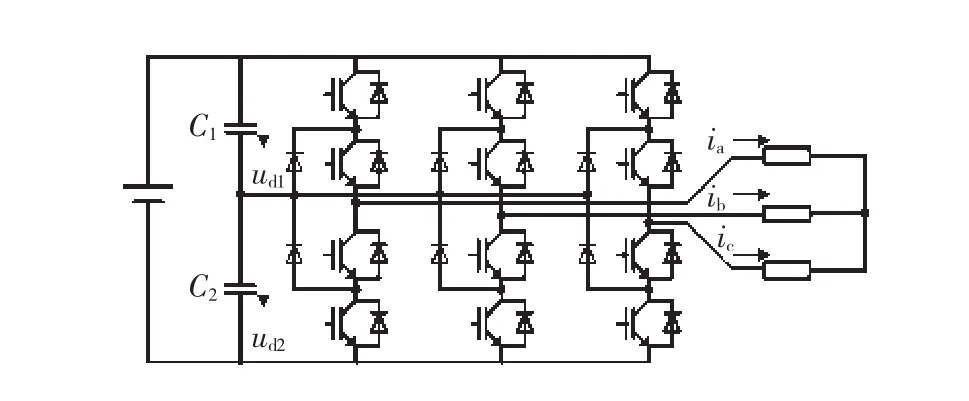
图1 二极管箱位型三电平逆变器拓扑结构Fig.1 Topology of a three-level inverter

当器件开关频率fs=5 kHz、逆变器输出频率f= 50 Hz时,一个开关周期内的脉冲数为100,调制度M为1.15,对应的中点电位及逆变器输出a相电流波形如图2所示。

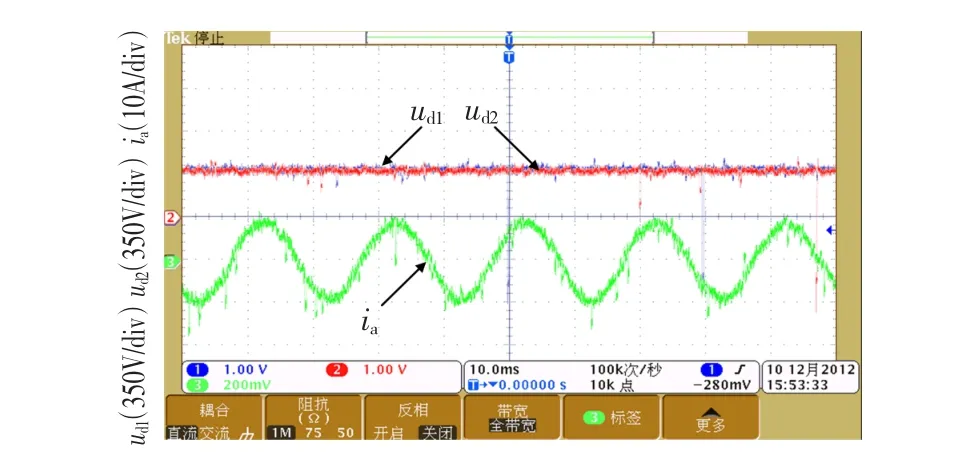
图2 fs=5 kHz,f=50 Hz时的中点电位及线电流波形Fig.2 W aveforms of neutral point potential and line current w ith fs=5 kHz,f=50 Hz

由图2可知,在开关频率较高时,采用常规SVPWM算法能保证输出电流平滑、中点电位平衡。当fs=500 Hz,f=50 Hz时,一个周期内的脉冲数为10、调制度M为1.15,采用SHEPWM优化算法后的中点电位及相电流波形如图3所示。

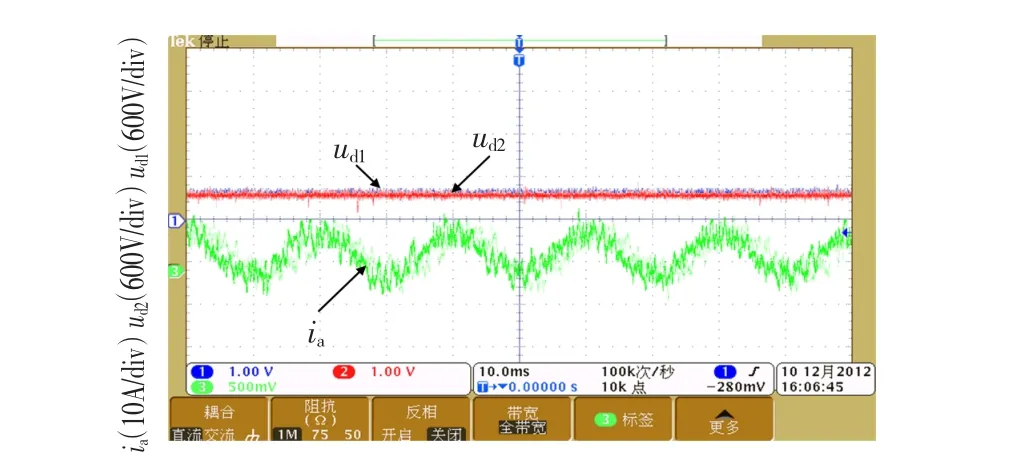
图3 fs=500 Hz,f=50 Hz时的中点电位及线电流波形Fig.3 Waveforms of neutral point potential and line current w ith fs=500 Hz,f=50 Hz

由图3可知,此时虽然输出电流波形不够平滑,但其中点电位是平衡的,这是由于SHEPWM算法的同步对称性造成的。

当fs=500 Hz、f=20 Hz时,一个开关周期内的脉冲数为25、调制度M为0.462,根据上文分段调制分界点的分析,此时采用SVPWM算法更为合适,此时由DPO3014采集得到的中点电位及a相电流波形如图4所示。

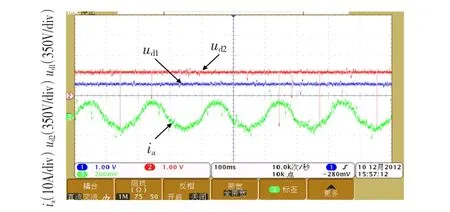
图4 fs=500 Hz,f=20 Hz时的逆变器输出电流波形Fig.4 W aveform of current w ith fs=500 Hz,f=20 Hz

由图4可知,在低开关频率低调制度区域,采用SVPWM会造成逆变器输出侧电流畸变严重、且无法保证中点电位的控制效果。

3 基于桥臂优化选取的中点电位控制

3.1 原理分析

三电平逆变器的开关矢量图如图5所示［7］,fsmax=500 Hz所对应的低调制度区位于阴影区域内,此时,三电平调制运行于内六边形内。

以参考电压矢量在A扇区为例,若仅由上桥臂开关(S+)动作,则开关顺序及对应的作用时间为

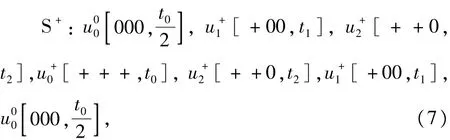
其中,t0+t1+t2=Ts/2,Ts为开关周期。

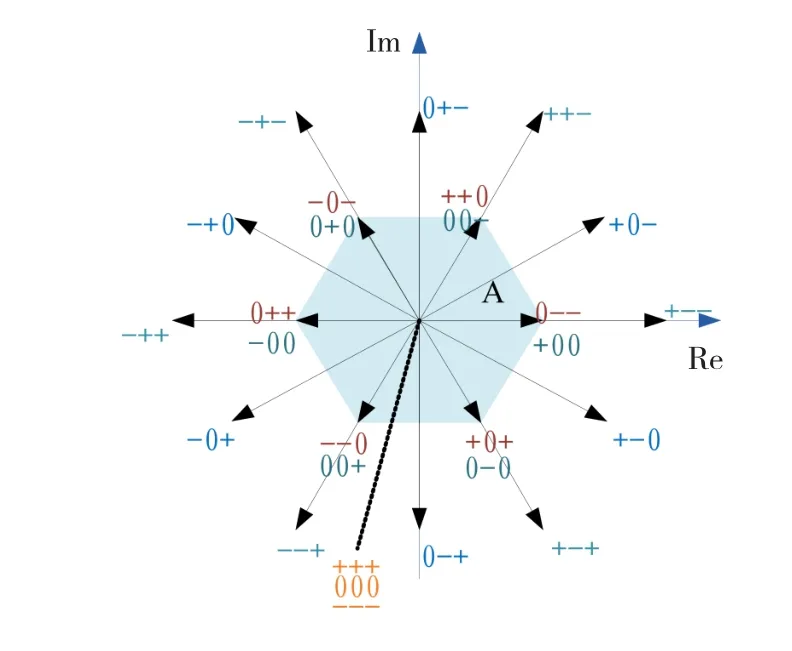
图5 三电平逆变器开关矢量图Fig.5 Sw itch vector diagram of three-level inverter

若仅由下桥臂开关(S-)动作,则开关顺序及对应的作用时间为

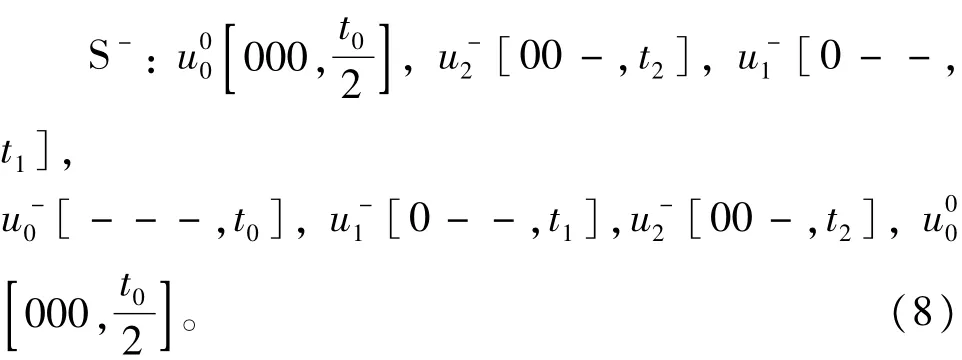
为保证上下桥臂开关动作时脉冲连续性,无论S+还是S-动作,都从u00(000)开始、u0

0(000)结束。

以图1中标注的电流正方向为例,当S+动作时,一个开关周期内流人中点的电流平均值为

由上分析可知,在稳态情况下,若能保持上下桥臂的交替开通与关断,中点电流in能保持稳定,从而实现中点电位平衡。

3.2 低调制度区域的中点电位控制

以图6所示三电平桥臂电路为例,规定中点电流、电压的正方向。令Δun=ud1-ud2,可得如下关系:

1)Δun＞0时,S+动作,中点电流in为负,ud1减小,Δun趋向于零;

2)Δun＜0时,S-动作,中点电流in为正,ud2减小,Δun趋向于零;

3)Δun=0时,S+与S-交替动作,保持中点平衡。

通过以上工作,可将中点电流in的实时检测工作转换成对中点电位差Δun=ud1-ud2正负值的实时检测,这样就可避免因开关频率降低而导致的输出电流谐波畸变对检测精度的影响。

图6 中点电流、电压的正方向Fig.6 Positive direction of the neutral point potential and current

实际运行中,中点电位允许一定范围内的偏差,故引人中点电位偏差的阈值X,当Δun＞X时,S+动作;当Δun＜-X时,S-动作;当-X≤Δun≤X时,S+与S-交替动作。其中,阈值X的取值根据系统控制要求而定,一般取(1%～5%)Vdc。低开关频率下全调制区域的中点电位闭环控制框图如图7所示。

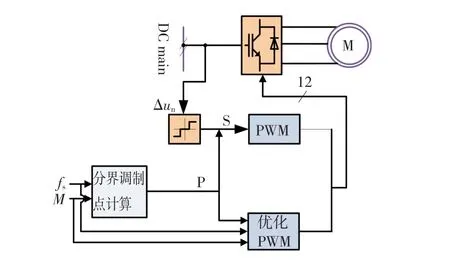
图7 低开关频率下全调制度区域的中点电位控制框图Fig.7 Diagram of the control system for the neutral point potentialw ith low sw itching frequency

由图7所知,本文所设计的低开关频率下的中点电位控制分为以下几部分:1)首先基于实际的器件开关频率fs和调制度M值进行分界调制点计算,生成算法选择信号P,当P为+时,选取常规SVPWM算法;当P为-时,选取优化PWM算法。2)低调制度区SVPWM的中点电位控制,通过计算中点电位差,然后经过阈值判断环节产生桥臂优化选择的指令信号S,当S＞0时,仅限上桥臂动作;当S＜0时,仅限下桥臂动作;当S=0时,上下桥臂交替动作。

4 仿真与实验验证

4.1 仿真分析

为验证本文所提出中点电位控制方案的可行性,首先针对高调制度区域采用SHEPWM时中点电位控制进行仿真验证。如图8所示为对1 600 kW电励磁同步电机进行低开关频率下SHEPWM调制时的中点电位波形,其中直流侧电压vdc的给定值为1 000 V,并在t=7.5 s时进行电机负载突变。

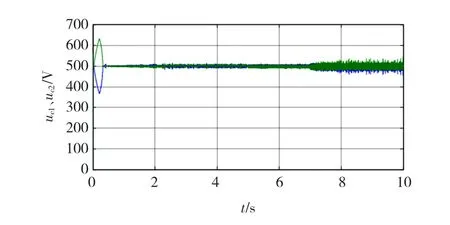
图8 1 600 kW电机SHEPWM调制时的中点电位波形Fig.8 Neutral point potential for 1 600 kW EESM at low sw itching frequency w ith SHEPWM

由图8可知,优化PWM调制算法因其自身的中点自平衡特性,能在较低开关频率下保持良好的中点电位控制效果。图9为fs=500 Hz、f=20 Hz,采用SVPWM算法时的中点电位控制仿真波形,其中直流侧电压Vdc的给定值为200 V,图9(a)为常规中点控制时的波形,图9(b)为采用本文所研究的桥臂优化选取时的中点电位控制效果。

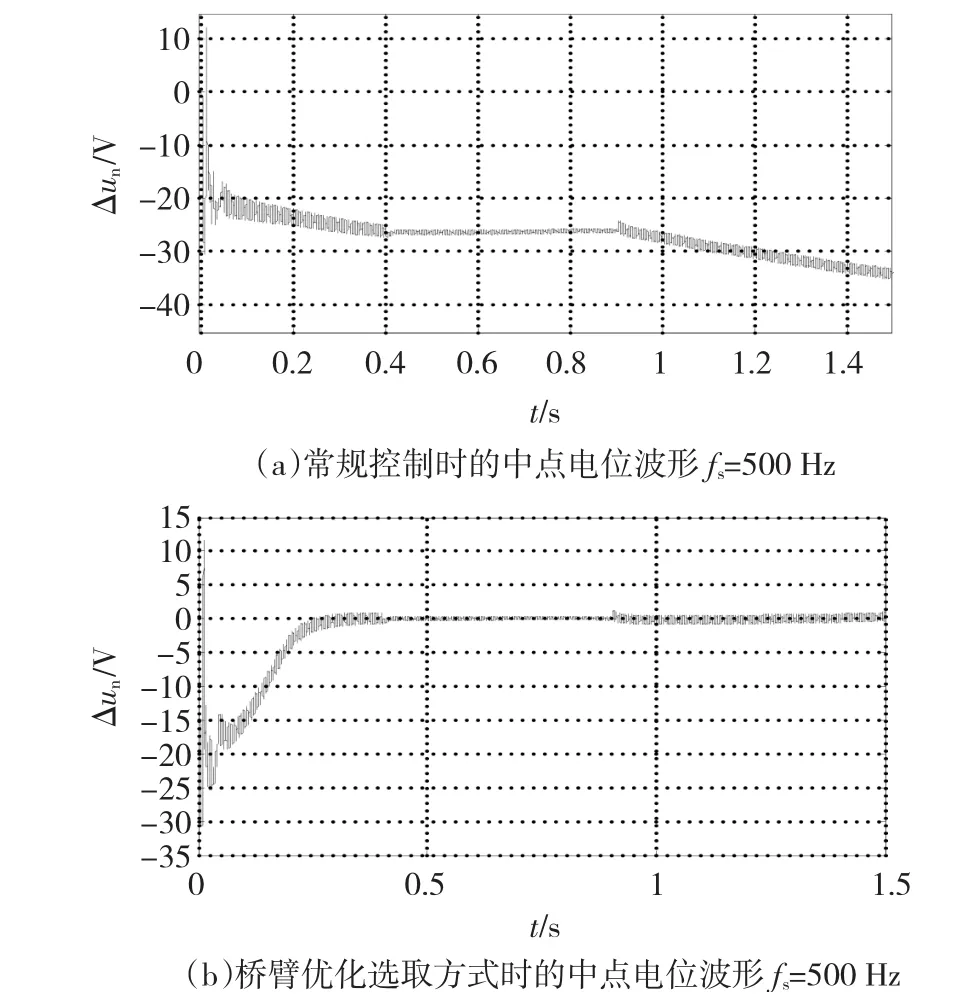
图9 低开关频率低调制区域的中点电位仿真波形Fig.9 Neutral point potential waveforms w ith a low sw itching frequency and a low index M

由图9(a)可知,当在低开关频率、低调制度区域采用常规方式进行中点电位控制时,中点电位差最大会超过15%Vdc;本文采用的桥臂优化选取控制方式能实现fs=500 Hz、f=20 Hz条件下,中点电位差保持在1%Vdc内,验证了本文研究方案的可行性。

4.2 实验验证

基于TMS320F28335搭建了50 kW三电平逆变器带阻感负载的实验平台。直流侧电容C1=C2= 2 200μF,直流侧电压Vdc=690 V,器件IGBT的开关频率为fs=500 Hz,输出侧频率为f=20 Hz,对应调制度为M=0.462。采用本文研究的基于桥臂优化选取的中点电位控制方案时,实验过程中阈值X设定为1%Vdc,此时的中点电位波形(由控制-不控-控制)如图10所示。

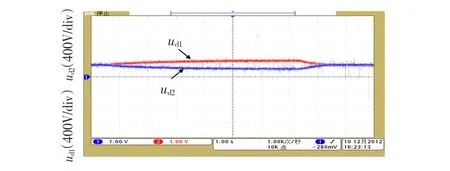
图10 fs=500 Hz,M=0.462时的中点电位实验波形Fig.10 W aveforms of neutral point potential w ithfs=500 Hz,M=0.462

由图10可知,在器件开关频率较低、调制度较低情况下,采用常规中点控制方法时,电容电位差较大,影响装置正常工作。当加人本文所提出的基于桥臂优化选择的中点电位控制策略时,中点电位能保持平衡,电容电位差为1%Vdc。此时逆变器输出的a相电流波形及对应的中点电位波形如图11所示;图12则为直流侧电压给定由690 V突变至900 V时对应的中点电位及此时的a相电流波形。

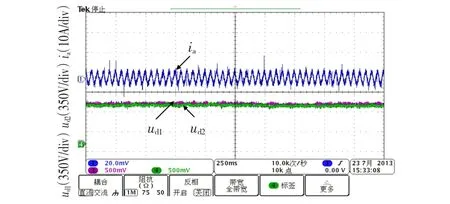
图11 fs=500 Hz时的输出侧a相电流波形及中点电位Fig.11 Output current and the neutral point potential waveforms w ith fs=500 Hz

由图12可知,当直流侧电压Vdc给定突变时,本文研究的基于桥臂优化选取方式仍能实现良好的中点电位控制效果。

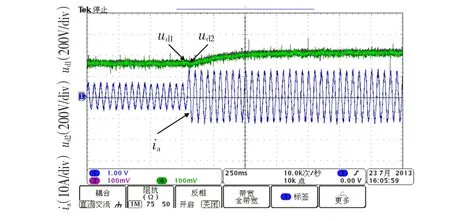
图12 直流侧电压给定突增时的a相电流波形及中点电位Fig.12 Output current and the neutral point potential waveformsw ith an enlargement of Vdc

5 结 论

低开关频率下的大功率三电平逆变器常采用分段调制策略,在高调制度区采用中点自平衡的同步优化PWM算法;在低调制度区采用常规SVPWM算法。本文首先基于二重傅里叶解析结果从理论角度明确了此类分段调制的分界点。接着,研究了一种桥臂优化选取的新型中点电位控制方式,能有效避免低开关频率下电流畸变严重对中点电位控制精度的影响,维持中点电位差在1%Vdc内,并通过仿真及实验得到了验证。同时,由于本文是基于低开关频率下分段调制算法的前提研究的,故需考虑实际系统中分段调制的切换问题及其他一些诸如非线性等的影响,这也是本文的后续工作。

［1］ 张志,谢运祥,乐江源,等.二极管钳位型单相三电平逆变器空间矢量脉宽调制方法［J］.中国电机工程学报,2010,30 (27):62-68. ZHANG Zhi,XIE Yunxiang,LE Jiangyuan,et al.Study of SVPWM method for single-phase three-level diode-clamped inverter［J］.Proceedings of the CSEE,2010,30(27):62-68.

［2］ 洪峰,稽保健,杨伟,等.二极管钳位型双Buck三电平逆变器输人均压解藕控制［J］.中国电机工程学报,2012,32(9): 34-40. HONG Feng,JIBaojian,YANGWei,etal.Decoupling control of input voltage balance for diode-clamped dual buck three-level inverters［J］.Proceedings of the CSEE,2012,32(9):34-40.

［3］ 周京华,贾斌,章小卫,等.三电平逆变器死区补偿策略研究［J］.电机与控制学报,2013,17(5):69-74. ZHOU Jinghua,JIA Bin,ZHANG Xiaowei,et al.Research on dead-time compensation strategy of three-level inverter［J］.Electrical Machines and Control,2013,17(5):69-74.

［4］ 范必双,谭冠政,樊绍胜.三电平双PWM变换器电容电压平衡综合控制［J］.电机与控制学报,2014,18(1):38-43. FAN Bishuang,TAN Guanzheng,FAN Shaosheng.Integrated control of capacitance voltage balancing for back-to-back three-level PWM converters［J］.Electrical Machines and Control,2014, 18(1):38-43.

［5］ 姜卫东,王群京,陈权,等.考虑中点电压不平衡的中点籍位型三电平逆变器空间矢量调制方法［J］.中国电机工程学报,2008,28(30):20-26. JIANGWeidong,WANG Qunjing,CHEN Quan,et al.SVPWM algorithm for NPC three-level VSI considering unbalance neutral point voltage［J］.Proceedings of the CSEE,2008,28(30):20 -26.

［6］ YUAN Qingqing,WU Xiaojie,DAIPeng,et al.Control of electrically excited synchronousmotors with a low switching frequency［J］.Journal of Power Electronics,2012,12(4):615-622.

［7］ HOLTZ J,OIKONOMOU N.Estimation of the fundamental current in low-switching-frequency high dynamic medium-voltage drives［J］.IEEE Transactions on Industrial Application,2008,44(5):1597-1605.

［8］ HOLTZ J,OIKONOMOU N.Neutral point potential balancing algorithm at low modulation index for three-level inverter mediumvoltage drives［J］.IEEE Transactions on Industrial Applications,2007,43(3):761-768.

［9］ POU J,PINDADO R,BOROYEVICH D.Evaluation of the lowfrequency neutral-point voltage oscillations in the three-level inverter［J］.IEEE Transactions on Industrial Electronics,2005,52 (6):1582-1588.

［10］ BUSQUETS-MONGE S,BORDONAU J,BOROYEVICH D,et al.The nearest three virtual space vector PWM-amodulation for the comprehensive neutral-pointbalancing in the three-level NPC inverter［J］.Power Electronics Letters,2004,2(1):11-15.

［11］ STEINKE J K.Switching frequency optima PWM control of a three-level inverter［J］.IEEE Transactions on Power Electronics,1992,7(3):487-492.

［12］ 符晓.电励磁同步电机低开关频率控制技术研究［D］.徐州:中国矿业大学,2011.

［13］ 张永昌,赵争鸣,张颖超,等.三电平变频调速系统SVPWM和SHEPWM混合调制方法的研究［J］.中国电机工程学报,2007,27(16):72-77. ZHANG Yongchang,ZHAO Zhengming,ZHANG Yingchao,et al.Study on a hybrid method of SVPWM and SHEPWM applied to three-level adjustable speed drive system［J］.Proceedings of the CSEE,2007,27(16):72-77.

［14］ WANG Chenchen,LIYongdong.Analysis and calculation of zero-sequence voltage considering neutral-point potential balancing in three-level NPC converters［J］.IEEE Transactions on Industrial Electronics,2010,57(7):2262-2271.

［15］ DU TOITMOUTON H.Natural balancing of three-level neutralpoint-clamped PWM inverters［J］.IEEE Transactions on Industrial Electronics,2002,49(5):1017-1025.

［16］ HOLMES D G,LIPO T A.Pulse width modulation for power converters:principles and practice［M］.New York:Wiley Publishing,2003:110-180.

(编辑:张诗阁)

Neutral point potential control for three-level inverters w ith low sw itching frequency

YUAN Qing-qing1, WU Xiao-jie2, DAIPeng2, XIA Kun1
(1.School of Optical-Electrical and Computer Engineering,University of Shanghai for Science and Technology,Shanghai200093,China;2.School of Information and Electrical Engineering,China University of Mining and Technology,Xuzhou 221008,China)

The switching frequency of the three-level inverters is usually kept low to reduce the dynamic losses of the high-power inverters and which results in an increase in the harmonic components of the output current,and affects the control difficulties of the neutral point potential.According to these problems,the influence on the neutral point potential by the output currentwas analyzed,aswell as the first proposing of the demarcation point for the subsection modulation.For low modulation index,the normal pulse width modulation would bemore appropriate.A novel approach controlling the neutral point potential for the low modulation index was proposed based on the optimal selection of the sub-bridges.This new method doesn'tneed the output currentas a feedback signal,which avoids the affect from the severe distortion of the output current at low switching frequency.Experimental results verify thatmethod can maintain the neutral point potential balancing with the switching frequency as low as 500Hz.

three-level;low switching frequency;neutral point potential;demarcation point of subsection modulation; optimal selection of sub-bridges

10.15938/j.emc.2015.09.009

TM 464

A

1007-449X(2015)09-0061-06

2013-05-31

国家自然科学基金项目(51077124,51207091);沪江基金(B14002/D14002)

袁庆庆(1987—),女,博士,讲师,研究方向为大功率变频调速和新能源发电等;伍小杰(1966—),男,博士,教授,研究方向为电力电子传动与电机控制保护等;戴 鹏(1973—),男,博士,教授,研究方向为大功率传动技术和多电平技术等;夏 鲲(1980—),男,博士,副教授,研究方向为无刷电机控制和新能源发电等。

袁庆庆