三相4线制有源电力滤波器滑模变结构控制

谢丰，何怡刚，王东楼，张金安

（合肥工业大学电气与自动化工程学院，安徽合肥230009）

1 引言

近年来，大量的非线性负载投入到电网中去，从而使得电力系统电压、电流波形发生畸变。有源电力滤波器（APF）作为一项动态抑制谐波和无功的措施得到了广泛的研究和应用，但大量相关研究仅限于三相3 线制，而我国的实际情况是低压用户大都采用三相4线制。三相4线制有源电力滤波器不仅要滤除三相谐波，还要滤除中线电流，使得中线电流接近零。

在传统的谐波抑制策略中，有滞环控制方法、三角载波控制方法等［1］。滞环控制方法具有硬件电路简单、电流响应快等特点，但其开关频率不固定，当滞环宽度较大时，开关频率较低但跟踪效果不理想，若环宽较小则会使得器件的开关频率过高而导致器件损坏；三角载波控制方法具有开关频率固定的优点，但其硬件电路相对复杂，且跟踪误差较大。

滑模控制［2］方法又称变结构控制，其最大的优点在于它的鲁棒性。此外，动态响应快也是滑模变结构控制的另一大优点。国内外学者自上个世纪80年代以来就进行了大量的研究，已发表了大量的学术论文［3-5］。其中大多数都是将滑模控制技术应用在三相3线制有源电力滤波器和单相有源电力滤波器中，并取得了良好的控制效果，而其在三相4 线制有源电力滤波器中的应用相对较少。

本文在前人研究的基础之上，将三维空间矢量概念与滑模变结构控制技术相结合，提出了一种可应用于三相4 线制系统的新型APF 控制方案，所提控制策略不仅可以滤除三相谐波电流，还可以将中线电流抑制在极小的范围之内，使得输出三相电源电流波形为近似正弦，达到预期的控制目标。

2 三相4 线制有源电力滤波器拓扑结构

电压型三相4线制有源电力滤波器有3桥臂和4桥臂两种类型。其中4桥臂变流器不需要进行中点钳位控制，且拥有较好的直流侧电压利用率、直流侧电容相对较小，是目前的一个研究热点［6］。因此，本文采用三相4桥臂变流器，其拓扑结构如图1所示。

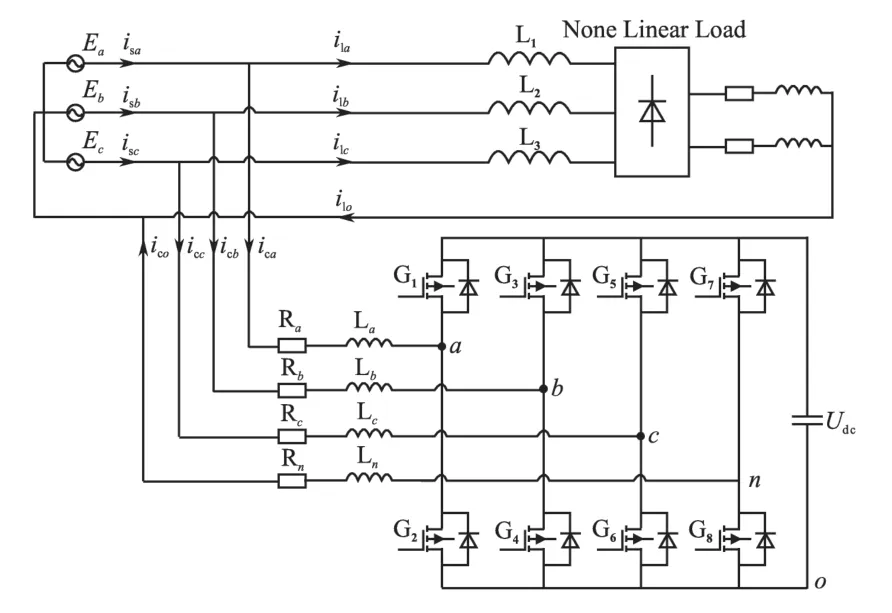
图1 三相4线制4桥臂APF拓扑结构Fig.1 Structure of three phase four wire active power filter

其中，非线性负载采用二极管不控整流电路，电力电子器件选择MOSFET，Rx（x=a，b，c），Lx为交流侧电阻和电感，L1，L2，L3为平波电感，Rn，Ln为中线电阻和电感。

3 谐波检测环节和直流侧电压控制

本文采用瞬时无功功率理论进行谐波检测，对应的控制框图如图2所示。

为了使直流侧电压保持恒定，将Udc的给定值与测量值相减，再经过PI 调节，得到调节信号Δip，把它叠加到瞬时有功功率的直流分量上去，这样指令电流中包含一定的基波有功分量，从而使得有源电力滤波器的直流侧与交流侧交换能量，将直流侧电容电压调节到给定值。

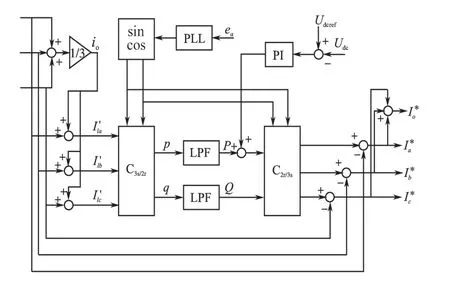
图2 三相4线制APF谐波检测及直流侧电压控制Fig.2 Harmonic current detection and DC voltage control

4 三相4 桥臂有源电力滤波器数学模型

在分析APF的控制方法之前，有必要建立其数学模型，其中包括静止abc 坐标系模型和旋转dq0坐标系模型。

4.1 静止abc坐标系下的数学模型

由图1 可得三相4 线制4 桥臂有源电力滤波器在abc坐标系下的数学模型为

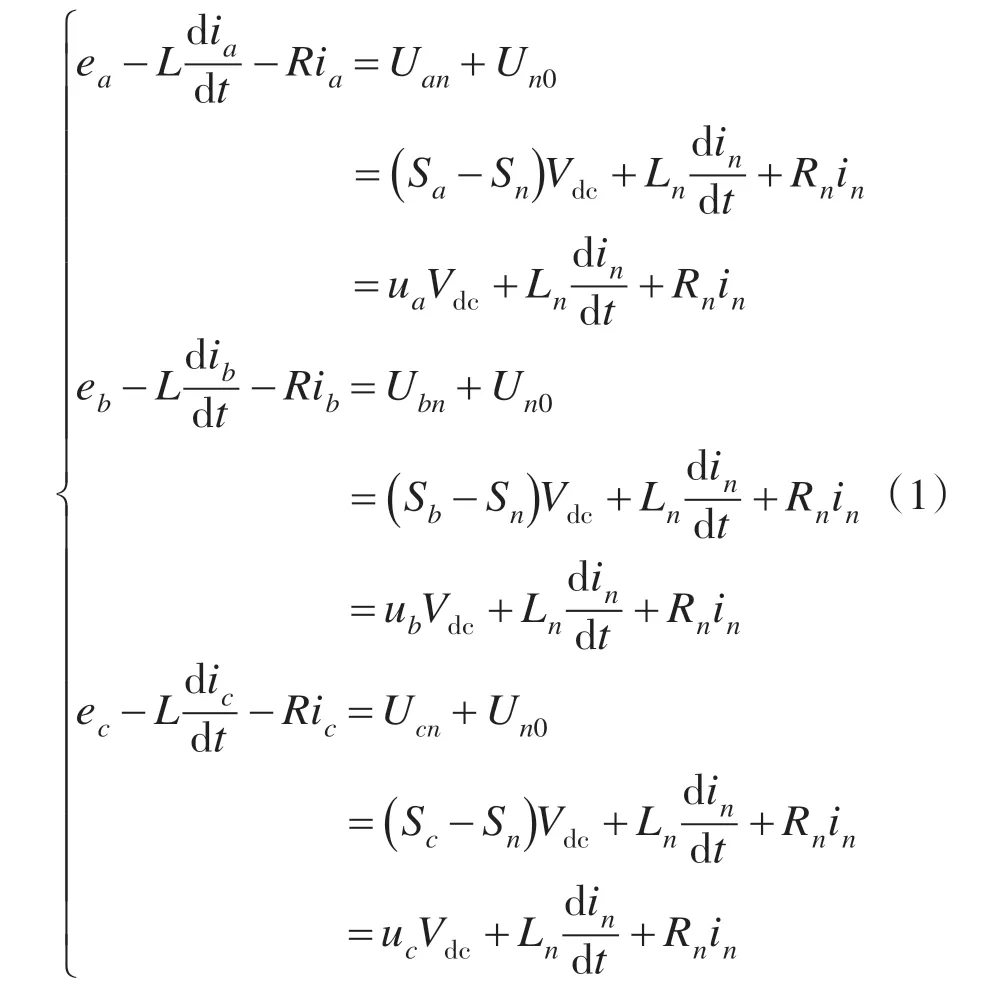
式中：Sx（x=a，b，c）为开关函数，当上桥臂导通下桥臂关断时，S=1，反之S=0；为简化，设Ln=L，Rn=R。

4.2 三维静止电压矢量图［7］

4桥臂逆变器上的三维空间矢量实际上是由二维空间矢量拓展得到的。由三相静止abc坐标系转换到三相静止αβγ空间坐标系的逆变器输出电压的变换公式为

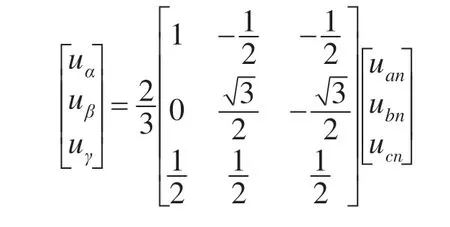
其中 uxn=Sa-Snx=a，b，c

由此得到三相4 桥臂逆变器的三维空间矢量图，如图3所示。

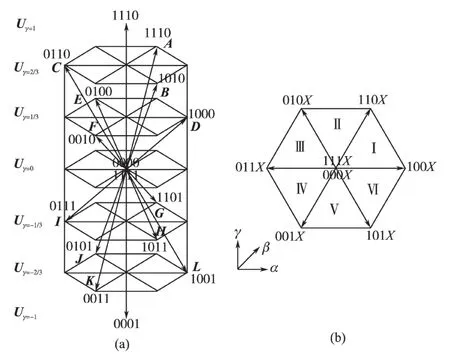
图3 三相4桥臂逆变器空间矢量图及其在αβ坐标系投影Fig.3 Space vector of three phase four leg inventer and its projection inαβcoordinate system

由图3 可以看出，共有16 种开关状态，对应16 个空间矢量。将三维空间矢量图投影到二维平面坐标系中，得到图3b。可以看出，16 个空间矢量投影到αβ系只有7个点，包括6个矢量和2个非零矢量，其中X 表示第4 桥臂的两种开关状态。可以认为三维空间矢量调制是在传统二维矢量调制的基础上，通过第4 桥臂引入γ轴得到的，而二位空间矢量调制可以看成三维空间矢量调制的一个特例。

4.3 dq0坐标系下的数学模型

将式（1）中abc 坐标系中的量通过坐标变换变为dq0 旋转坐标系中的量，由此得到了三相4线制APF 在dq0 旋转坐标系中的数学模型：

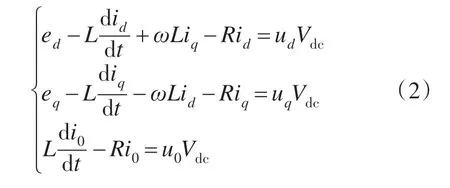
5 滑模控制方法

定义滑模函数Sd，Sq，S0：

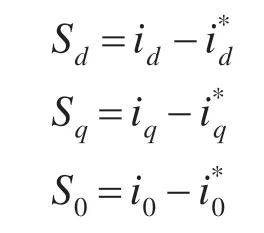
控制输入ud，uq必须依据滑模可达性条件［1］，即：

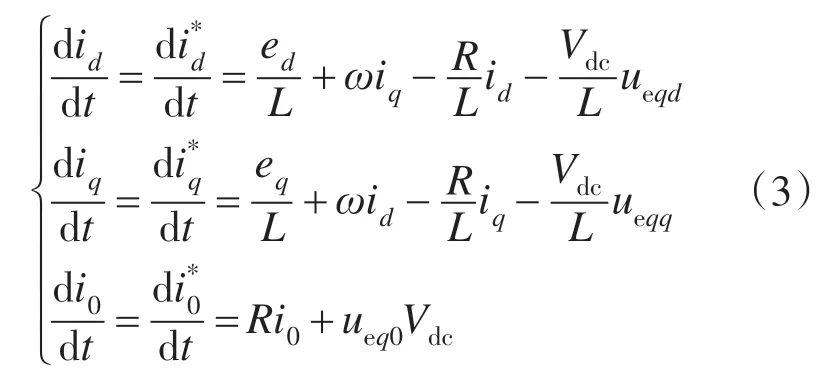
式（2）减式（3）得到：

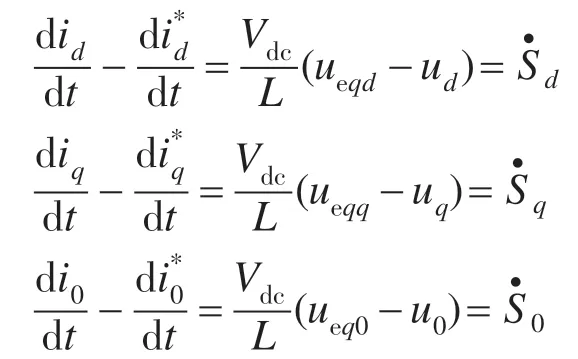
依据可达性条件可得到控制条件为

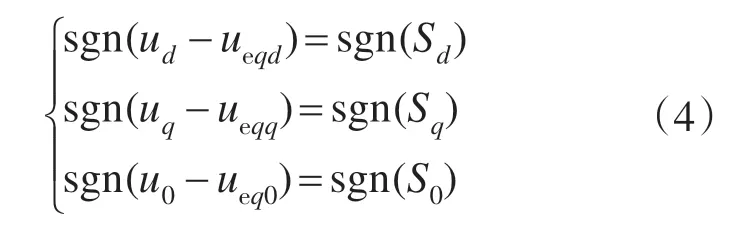
三相4 线制4 桥臂APF 有16 条电压向量，电流环滑模控制器设计的任务就是从这16 条向量中选择出满足可达性条件式（4）的控制电压矢量。以Ueqd，Ueqq，Ueq0均为正且Sd>0，Sq>0，S0>0为例，分析矢量选择过程，如图4所示。

当把矢量图投影到平面时，将（d，q）坐标系沿Ueq的方向平移至Ueq的终点得到（d′q′）坐标系。因Sd>0，Sq>0，则当Ψ∈［-λ，2π/3-γ］时，矢量110坐落在坐标系（d′，q′）的第1象限，即Ud-Ueqd>0，Uq-Ueqq>0，满足可达性条件式（4），此时控制输入应选择110。当矢量图扩展到空间时，增加了一个维度，将原（d′，q′）坐标系垂直向上平移Ueq0个长度单位，得到（d″，q″，0″）坐标系，当Sd>0，Sq>0，S0>0，且Ψ∈［-λ，2π/3-γ］时，原矢量110的正上方的空间矢量A（1100）落在（d″，q″，0″）坐标系的第1 象限，即有Ud-Ueqd>0，Uq-Ueqq>0，U0-Ueq0>0，满足可达性条件式（4）。其中，Ψ为d 轴与α轴之间的夹角。定义

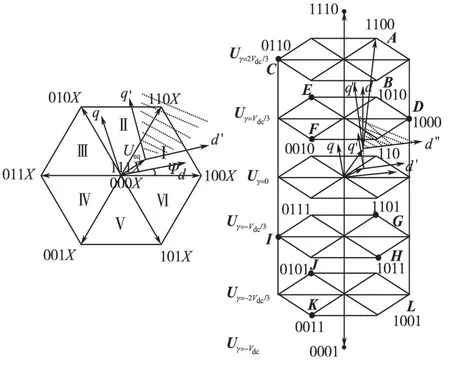
图4 控制电压矢量及其选择Fig.4 Control voltage vector and its selection

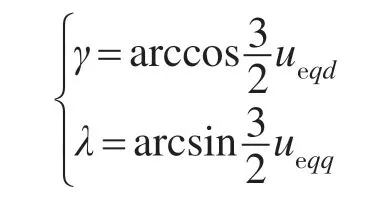
依然以ueqd，ueqq均为正且Sd>0，Sq>0 为例，角度λ的意义为：将三维空间矢量投影到平面，当（d′，q′）坐标系中的d′轴经过矢量100 时d 轴与α轴的夹角，此时开始选择矢量110（若为三维空间即开始使用矢量A 或者G）；角度γ的意义为：当（d′，q′）中的q′轴经过矢量010时，d轴与α轴的夹角为2π/3-γ，此时结束使用矢量110（空间矢量为A或G）。经过进一步分析，得到空间矢量的选择表，如表1所示。

表1 基于滑模控制的控制矢量选择Tab.1 Control vector selection based on SMC

对表1研究发现，随着等效控制Ueqd，Ueqq的变化，参数λ，γ随之变化，从而造成表1 中Ψ的划分区间发生变化，当π/3-λ+γ>0 时，2 个相邻区间有重叠；而当π/3-λ+γ<0 时2 个相邻区域不连续，这样就造成了控制信号紊乱，影响电流环的动态特性。为了克服上述不足，对表1进行修正，将表1中前一个区间的右区间和后一个区间的左区间相加取平均数，作为新的区间值，由此得到了表2，其中k=（λ+γ）/2。

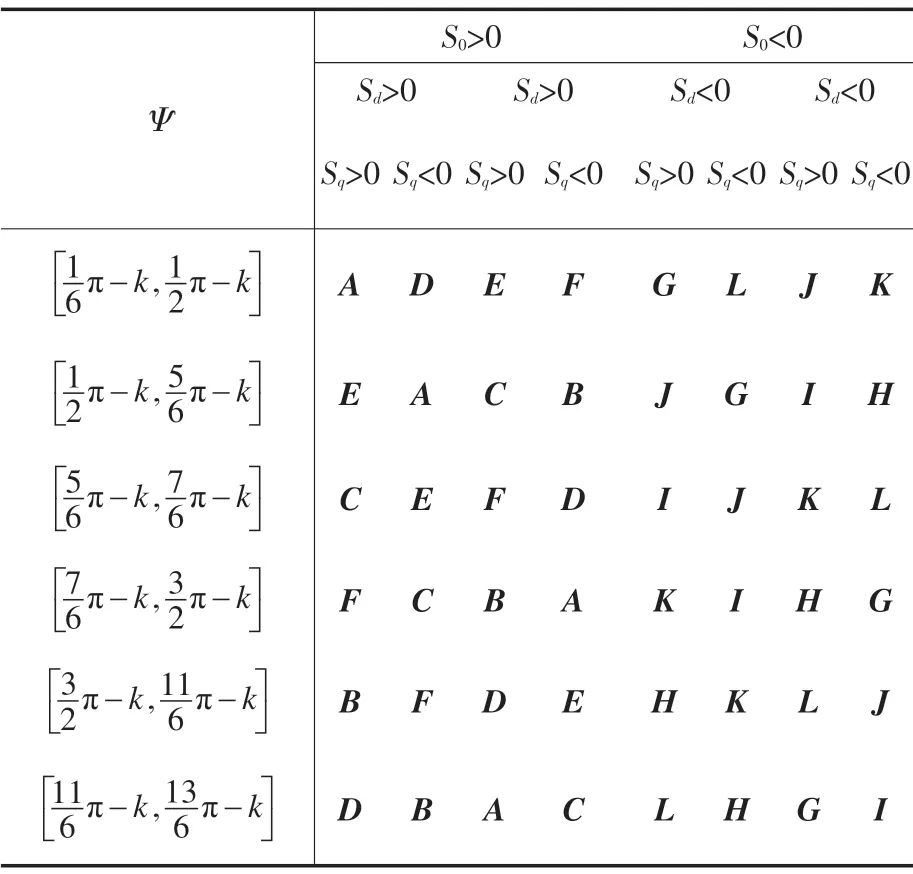
表2 修正后的的控制矢量选择Tab.2 The adjusted control vector selection

6 仿真结果

为实现本文提出的新型控制策略，硬件部分可采用三相整流阻感负载，电流电压信号通过霍耳传感器检测并传送给控制单元（即软件部分），控制单元的核心是DSP 软件，将本文所提出的控制策略编好程序输入到DSP 软件中，DSP 软件根据程序输出相应的控制信号后传送给驱动电路，从而控制电力电子器件的导通与关闭。利用Matlab/Simulink 软件进行仿真分析。系统参数为：电源电压220/380 V，交流侧电感3 mH，交流侧电阻0.3 Ω，直流侧电容2 000 μF，直流给定电压800 V，平波电感3 mH，PI参数Kp=0.2，Ki=0.2。

A 相负载电流波形如图5 所示，可以看出其中含有大量的高次谐波，且有一定的直流分量，没有达到控制要求。

接入有源电力滤波器之后，系统电源电流如图6所示，可以看出，滑模控制使得电源电流已经变为非常好的正弦波形。

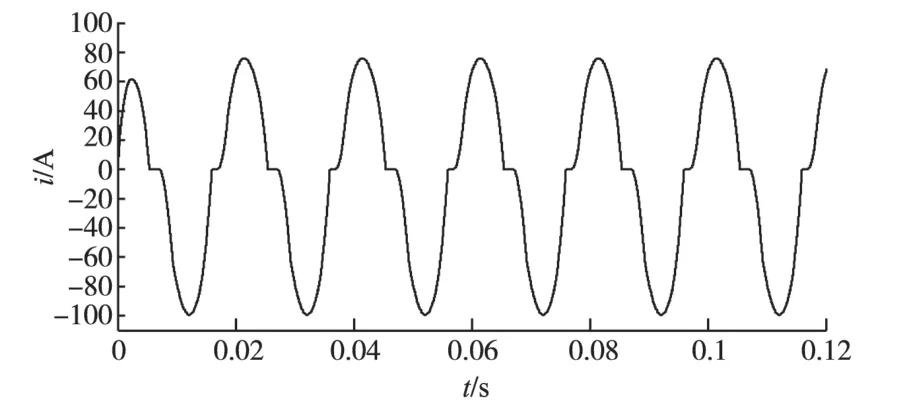
图5 A相负载电流Fig.5 A phase load current

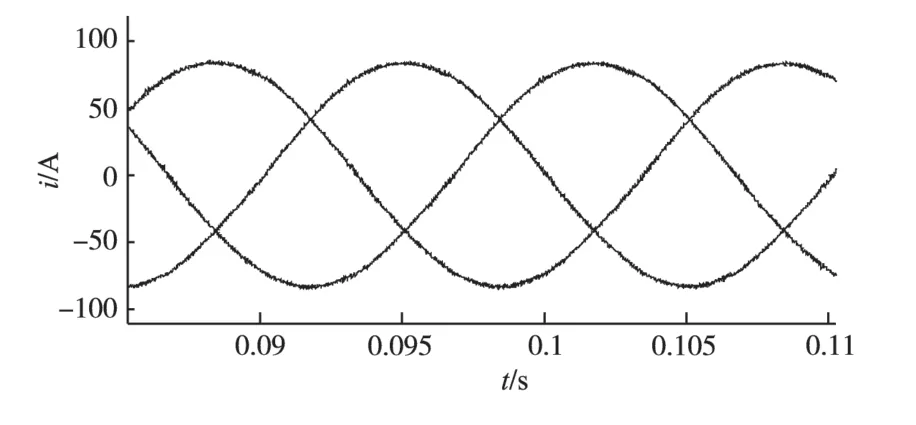
图6 补偿后电源电流Fig.6 Source current after compensation

图7 给出了传统滞环控制下的电源电流波形，可以看出，虽然在整体上滤除了谐波，但其电流波形中含有较大的毛刺，控制效果并不理想。而从图6的波形上看，波形较为平滑，几乎不存在毛刺现象，控制效果较为理想。因此本文提出的方法有很大的优越性。

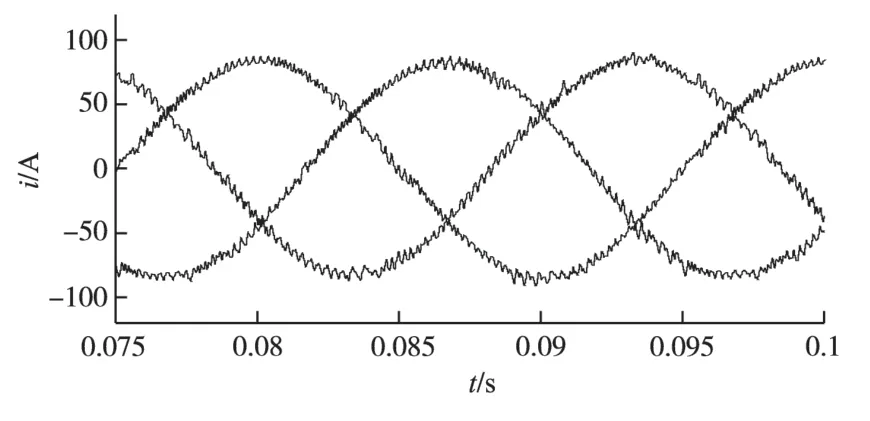
图7 传统滞环控制电源电流Fig.7 Source current with traditional hysteresis control

图8 给出了补偿之后的中线电流波形，由图8可知，经过很短的一段时间，中线电流即被抑制在极小的范围之内，近似为0，达到了系统要求。

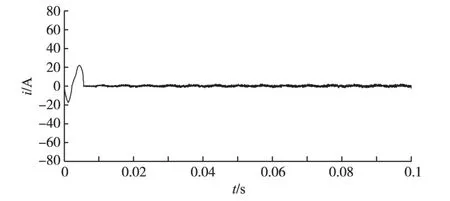
图8 补偿后中线电流Fig.8 Current in middle wire after compensation

图9 给出了直流侧电压的波形，仿真给定值设定为800 V，可以看出直流侧电容电压值很快达到了给定值，并且之后几乎保持了不变，完全满足了控制系统的要求。

图9 直流侧电压波形Fig.9 Wave of DC voltage

7 结论

本文将三维空间矢量概念与滑模变结构控制技术相结合，提出了一种应用于三相4 线制4桥臂的新型控制策略。采用基于瞬时无功功率理论的方法来检测谐波电流并稳定直流侧电压。电流环控制部分，首先建立了APF 在dq0 坐标系中的数学模型，然后通过等效控制的方法得出了控制矢量的选择规则。

仿真结果表明，本文所提的控制策略可以很好地抑制电网谐波，并将中线电流控制在了极小的范围之内。

［1］王兆安，杨君，刘进军，等.谐波抑制和无功功率补偿［M］.北京：机械工业出版社，2005.

［2］张兴，张崇巍.PWM整流器及其控制［M］.北京：机械工业出版社，2012.

［3］鞠建永.基于滑模控制的并联型有源电力滤波器［D］.合肥：合肥工业大学，2002.

［4］Somayeh Yarahmadi，Gholamreza Arab Markade，Jafar Soltani.Current Harmonics Reduction of Non-linear Load by Using Active Power Filter Based on Improved Sliding Mode Control［C］//PEDS TC2013，2013：524-528.

［5］Pempeo Marino，Froncesc Vasca.Sliding Mode Control for Three Phase Rectifier［C］//IEEE PESC1995，1995：1033-1039.

［6］张擎.基于四桥臂逆变器的有源电力滤波器控制策略的研究［D］.合肥：合肥工业大学，2010.

［7］张兴.高等电力电子技术［M］.北京：机械工业出版社，2011.