不对称电网故障下的正序电压分量补偿法

王晓兰，鲜龙，包广清，张晓英，马呈霞

（1.兰州理工大学电气工程与信息工程学院，甘肃兰州730050；2.甘肃电力科学研究院，甘肃兰州730050）

1 引言

双馈风力发电机（DFIG）由于其变流器容量小、造价相对较低、且可以很好地实现变速恒频运行，成为风力发电中的主流机型［1］。但是因其定子绕组直接与电网相连、励磁变流器容量小，导致其抗电网扰动的能力薄弱。电网发生故障时，双馈机组内会产生过电流、过电压，同时会出现转矩暂态冲击、输出有功与无功功率波动等问题，严重地影响了双馈风力发电机组的安全运行和输出电能质量［2-3］。

为了保证双馈风力发电系统的安全可靠运行，行业规程要求，在电网故障期间，并网的风力发电机组能够对电网提供有效支持，即要求并网的风力发电机组具备低电压穿越（LVRT）能力［4-5］。因此，如何进一步提高双馈发电机组的低电压穿越能力，以满足日趋严格的电网规程要求，是风力发电中必须研究的问题［6］。国内外的专家学者从不同的角度出发，提出了各种措施以提高双馈发电机组的低电压穿越能力［7-14］。

目前大部分的研究报道，主要集中于电网出现对称故障的情况。实际上，电网出现不对称故障的几率要比出现对称故障的几率高很多，分析和研究不对称电网故障情况下的低电压穿越技术，更具有实际意义。

文献［15-16］采用了正负序分解、双d-q轴解耦、双PI电流调节器控制的方式。这种基于双PI电流内环的控制方式，能在电网电压不平衡条件下，实现DFIG运行的有效控制，但是在工程实现中，这种方法存在正、负序PI 调节器的参数配合问题。文献［17-18］在电流控制环中引入谐振控制器，构成比例-谐振或比例-积分-谐振控制器，来代替传统的PI调节器。无需转子电流的正、负序分解，仅使用一个控制器来实现对正、负序电流的同时控制，在不对称电网故障下，获得了很好的动、静态性能。但是该控制策略中的一些具体问题还有待于进一步深化研究。文献［19-20］则提出了直接功率控制策略，具有简单、动态响应快、对电机参数依赖小、鲁棒性好等优点，但实现比较复杂。

本文针对双馈风力发电系统中的不对称电网电压故障，基于正负序分解的思想，提出了一种正序电压分量补偿法，将不对称故障问题转化为对称故障处理，简化了控制系统。为了实现正序电压分量补偿方法，在网侧变流器GSC的直流侧接入了由DC-DC 变换器控制的超级电容器，研究了新的拓扑结构中，网侧变流器GSC 的控制策略以及DC-DC 变换器的控制策略。确定了正序电压的参考值的计算方法。采用Matlab/Simulink 构建了相应的仿真模型，验证了该方法的正确性。研究结果表明，采用本文的方法，在电网电压跌落80%的情况下，可以将故障相的电压迅速地恢复至正常值的80%以上，同时保证非故障相电压不超过正常值的120%。

2 不对称故障分析

假设电网在某一时刻发生了不对称故障为单相电压跌落，以使后续的分析直观明了。并以A 相为故障相，其电压值跌落至正常电压值的k倍，即故障后的三相电网电压为

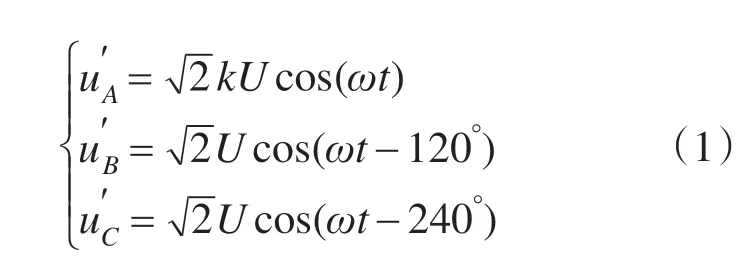
按照对称分量法得到相应的正序分量电压与负序分量电压，即

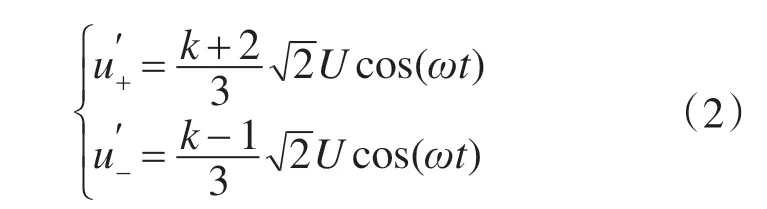
很显然，正序电压的幅值是负序电压幅值的(k+2)/(k-1)倍，系数k通常可取0.2～1，则(k+2)/(k-1)的值约为3～∞，即的幅值是幅值的3～∞倍。双馈发电机定子侧无功功率可用下式表示，即：

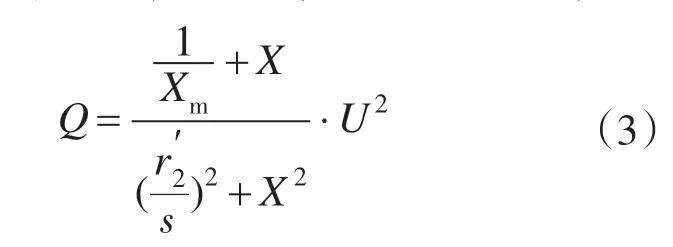
式中：Q为定子侧的无功功率；Xm为励磁电抗值；X为定子电抗X1与转子电抗X2归算至定子侧的值之和；s 为电机转差率为转子侧电阻归算至定子侧的值；U为定子侧的电网电压的有效值。

当上式中电机的参数一定时，无功功率的值将与U2成正比。即与补偿正序电压对应的无功功率是与负序电压对应的无功功率的9～∞倍。

若补偿后的正序电压与负序电压分别为和，并定义需要的电压补偿度为

则由前面的关系可得Δu+≫Δu-，也就是说对负序电压的补偿度相比于对正序电压的补偿度可以忽略不计。

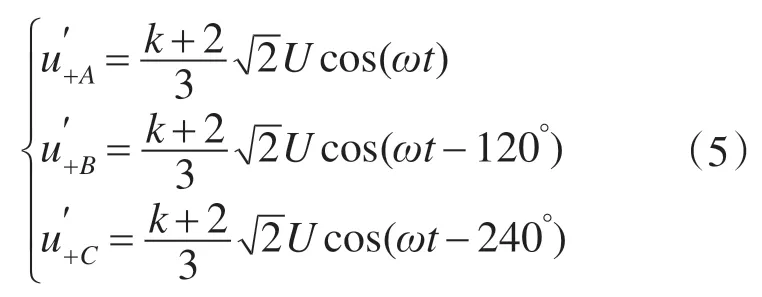
而故障电压的负序分量为

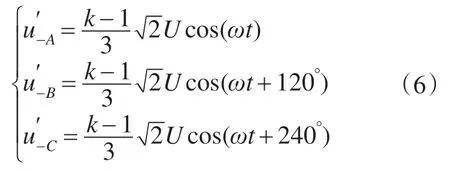
令正序电压恢复系数为p，即补偿后的正序电压为正常值的p倍，则有下式：

而负序电压保持不变，仍为式（6）。则补偿后的三相电压为

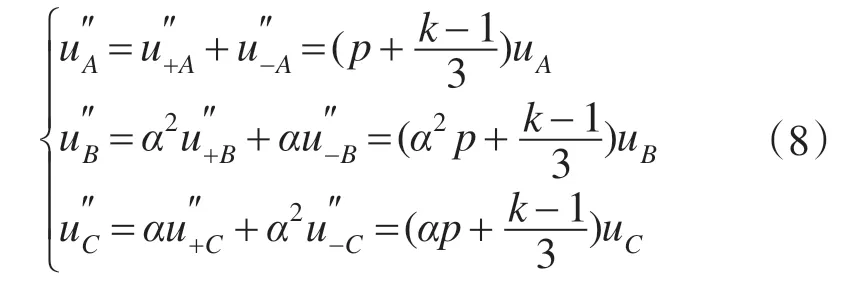
式中：α为120°旋转因子。

则补偿后的三相电压与正常值时的三相电压的幅值关系为

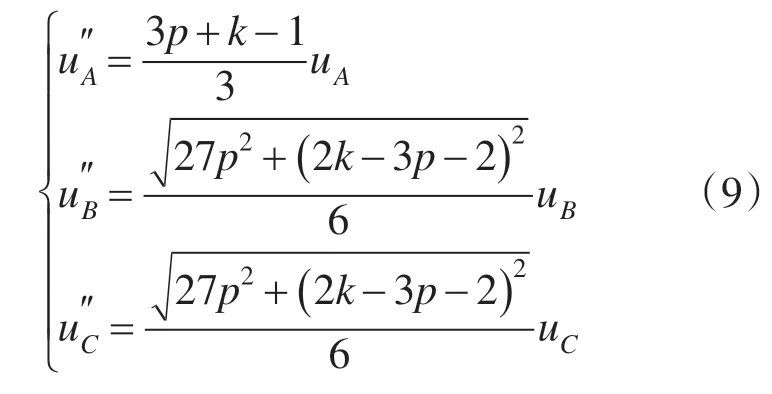
由上述可以看出，若仅仅将正序电压补偿至正常值（p=1）时，由于补偿阶段并没有将较小的负序电压消除掉，从而导致最终合成的电压情况为：故障相电压将低于正常值，而非故障相电压高于正常值，并且随着k的减小而愈加严重。从对称分量法的角度来分析，因为k越小，故障越严重，负序分量的比重也就越大，导致负序分量影响最终合成电压的效果就更加明显。

为了在补偿故障相电压的同时，不让非故障相发生过电压，依据故障穿越规范的要求，对非故障相电压进行限制，使故障期间的电压不超过正常值的125%，为了留有一定的裕量，将其限制为不能超过正常值的120%。则有

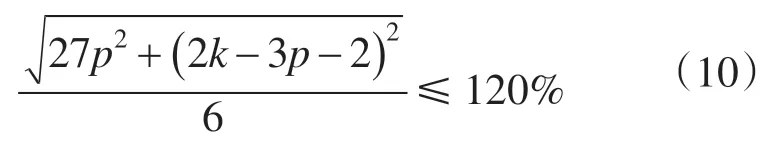
而要将故障相恢复至正常值，应使得下式成立，即：

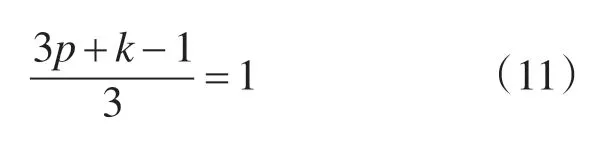
求解式（11），得到

当k在0.2～1 范围内取值时，按照式（12）所确定的p值并不全都满足式（10）。需要降低对故障相的恢复要求以保障非故障相不发生过电压。

经过相应的分析与调整可以得出确定正序电压恢复系数p的步骤为：将k代入式（11）确定出p，并记为p1，将k代入式（12）确定出p 并记为p2，则p最终的取值为

确定出p值也就意味着确定了正序电压的参考电压值。这样，只需相应的控制策略提供对应的无功功率，将故障时的正序电压补偿至所确定的参考电压值即可，不必同时考虑负序分量的影响。本文将该方法称为正序电压分量补偿法。使用该方法，将不对称故障情况下的补偿问题，简化为对电压正序分量的补偿，降低了系统的复杂程度。

3 实现正序电压分量补偿法的拓扑结构

在电网电压发生故障期间，为了快速恢复电网故障电压，网侧变流器GSC 将运行于STATCOM模式，从而为电网提供无功功率，以快速恢复故障电压。但影响了网侧变流器GSC 维持直流母线电压稳定的能力，而直流母线电压的不稳定又会反过来影响GSC 输出无功功率的能力，使电网电压难以快速恢复。其根本原因是维持直流母线电压稳定和向电网提供持续稳定的无功功率都是由控制网侧变流器GSC 来实现的，使二者之间相互耦合。因此，在故障期间，若将维持直流母线电压的稳定和向电网提供无功功率分别独立完成，将能够使故障电压快速恢复。

基于以上分析，在网侧变流器GSC的直流侧加入由DC-DC变换器控制的超级电容器，如图1所示。加入超级电容器之后，不论是否在故障期间，网侧变流器不再负责维持直流母线电压的稳定，而将此任务交由双向DC-DC 变换器进行控制。网侧变流器GSC的任务是在电网正常时，负责转子侧有功功率的传输，而在电网发生故障时，运行于STATCOM 模式，而此时由于有DC-DC 变换器控制的超级电容器，维持了直流母线电压的恒定，故而网侧变流器GSC可以很好地运行于STATCOM 模式，为电网提供持续稳定的无功功率，进而加快电网故障电压的恢复。达到了维持直流母线电压稳定和向电网提供持续稳定无功功率分别进行控制的目的。

图1 实现正序电压分量补偿法的拓扑结构Fig.1 Topology of implement the compensation method based on positive sequence voltage component

4 实现正序电压分量补偿法的控制策略

针对图1所示实现正序电压分量补偿法的拓扑结构，进一步研究其网侧变流器和DC-DC 变换器的控制策略。其中最为关键的是网侧变流器相应的控制策略。

与传统的网侧变流器GSC的控制相比较，图1 中所示实现正序电压分量补偿法的控制策略，主要是确定有功电流与无功电流的参考值，也就是在电网正常与故障情况下，合理确定有功与无功电流的参考值。

首先分析电网故障时的情况。此时网侧变流器GSC 将运行于STATCOM 模式，因此，在这种情况下的有功电流参考值为0。而对于无功电流参考值的确定，采用前面提出的正序电压分量补偿法。即在电网发生非对称故障时，按照式（10）～式（13）确定出相应的电压恢复系数p，从而确定出相应正序分量的参考电压其中为电网额定电压，p为前面提到的正序电压恢复系数。将此电压参考值与实际电网正序电压相减，差值经电压调节器之后得到故障情况下的无功电流参考值，如图2 所示的故障状态部分。从而控制网侧变流器提供无功功率，使发电机网侧电压的正序分量快速恢复至相应的参考值。

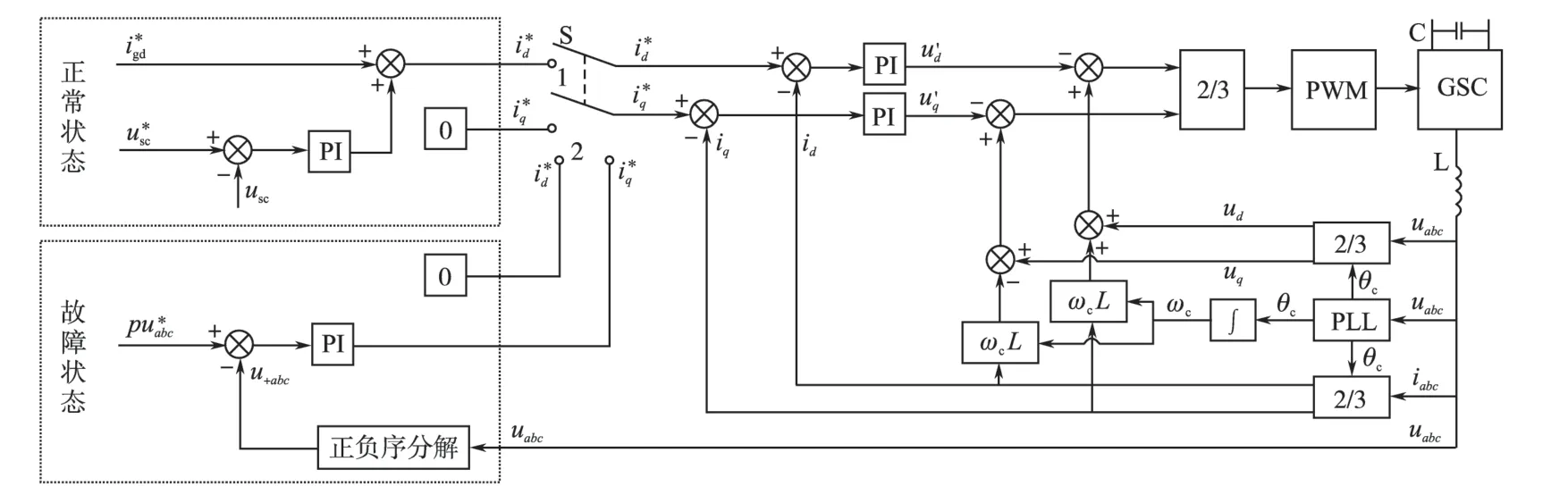
图2 网侧变流器的控制结构图Fig.2 Control diagram of GSC

其次对于电网电压正常的情况，网侧变流器GSC 直流侧的电压由超级电容器通过双向DC-DC变换器控制。当超级电容器工作电压低于其参考值时，网侧变流器GSC 向直流侧输送能量，使直流侧电压升高，直流侧对超级电容器进行充电，使超级电容器的电压升高。当超级电容器工作电压高于参考值时，其工作原理与之类似。

从以上的分析可以看出，在电网电压正常时，超级电容器的电压和直流侧电压是相互影响的。使直流侧电压的控制响应速度慢，波动较大，超级电容器充放电次数多。

为了克服上述问题，加入一个转子侧有功功率的补偿项，使引起直流侧电压变化的转子侧有功功率直接被网侧变流器GSC 交换到电网中，减小直流侧电压的波动，从而加快直流侧电压控制的响应速度，减少超级电容器充放电次数。

转子侧变流器RSC中交换的有功功率为

式中：Pr为转子侧变流器RSC 的有功功率；ura，urb，urc，ira，irb，irc分别为转子侧的三相电压与三相电流。

将Pr作为网侧变流器需要补偿的有功功率Pg，即

由式（15）计算出此时网侧的有功电流值igd，即有

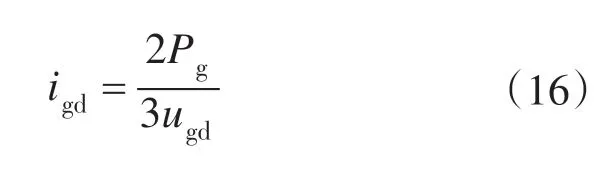
另外，在电网正常时，网侧变流器GSC 将间接影响超级电容器的电压稳定。通过超级电容器电压参考值与其实际值usc的差值经电压调节器之后，再与上述参考有功电流值相加，得到电网正常时的有功电流参考值。而无功电流的参考值设置为0。得到电网电压正常时，有功与无功电流参考值确定的结构框图如图2所示的正常状态部分。

在图2 所示网侧变流器GSC 的控制系统中，无功电流的参考值与有功电流的参考值的确定分为电网电压正常和故障两种情况。在电网电压正常的情况下，图2 中的开关S 接通至1 位置。而当电网发生不对称故障时，开关S 接通至2 位置。从而分别确定出电网电压正常和故障的情况下，相应的有功电流与无功电流参考值，实现网侧变流器GSC 控制状态的切换。

而对于双向DC-DC 变换器的控制，其控制策略与传统的控制方法一致，故此处不再赘述。

5 仿真分析

在Matlab/Simulink 环境下，搭建相应的仿真模型。其中，发电机的参数为：额定电压690 V，额定频率50 Hz，转子电阻0.005（标幺值），定子漏感0.171（标幺值），转子漏感0.156（标幺值），极对数3，参数均折算到定子侧。电网在3～3.625 s 发生单相的电压跌落，故障相为A 相，其电压跌落依次设置为80%，50%和20%。

为了说明问题，仿真分两种情况进行。情况1 为采用不加超级电容器的拓扑结构，网侧变流器GSC 采用传统的控制方式。情况2 是应用本文提出的正序电压分量补偿法，即采用图1 所示的拓扑结构，按照图2 和传统的DC-DC 控制策略进行控制。得到情况1 下的仿真波形如图3～图5 所示，而情况2 下的仿真波形如图6～图8所示。

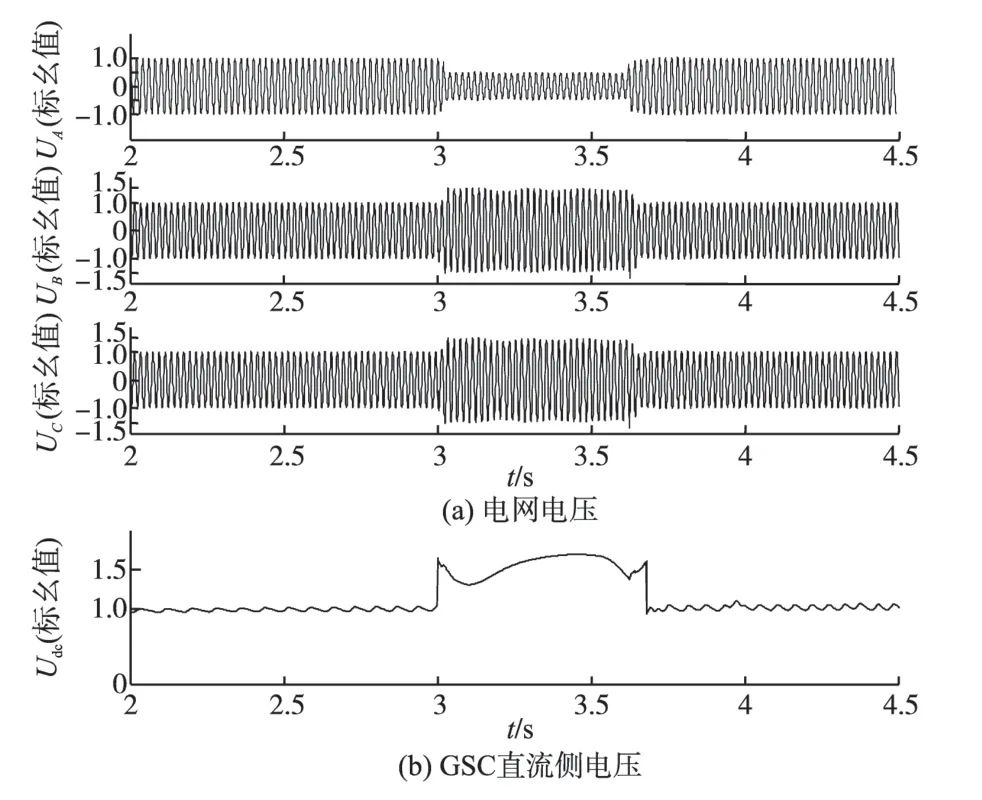
图3 情况1下A相电压跌落80%时的响应曲线Fig.3 Response curves with voltage dip 80%of A phase in case 1

图4 情况1下A相电压跌落50%时的响应曲线Fig.4 Response curves with voltage dip 50%of A phase in case 1

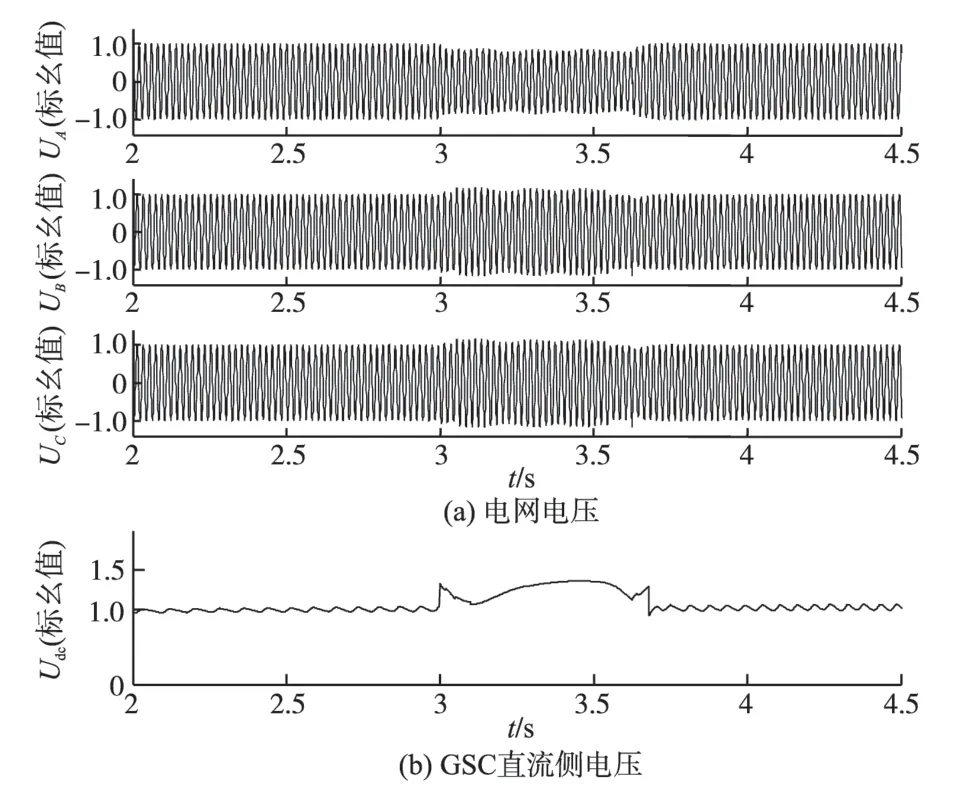
图5 情况1下A相电压跌落20%时的响应曲线Fig.5 Response curves with voltage dip 20%of A phase in case 1

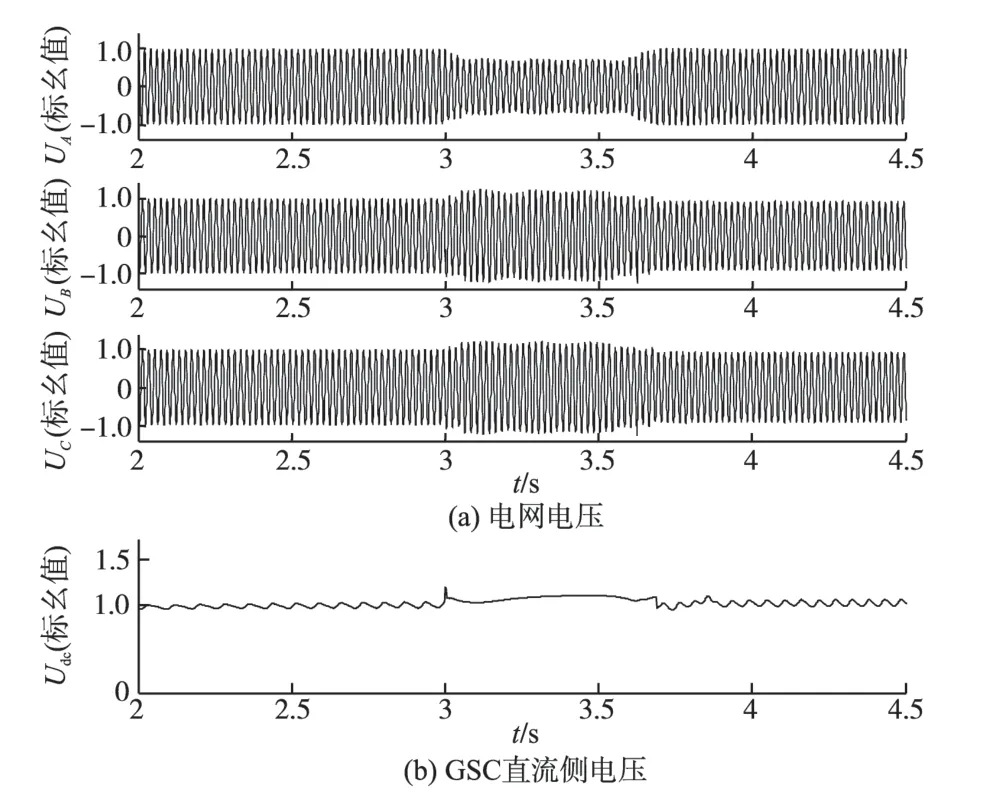
图6 情况2下A相电压跌落80%时的响应曲线Fig.6 Response curves with voltage dip 80%of A phase in case 2

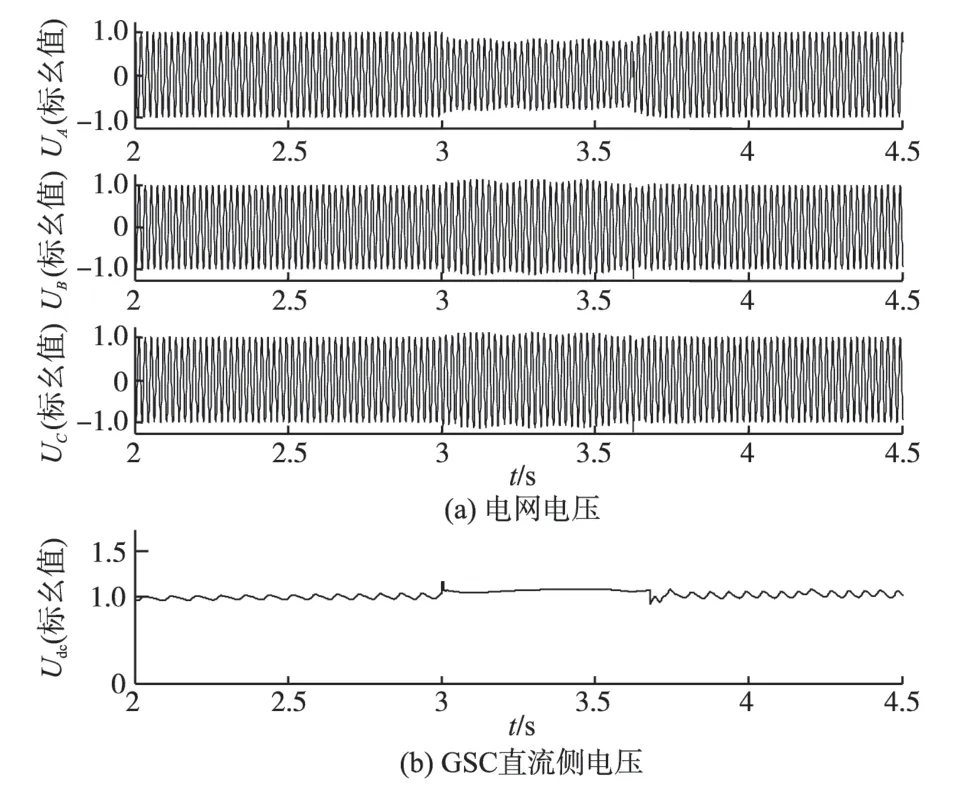
图7 情况2下A相电压跌落50%时的响应曲线Fig.7 Response curves with voltage dip 50%of A phase in case 2

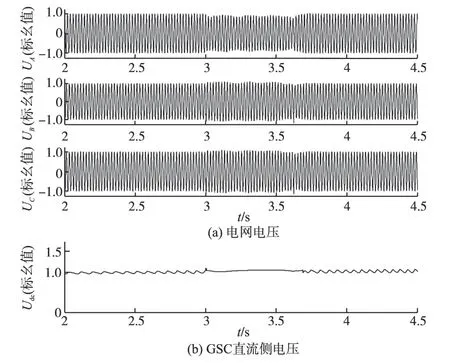
图8 情况2下A相电压跌落20%时的响应曲线Fig.8 Response curves with voltage dip 20%of A phase in case 2

在情况1下，当A相发生80%电压跌落时，由图3a可以看出，故障相电压仅恢复到额定电压的50%，非故障相电压为额定值的150%。A相发生50%电压跌落的情况，由图4a 可以看出，故障相电压恢复到额定电压的70%，非故障相电压为额定值的130%。对于A 相发生20%电压跌落的情况，从图5a 中可知，故障相电压恢复到额定电压的90%，非故障相则为额定值的110%。从图3b～图5b 可以看出，不同电网电压故障情况下，网侧变流器GSC直流侧电压为正常值的1.65～1.7倍。

在情况2 下，A 相发生80%电压跌落时，由图6a 可以看出，故障相电压恢复到额定电压的80%，非故障相电压为额定值的120%。在A相发生50%电压跌落的情况，由图7a 可以看出，故障相电压恢复到额定电压的90%，非故障相电压为额定值的110%。而对于A 相发生20%电压跌落的情况，从图8a 中可知，故障相电压恢复到额定电压的95%，非故障相则为额定值的105%。从图6b～图8b 可以看出，不同电网电压故障情况下，网侧变流器GSC直流侧电压在正常值的1.15倍以内。

对于两相故障的情况，经过仿真分析同样可以得到以上比较明显的现象，从而验证了该方法的合理性与正确性。

6 结论

本文提出一种正序电压分量补偿法，在电网电压出现非对称故障时，只需将正序电压补偿至所需要的参考电压值，从而将不对称故障问题简化为对称故障问题进行处理，简化了系统的控制策略。

各种故障情况下的研究结果表明，本文所述实现正序电压分量补偿法的拓扑结构和控制策略，以及正序电压的参考值的计算方法简单有效。

研究结果表明，采用本文的方法，在不同电压跌落程度的情况下，能够快速地恢复故障电压，降低发电机定子侧电压的不对称程度。如在电网电压跌落80%的情况下，可以将故障相的电压迅速地恢复至正常值的80%以上，同时保证非故障相电压不超过正常值的120%。

［1］贺益康，胡家兵.双馈异步风力发电机并网运行中的几个热点问题［J］.中国电机工程学报，2012，32（27）：1-15．

［2］贺益康，周鹏.变速恒频双馈异步风力发电系统低电压穿越技术综述［J］.电工技术学报，2009，24（9）：140-146.

［3］Zhang Shao，Tseng King-Jet.Advanced Control of Series Voltage Compensation to Enhance Wind Turbine Ride Through［J］.IEEE Transaction on Power Systems，2012，27：763-772.

［4］Wu Qiuwei，Xu Zhao，Jacob Stergaard.Grid Integration Issues for Large Scale Wind Power Plants（WPPs）［C］// IEEE Power and Energy Society General Meeting，2010：1-6．

［5］Xiang Dawei，Li Ran.Control of a Doubly Fed Induction Generator in a Wind Turbine During Grid Fault Ride-through［J］.IEEE Transaction on Energy Conversion，2006，21（3）：652-662.

［6］Flannery P S，Venkataramanan G.Evaluation of Voltage Sag Ride-through of a Doubly Fed Induction Generator Wind Turbine with Series Grid Side Converter［C］// IEEE Power Electronics Specialists Conference，2007：1839-1845.

［7］Erlich I，Wrede H，Feltes C.Dynamic Behavior of DFIGbased Wind Turbine During Grid Faults［C］// Power Conversion Conference，Nagoya，Japan，2007：1195-1200.

［8］Flannery P S，Venkataramanan G.Evaluation of Voltage Sag Ride-through of a Doubly Fed Induction Generator Wind Turbine with Series Grid Side Converter［C］// IEEE Power Electronics Specialists Conference，2007：1839-1845.

［9］栗然，唐凡，刘英培，等.双馈风电系统新型无功补偿与电压控制方案［J］.中国电机工程学报，2012，32（19）：16-23.

［10］Jorge Mart′ınez，Philip C Kjær，Pedro Rodriguez.Design and Analysis of a Slope Voltage Control for a DFIG Wind Power Plant［J］.IEEE Transaction on Energy Conversion，2012，27（1）：11-20.

［11］Kim Ki-Hong，Jeung Yoon-Cheul，Lee Dong-Choon.LVRT Scheme of PMSG Wind Power Systems Based on Feedback Linearization［J］.IEEE Transactions on Power Electronics，2012，27（5）：2376-2384.

［12］Kamran Masteri Farahani.PCC Voltage Control Using Flywheel System for Large Wind Farm［C］//2012 IEEE 7th International Power Electronics and Motion Control Conference-ECCE Asia，Harbin，China，2012：1283-1286.

［13］Kenneth E Okedu，Muyeen S M，Member.Wind Farms Fault Ride Through Using DFIG with New Protection Scheme［J］.IEEE Transactions on Sustainable Energy，2012，3（2）：242-254.

［14］Hansen A D，Michalke G，Sørensen P，et al.Co-ordinated Voltage Control of DFIG Wind Turbines in Uninterrupted Operation During Grid Faults［J］.Wind Energy，2007，10（1）：51-68.

［15］何鸣明，贺益康，潘再平.不对称电网故障下PWM 整流器的控制［J］.电力系统及其自动化学报，2007，19（4）：13-17.

［16］王宏胜，章玮.电网电压不对称故障条件下DFIG风电机组控制策略［J］.电力系统自动化，2010，34（4）：97-102.

［17］郑艳文，李永东，柴建云，等.不平衡电压下双馈发电系统控制策略［J］.电力系统自动化，2009，33（15）：89-93.

［18］胡家兵，贺益康，王宏胜.不平衡电网电压下双馈感应发电机转子侧变换器的比例-谐振电流控制策略［J］.中国电机工程学报，2010，30（6）：48-56.

［19］喻冲，宋平岗，刘鹏，等.不对称故障下双馈风力发电系统网侧变流器的控制方法［J］.大功率变流技术，2011（1）：27-30.

［20］郭晓明，贺益康，何奔腾，等.不对称电网电压下双馈风力发电机的直接功率控制［J］.电力系统自动化，2008，32（13）：86-91.