基于遗传算法的风电混合储能容量优化配置

杨国华，朱向芬，周鑫，丁晓花，卫宁波，马玉娟，王金梅

（1.宁夏大学电气工程与自动化系，宁夏银川750021；2.宁夏沙漠信息智能感知自治区重点实验室，宁夏银川750021）

1 引言

风能是一种清洁能源，但由于自然条件的变化，风速和风向不断的、随机的变化，导致风力发电输出功率具有不稳定性和不可预测性，直接影响微电网的调度运行，而通过风力发电系统和储能设备的协调配合，可以提高风力发电技术的可调度性和可控性。

近年来，混合储能的容量配置及控制策略得到广泛的关注。混合储能将容量小、寿命长、功率比较高储能环节与容量比较大、循环次数受限、相对能量比高、功率比低的储能环节结合使用，如将超级电容器与蓄电池混合。但是对混合储能的研究仍然处于初级阶段，而且研究主要集中在控制策略上，对容量配置的研究较少。目前对容量配置的研究大多按照经验配置混合储能的容量，未用定量的分析［1-2］。本文中风力发电系统的储能装置是蓄电池和超级电容器混合组成的，混合储能系统的容量配置是一个非线性规划问题，利用遗传算法进行求解，配置混合储能装置的全生命周期最小费用［3-8］。

2 模型分析

基于蓄电池和超级电容器混合储能独立风力发电系统的结构如图1 所示。当风速比较大时，储能装置处于充电状态，将电能存储起来；当风速比较弱或者峰值负荷时储能装置为负荷供电，以保证系统平稳连续的供电，提高供电可靠性。

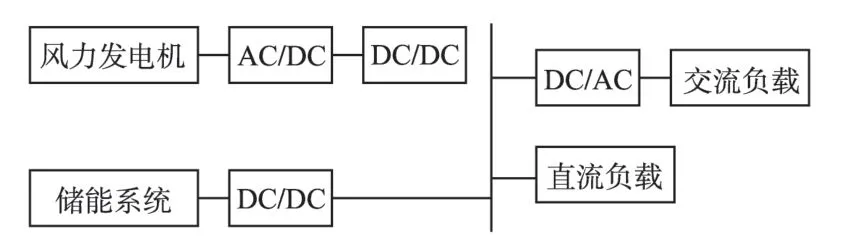
图1 独立风力发电系统的结构Fig.1 Structure of stand along wind generation system

2.1 蓄电池的模型

每个蓄电池的额定电压为Ub（V），额定容量为Cb（A·h），假设蓄电池组由m个蓄电池组成，则总的储能量Eb（MW·h）为

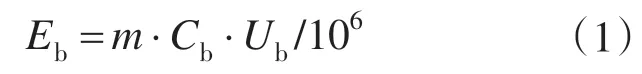
当蓄电池放电时，假设最大放电深度为DOD 时，则蓄电池组的最小的剩余储能量Ebmin（MW·h）为

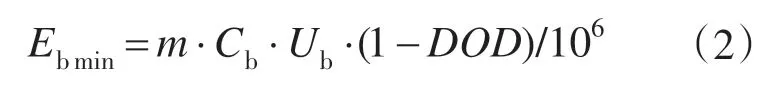
蓄电池通常以C10的时间率放电，则蓄电池组输出功率的额定值为

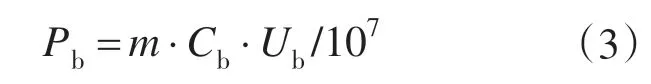
2.2 超级电容器的模型

每个超级电容器的端电压为Uc，电容值为Cc，假设超级电容器组由n 个超级电容器组成，则总的储能量为

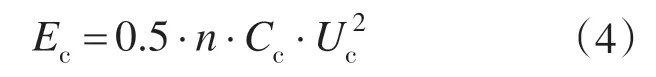
在实际情况中，超级电容器的工作电压有一个范围，记为Ucmin～Ucmax，则该超级电容器组的最大储能量为

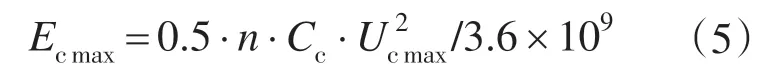
最小值为

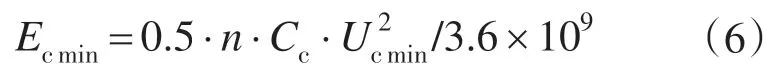
假设超级电容器工作电流的最大值为Icmax，则超级电容器组输出功率的最大值可表示为

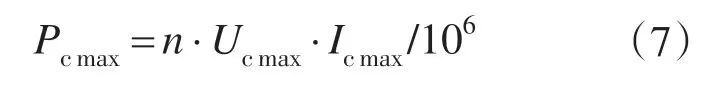
2.3 混合储能系统的充放电状态

系统中风电的输出功率Pw和负荷功率P1都有很大的波动性，导致随着时间的变化储能部分的储能量也在不断变化。

记不平衡功率为

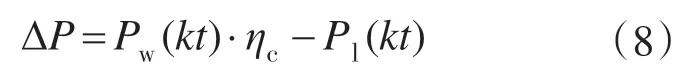
式中：ηc为风电系统中逆变器的功率转换率。

当ΔP＞0时储能装置处于充电状态，储能装置的储能量可以表示为

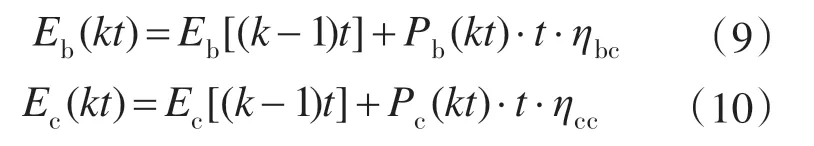
当ΔP＜0时储能装置处于放电状态，储能装置的储能量可以表示为

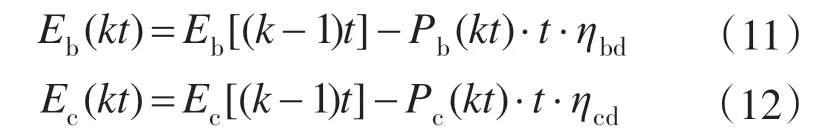
式中：Eb(kt)，Ec(kt)为在kt时刻蓄电池组和超级电容器组的储能量；Eb[(k-1)t]，Ec[(k-1)t]为(k-1)t时刻蓄电池组和超级电容器组的储能量；Pb(kt)，Pc(kt)为kt时刻蓄电池组和超级电容器组的充电和放电功率；ηbc，ηcc为蓄电池组和超级电容器组充电效率；ηbd，ηcd为蓄电池组和超级电容器组放电效率。

3 基于遗传算法储能容量的优化配置

基于蓄电池和超级电容器互补性，将二者混合使用。其中蓄电池承担不平衡功率ΔP中的基本部分，超级电容器承担不平衡功率ΔP 中的波动部分，以减少蓄电池的充放电次数，延长了蓄电池的寿命，改善了储能装置的性能，提高供电可靠性。

3.1 LPSP计算流程

风力发电系统的运行指标是负荷缺电率LPSP（loss of power supply probability），负荷缺电率LPSP 是负荷缺电量Elps 与负荷总需求量El 的比值。即

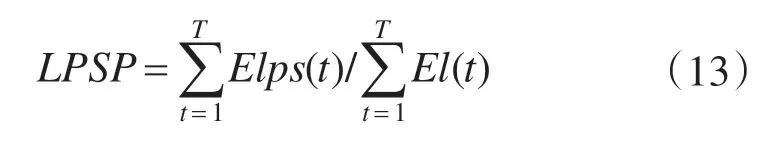
当风电功率满足负荷需求（ΔP>0）时，负荷缺电量Elps=0，储能装置充电，当风电功率不足（ΔP<0）时，储能装置放电补充电源功率的缺额，即

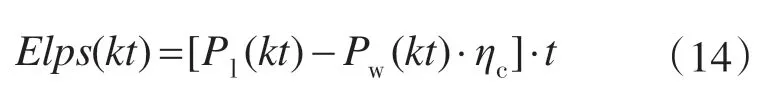
3.2 生命周期费用

IEC 60300—3—3（国际电工委员会制定的生命周期费用的计算标准）中的条例［9］规定设备的生命周期费用（life cycle cost，LCC）是指设备从规划、设计、制造、安装、使用、维修和废弃的整个过程中产生的总费用［10］。包括购买费用，拥有费用和处理费用即

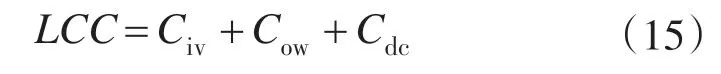
式中：LCC为生命周期费用；Civ为设备的购买费用；Cow为设备的拥有费用；Cdc为设备的处理费用（残值费用和报废费用）。

设备的生命周期费用中，购买费用随时间增长所占的比例下降，拥有费用随时间的增长而上升，在很多情况下，购买设备的费用低于生命周期的拥有费用，因此应该考虑设备的整个生命周期的费用，而不只是考虑初始价格，这样更符合实际情况，更具有现实意义。

储能系统优化的目标模型为购买费用、运行费用、维护费用和处理费用4大费用之和，即

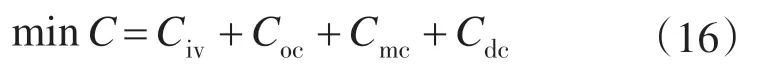
式中：Civ为购买费用；Coc为运行费用（包括实验、安装、损耗、人工费用等）；Cmc为维护费用（包括故障前后的维护费用）；Cdc为处理费用（包括报废费用和残值费用）。

3.3 优化约束条件

考虑独立风电系统的运行特性及储能系统的管理策略，建立约束条件如下：

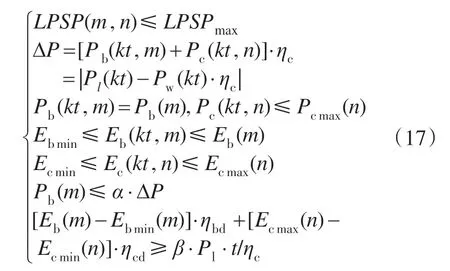
式中：m为储能系统中蓄电池的个数；n为储能系统中超级电容器的个数；α为不平衡功率中基本部分所占的比例；β为额定负荷中重要负荷所占的比例。

3.4 遗传算法

遗传算法是一种借鉴生物界的进化规律而演化来的高度并行、随机搜索和自适应寻优方法［11］。具有鲁棒性能好、方便用于解决离散且复杂的非线性问题等优点。正因为这些优点，使得遗传算法得到了非常广泛的应用。

遗传算法的流程如图2所示，步骤如下：

1）随机产生N个初始个体，构成初始种群；

2）计算每个个体的适用度函数值；

3）基于适用度函数值，选择、交叉和变异产生新一代群体；

4）判断种群是否停止条件，如果不满足返回第2）步，如果满足，执行下一步；

5）从当代群体中选择出最优个体作为优化问题的最优解。

图2 遗传算法流程图Fig.2 Flowchart of genetic algorithm

4 算例分析

假设某一风电示范工程规模为60 MW 的风电场，当地负荷为40 MW，逆变器效率为0.95，α为0.7，β为0.65，LPSPmax为0.05。现在要为其配置储能容量。具体参数见表1。

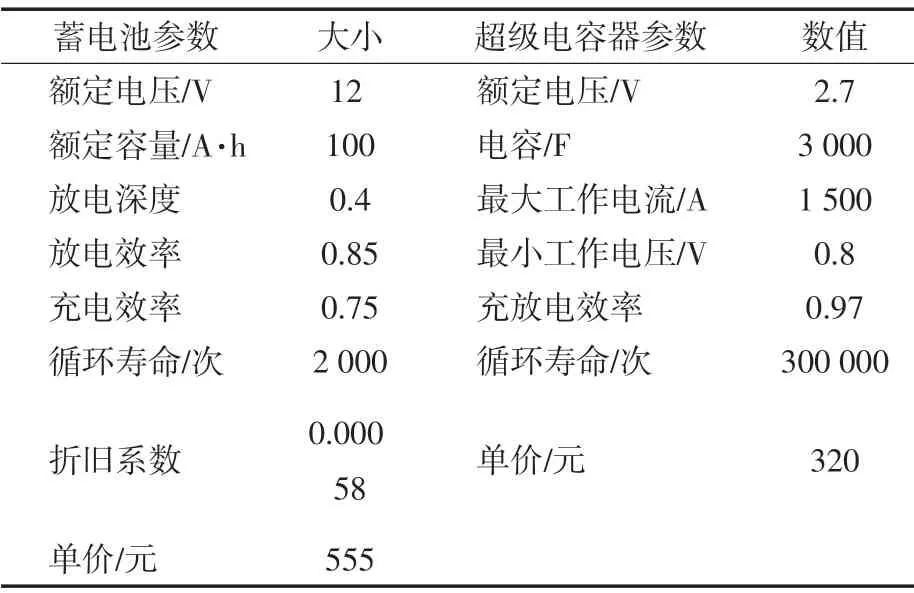
表1 储能系统的参数Tab.1 Energy storage system parameters

图3所示为某地风电输出功率和负荷功率在48 h 内的变化曲线，结合表1 所列蓄电池和超级电容器的参数及各项约束指标，优化目标在48 h里储能装置的总费用，运用遗传算法在Matlab环境下编程求解，得到了最优点近似值。优化后所得的详细值见表2。

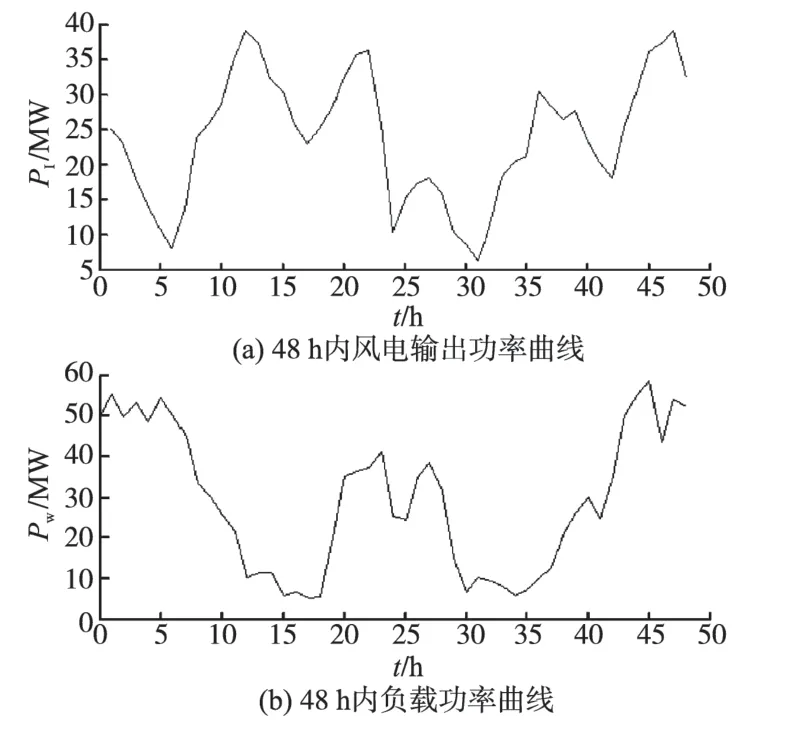
图3 48 h内风电输出功率/负荷功率曲线Fig.3 The curves of wind output power and load power in 48 h

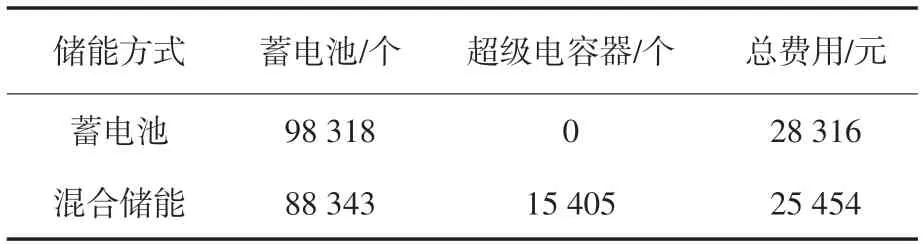
表2 2种储能方式的优化计算结果Tab.2 Optimization results of two energy storage modes

由表2可见，在相同的供电要求下，当单独使用蓄电池作为储能装置时，所用的最小费用为28 316 元，当蓄电池-超级电容器混合储能用作储能装置时，所用的费用为25 454 元，即在48 h内储能费用减少了2 862 元，降低了混合储能的成本，提高了整个系统的经济效益。

图4所示为48 h内两种储能装置的输出功率变化曲线，其中Pb曲线是蓄电池的输出功率变化曲线，Pc曲线是超级电容器的输出功率变化曲线，比较两条曲线看出蓄电池的输出功率比较少，这是由于系统中的不平衡功率主要由超级电容器承担，优化了蓄电池的工作状态，并使其使用寿命延长，从而降低了风电系统中储能装置的生命周期费用。

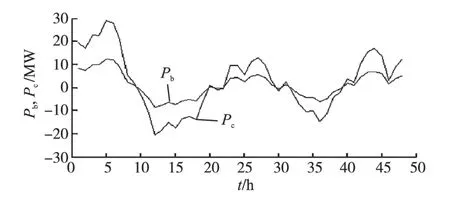
图4 蓄电池和超级电容器输出功率曲线Fig.4 The curves of battery and ultracapacitor output power

综上可知，蓄电池-超级电容器混合储能用作储能装置时，不仅降低了储能系统的生命周期费用，而且延长了蓄电池的使用寿命。

5 结论

基于遗传算法的风力发电系统储能容量优化配置研究充分考虑蓄电池和超级电容器的互补运行特性，优化了蓄电池的工作状态，提高了系统的整体的经济性。同时，以全生命周期费用理论为基础的储能优化目标，比只考虑购置成本的优化目标更具有实际意义。

［1］侯世英，方勇，孙韬，等.混合储能系统在独立光伏发电系统功率平衡中的应用［J］.电网技术，2011，35（5）：183-187.

［2］张国驹，唐西胜，齐智平.超级电容器与蓄电池混合储能系统在微网中的应用［J］.电力系统自动化，2010，34（12）：85-89.

［3］徐大明，康龙云，曹秉刚.风光互补独立供电系统的优化设计［J］.太阳能学报，2006，27（9）：919-922.

［4］胡希同，赵艳雷，张磊，等.风电功率调节系统储能变流器控制策略［J］.电测与仪表，2013，50（9）：41-45.

［5］Zhao Y S，Zhan J，Zhang Y，et al.The Optimal Capacity Configuration of an Independent Wind/PV Hybrid Power Supply System Based on Improved PSO Algorithm［C］//International Conference on Advances in Power System Control Operation and Management，2009：1-7.

［6］杨珺，张建成，黄磊磊，等.基于改进粒子群算法的独立光伏发电系统储能容量优化配置研究［J］.华东电力，2012，40（8）：1371-1374.

［7］何勇琪，张建成.独立型风光互补系统中储能容量优化研究［J］.电力科学与工程，2012，28（4）：9-13.

［8］杨珺，张建成，杜勋.并网风光发电中混合储能系统容量优化配置［J］.电网技术，2013，37（5）：1210-1216.

［9］IEC60300—3—3 Life Cycle Costing［S］.Beijing：China Standards Press，2004.

［10］崔新奇，尹来宾，范春菊，等.变电站改造中变压器全生命周期费用（LCC）模型的研究［J］.电力系统保护与控制，2010，38（7）：69-73.

［11］Deb K，Pratap A，Agarwal S，et al.A Fast and Elitist Multiobjective Genetic Algorithms：NSGA-II［J］.IEEE Transactions on Evolutionary Computation，2002，6（2）：182-197.