基于多传感器信号融合的数字滤波方法

陈晓燕，程志江，姜波，朱玉龙

（新疆大学电气工程学院，新疆乌鲁木齐830047）

1 引言

两轮自平衡车是一种基于倒立摆模型的自然不稳定体，具有非线性、多变量、强耦合等特点［1］，能够在外部的干扰下快速调整并始终保持平衡状态是其控制的关键。在实际控制过程中，分别采用陀螺仪和加速度计来测量角速度和角度信号，但由于陀螺仪存在随机漂移现象，且加速度计极易受车身运动干扰，因此，需要对车身的角度和角速度信号进行有效的滤波。采用简易互补滤波法［2］对陀螺仪和加速度计进行信号融合，平滑效果好，响应灵敏，但受陀螺仪温漂影响比较大。采用离散化低通滤波器与互补滤波相结合［3］的数据融合方法，抗干扰性能和移植性好，但是在微机电系统的精确度标定和温度补偿方面不完善。

本文在对两轮自平衡车进行数学建模的基础上，分析得出其平衡的关键是获取车身稳定的角度信号。通过对陀螺仪和加速度计的特性分析，发现陀螺仪是惯性器件，存在累积误差，需要利用加速度计的角度信号对陀螺仪进行周期性地修正，而加速度计存在动态误差，必须依靠陀螺仪积分后的角度信号进行修正［4］。因此，本文将卡尔曼滤波应用于自平衡车中，对陀螺仪与加速度计进行信号的融合。

2 自平衡车平衡原理

2.1 自平衡车动力学建模

自平衡车动力学模型如图1 所示，两轮自平衡车结构类似于传统的倒立摆，对其进行受力分析，包含驱动电机的输出转矩、地面支持力、摩擦力和惯性作用力所受的自身作用力影响。其中，车轮简化运动方程［5］可描述为

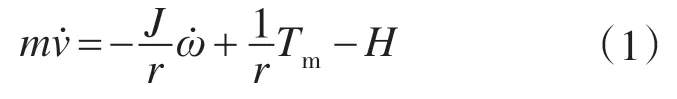
式中：m为小车质量；r为车轮半径；ω为车轮转速；v为车轮前进方向移动速度；J为车轮对车轴的等效转动惯量；Tm为电机电磁转矩；H为车体自身水平作用力。

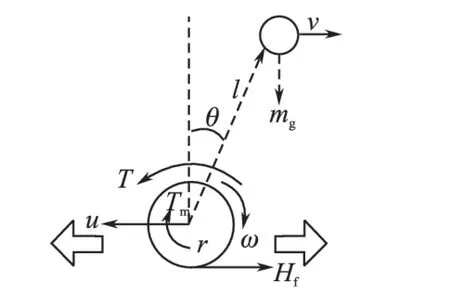
图1 自平衡车动力学模型Fig.1 Dynamic model of self-balanced car

对车体进行数学建模，其简化动力学方程［5］可描述为

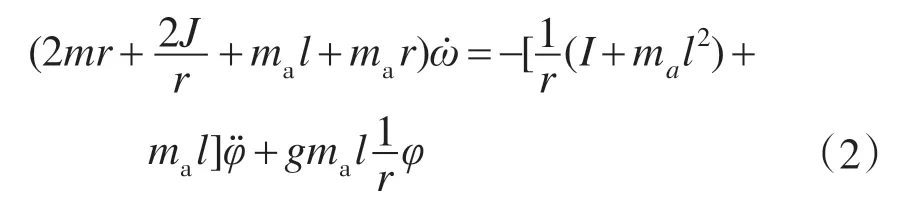
式中：ma为车体质量；I为车体对车轮等效转动惯量；φ为车体与垂直方向所成角度；T 为车轮对车身产生的转矩。

式（2）为两轮自平衡车关于车体倾角与角加速度的微分方程，由式（2）可知精确测量自平衡车倾角和倾角速度是控制自平衡车直立稳定的关键。

2.2 车身姿态检测

加速度计可用于测量物体的线性加速度，其输出值与倾角呈非线性关系，随着倾角的增加而表现为正弦函数变化，因此对加速度计的输出进行反正弦函数处理，才能得到其倾角值［6］。

式中：ΔV/Δg为加速度计灵敏度，mV/g；VOFFSET为加速度计的零偏电压。

采用陀螺仪对角速度进行检测，输出精度较好，但其存在漂移现象影响信号的可靠性，因此对陀螺仪测取的当前值与陀螺仪零点偏移量的差值经过比例转换后积分得到的数据即为角度信号，角速度计算公式为

式中，RGYRO为陀螺仪比例因子，其值选取太小波形存在滞后，选取太大则波形存在过冲现象，会引起车身震荡。

3 数据融合

在实际自平衡车运行过程中，车身运动引起的加速度会产生干扰信号叠加在测量信号上，影响两轮自平衡车角度输出信号的可靠性。而陀螺仪角速度积分转换为角度的过程长时间易形成积累误差，导致电路饱和，角度信号输出不准确。可采用卡尔曼滤波对加速度计和陀螺仪进行有效的融合，以得到准确的角度信息。

3.1 卡尔曼滤波

卡尔曼滤波是一种最优化自回归数据处理方法，它可以在未知模型性质的情况下，由上一时刻的状态值和当前的状态观测值来估计当前状态的估计值，从含有噪声的测量值中得到系统状态的最优估计。它提供了一种高效可计算的方法来估计过程的状态，并使估计均方误差最小。

在实际应用中，通常用离散化方程来描述连续系统，卡尔曼估计的离散时间过程包括离散随机差分方程和量测方程：

式中：A为k-1时刻线性映射到k时刻的状态矩阵；B 为控制输入变量的增益；H 为状态变量对测量变量的增益；wk-1，vk分别为过程激励噪声和观测噪声。

卡尔曼滤波包含状态预测和测量修正两部分，由滤波器估计过程某一时刻的状态，再以测量变量的方式获得反馈，更新流程如图2所示。

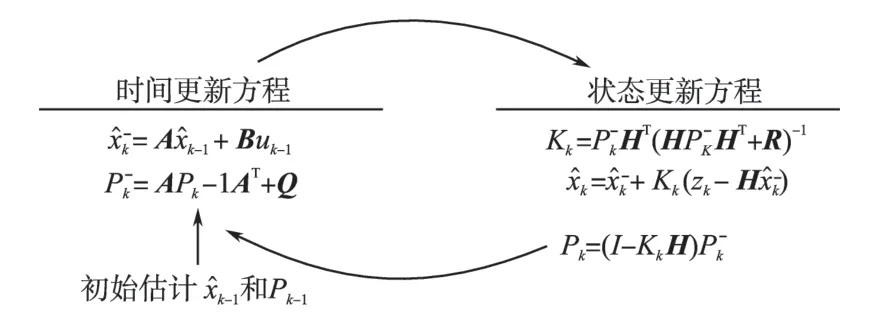
图2 卡尔曼更新流程图Fig.2 Kalman update process

状态更新方程及时地由当前系统状态和噪声方差估计出下一步系统状态，测量更新方程负责反馈，将新的测量信号加入已由状态更新方程得出的先验估计状态，最终得到系统状态的后验估计。

3.2 姿态信息融合

系统以陀螺仪、加速度计来检测车身所处的俯仰状态和状态变化率，卡尔曼滤波可以根据陀螺仪和加速度计不同的数学模型，通过建立方程来消除测量误差。由于角速度与角度存在微分关系，故将加速度计作为观测变量，陀螺仪作为先验估计变量，由加速度计测得角度值对陀螺仪积分后的角度信号进行对比和修正，从而把卡尔曼滤波器应用到了两轮自平衡车姿态检测的角度与角速度数据处理中。

首先，将陀螺仪的输出量看成是由输出真值和偏差组成，由陀螺仪偏差值eθ′获取陀螺仪的角速度信号：

式中：θ′为去除偏差的角速度；θm′为陀螺仪测量角速度。

若偏差不存在，则eθ′=0。过程协方差矩阵微分方程为

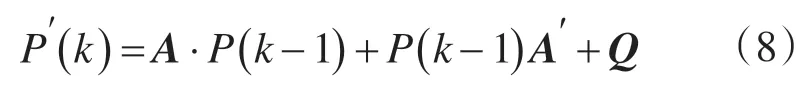
由于过程的状态不随时间改变，本系统令矩阵

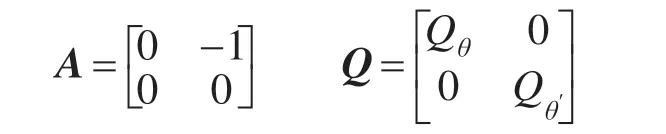
式中：A为系统参数；Q 为过程噪声协方差；Qθ，Qθ′分别为加速度计和陀螺仪的协方差。

将去除偏差的两轮自平衡车倾斜角速度进行积分便可以得到其倾角值：

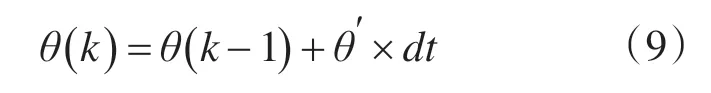
式中：θ(k-1)为前一时刻的角度信号，其零时刻的初始值可随意给定；θ(k)为当前时刻更新的角度值；dt为卡尔曼采样频率。

其协方差更新为

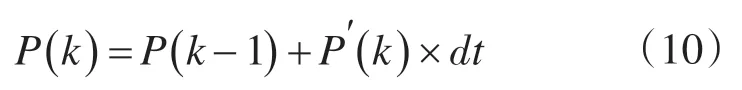
式中：P(k-1)为前一时刻的协方差；P(k)为当前时刻协方差。

初始值P(k-1)可随意给定（P≠0），系统会逐渐收敛，式（1）和式（2）则为对系统的预测。卡尔曼增益为

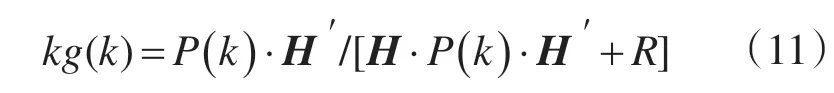
由于陀螺仪积分得到的角度与加速度计测得的角度信号相对应，则′表示H 的转置，矩阵R为测量噪声协方差，由观测得到。更新的角度偏差为eθ=θ-θ(k)，结合预测值和测量值，可以得到角度最优化估算值：

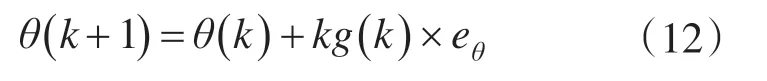
协方差更新为

计算完时间更新方程后，将更新的角度最优估计值和协方差作为下一次计算的先验估计，循环估计下一步的系统运行状态［6-9］，以此反复进行即可得出系统最优的角度信号值，其程序流程图如图3所示。

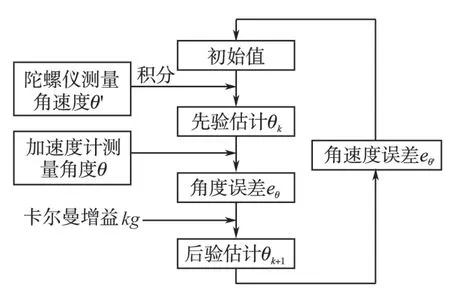
图3 卡尔曼控制流程图Fig.3 Kalman control process

基于离散的卡尔曼滤波原理，将加速度计得到的角度信号与陀螺仪得到的角速度信号送入卡尔曼滤波器中进行信号的融合，以获得更加精确的角度信号，再对滤波所得的角度信号进行比例和微分控制后，即可输出作为角度控制的电压输出量，用于驱动电机，从而实现两轮自平衡车的直立控制。其控制过程如图4所示。

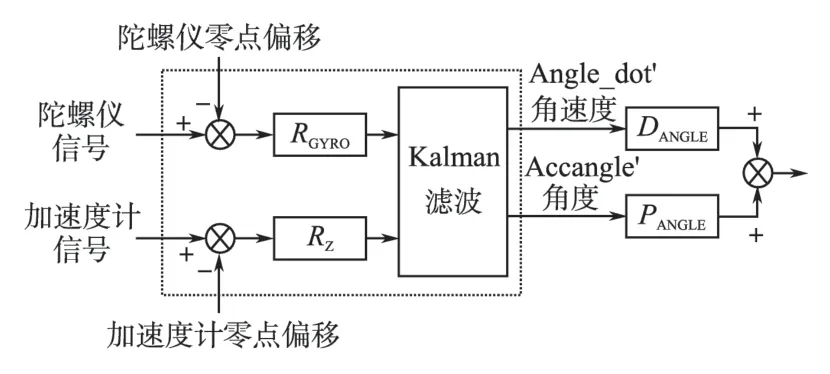
图4 车身姿态检测原理图Fig.4 Attitude detection principle of self-balanced car

4 卡尔曼滤波的实现

在两轮自平衡车控制的过程中，速度传感器采用光电编码器检测当前车速，而倾角传感器采用陀螺仪与加速度计控制车体角度，并将这些采集到的转速控制信号与角度控制信号送入核心控制单元MCU 进行数据处理后，叠加加载到两后轮电机上，控制2个电机的正反向运动，以实现两轮自平衡车的静止和直立行走。其硬件控制结构如图5所示。

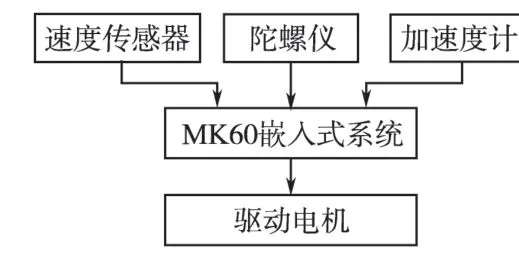
图5 硬件控制结构图Fig.5 The hardware control structure

为了获得稳定准确的数据，通过单片机软件多次采集自平衡车静止时模拟通道的AD采样数据，取平均值作为倾角信号的零偏电压，将陀螺仪与加速度计的测量数据分别与相应零偏电压做差，经过16位精度比例转换为角速度与角度信号后，送入MK60 嵌入式系统进行控制。上位通过无线串口示波器实时观察车体的滤波情况。

当两轮自平衡车处于直立状态时，由于噪声的干扰，滤波前角度与角速度信号曲线均在零度水平线±10°上下波动，波形震荡频率高，车身稳定性差；经过卡尔曼滤波后波形保持在零度水平直线状态，曲线光滑平稳，车身稳定性高，零点放大图如图6所示。

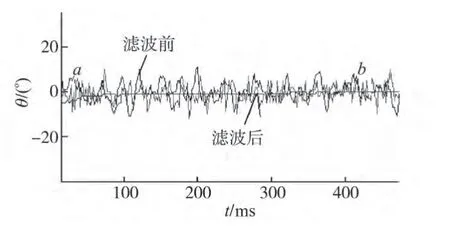
图6 零点放大图Fig.6 Zero point enlarge figure

车身倾角变化时，由于两轮自平衡车自身稳定性差，滤波前波形存在过冲现象，过冲角度高达±8°，会引起车身震荡。经过卡尔曼滤波后，车身角度信号过冲现象消除，且跟随性好，实时反应了车身倾角变化情况。滤波对比图如图7所示。

而角速度代表了角度的变化量，在角度变化的同时角速度产生一个脉冲信号，其高度反应了角度变化的快慢。当角度不再变化时，角速度则立刻回复到原点，两轮自平衡车保持此倾角运行。卡尔曼滤波图如图8所示。

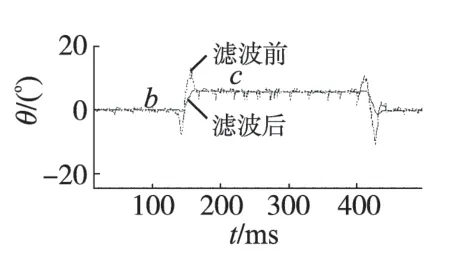
图7 角度滤波对比图Fig.7 Angular filtering contrast figure

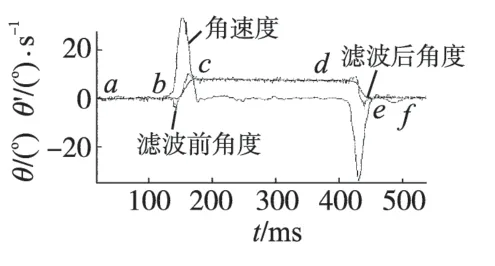
图8 卡尔曼滤波图Fig.8 Kalman filtering

由上述分析可知，加速度计得到的角度信号反应了两轮自平衡车角度的变化情况，随时跟随角度的变化；而陀螺仪得到的角速度信号反应了角度变化的灵敏情况，两轮自平衡车倾角改变后陀螺仪信号变化，随即会立即回复到原处。经过卡尔曼滤波后的角度信号基本不存在谐波，且波形平滑，滤波效果好，提高了两轮自平衡车的稳定性。

5 结论

针对两轮自平衡车姿态检测传感器陀螺仪输出角速度存在随机漂移误差，且极易受外界噪声干扰的问题，本文采用卡尔曼滤波算法将陀螺仪和加速度计输出的信号进行数据融合，来估计系统的最佳状态。在动态数据采集试验的基础上，通过卡尔曼滤波有效地补偿传感器漂移与测量噪声等因素对加速度计与陀螺仪的影响，减小了姿态角度测量误差，提高了运算精度，因而有效地提高了两轮自平衡车的稳定性。

［1］姜香菊，刘二林.两轮自平衡机器人角度检测数据融合算法［J］.计算机工程与应用，2013，49（8）：203-205.

［2］张吉昌，程凯，郑荣儿.单轴双轮自平衡车姿态检测方案设计［J］.中国海洋大学学报，2009，39（S）：467-470.

［3］夏圣，许勇.基于MEMS 组合模块的姿态检测系统设计［J］.单片机与嵌入式系统应用，2011（4）：52-55.

［4］江杰，朱君，岂伟楠.四旋翼无人飞行器姿态数据采集处理系统［J］.计算机测量与控制，2012，20（6）：1703-1706.

［5］Han I，Park H S，Jeong Y K，et al.An Integrated Home Server for Communication，Broadcast Reception and Home Automation［J］.IEEE Transactions on Consumer Electronics，2006，52（1）：104-109.

［6］冯智勇，曾瀚，张力，等.基于陀螺仪及加速度计信号融合的姿态角度测量［J］.西南大学师范大学学报：自然科学版，2011，36（4）：137-141.

［7］Kalman R E.A New APProach to Linear Filtenng and Prediction Problems［J］.Transaction of the ASME-Journal of Basic Engineering，1960，82（Series D）：35-45.

［8］焦勇，杨庆堂.两轮自平衡机器人的姿态检测系统的设计［J］.船电技术应用研究，2011，31（5）：45-49.

［9］LIU Kun，BAI Ming，NI Yuhua.Two-wheel Self-balanced Car Based on Kalman Filtering and PID Algorithm［C］//Proceeding of 2011IEEE the 18thInternational Conference on Industrial Engineering and Engineering Management（Volume1）2011：281-285.