浅谈“无棱”二面角的解法

王 丹

(鄂南高级中学，湖北 咸宁 437100)

浅谈“无棱”二面角的解法

王 丹

(鄂南高级中学，湖北 咸宁 437100)

二面角问题是历年高考考查的热点，也是难点。求二面角的基本步骤是作、证、算，即先作出一个平面角，再证明这个角就是所求二面角的平面角，最后将这个平面角放在一个三角形中计算求解，其中作出二面角的平面角是关键。所谓“无棱”二面角，是指所给二面角的两个面直观上只有一个公共点，而不是一条公共直线(即二面角的棱)，这就大大增加了求二面角的难度。本文通过一道例题介绍“无棱”二面角的常规求法，以供参考。

例：如图1所示,在边长为ɑ的正方体ABCD-A1B1C1D1中，点E、F分别是AB、C1D1的中点，求平面ADD1A1与平面DEB1F所成的二面角(锐角)的余弦值。

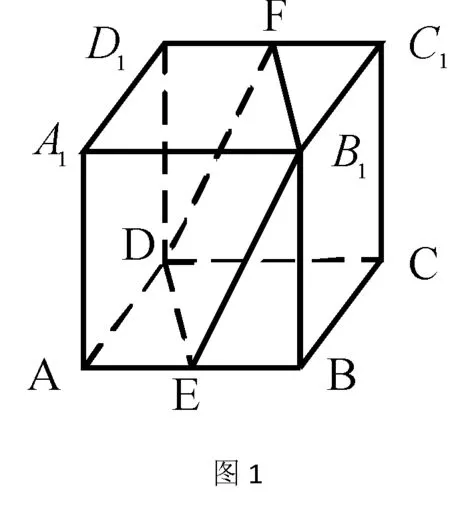
一、由“无棱”向“有棱”转化

法1(补形法) 找(作)出二面角的棱的常用方法是两点法(根据两点确定一条直线，找到所求二面角的棱)

解析：延长B1F、A1D1，设两延长线交于点G，连DG、A1D、B1D，则DG为平面ADD1A1与平面DEB1F的交线。

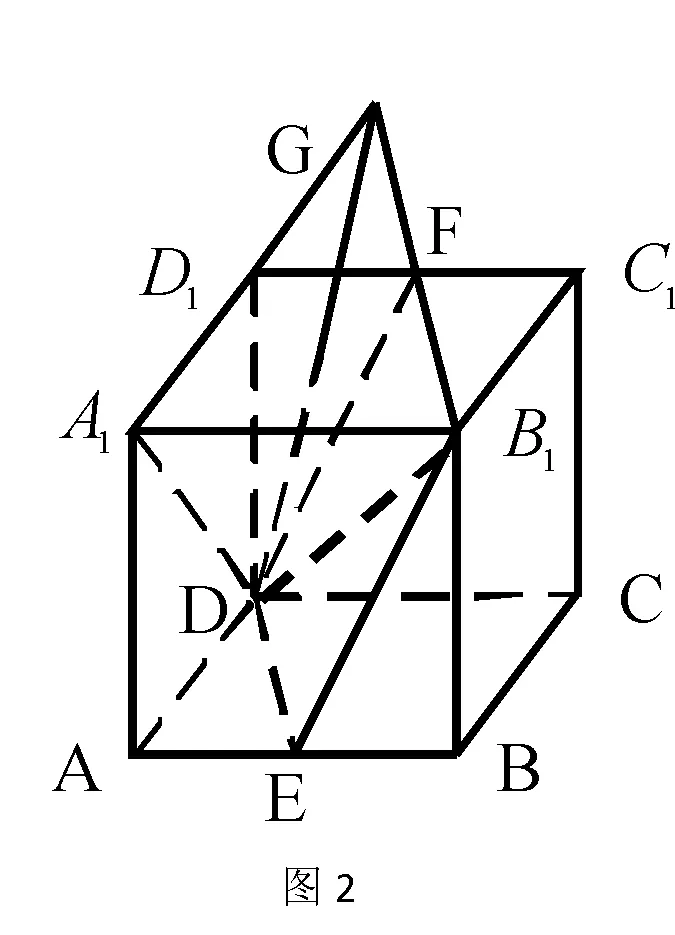
∵A1D1=D1G=D1D且D1D⊥A1G，

∴A1D⊥DG，∵A1B1⊥ 面A1D1DA，

∴A1B1⊥DG，∴DG⊥A1B1DDG⊥DB1，

∴∠A1DB1就是所求二面角的平面角。

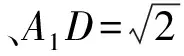
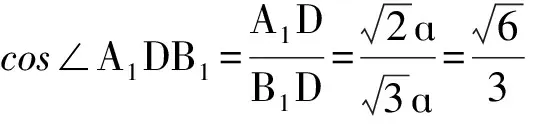
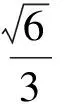
评注：将“无棱”问题转化为“有棱”问题，实际上是将难求二面角问题转化为易求二面角问题。

法2(平移法) 根据“两平面平行，同位二面角或内错二面角相等”可以将“无棱”二面角的一个面平移到适当位置，得到一个与所求二面角相等或互补的有棱二面角，然后找(作)出该二面角的平面角即可。

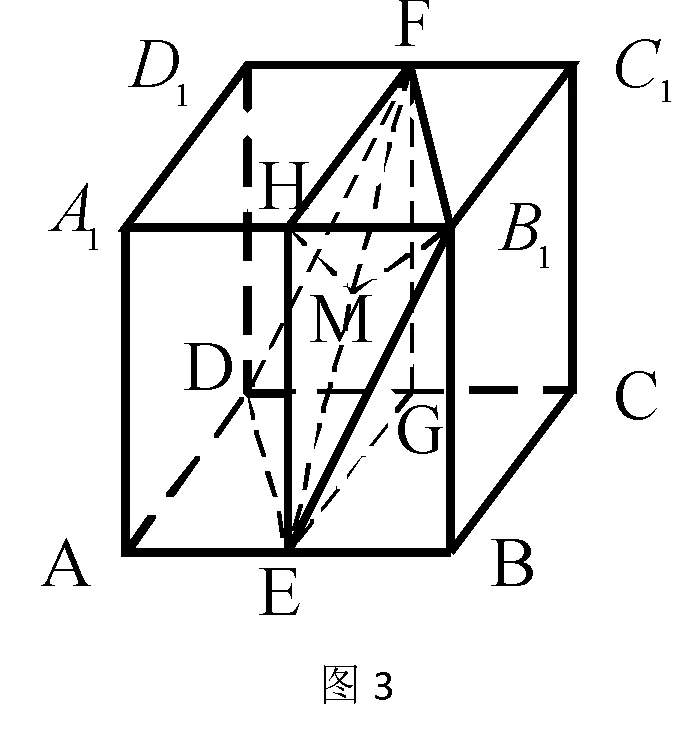
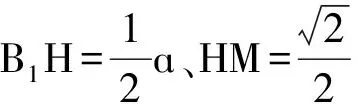
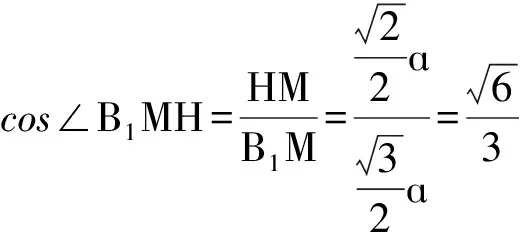
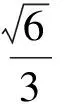
评注：寻找面面平行是关键，而面面平行常由线线平行得到。

二、避开找棱问题

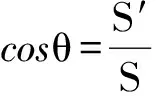
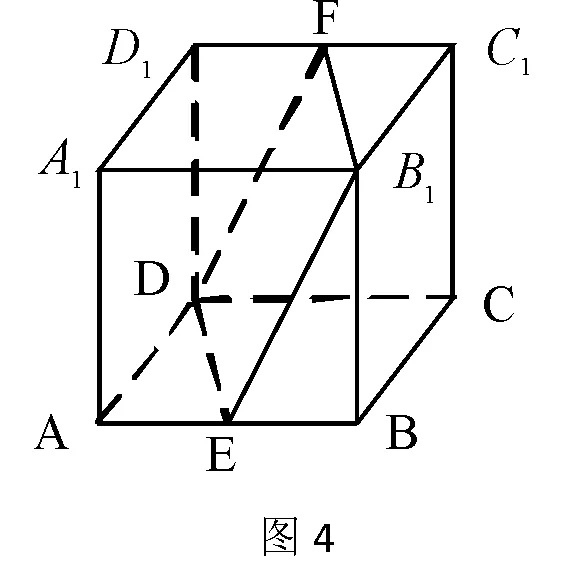
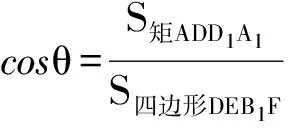
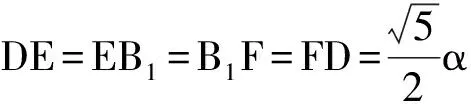
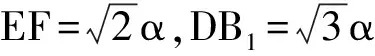
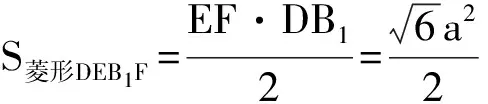
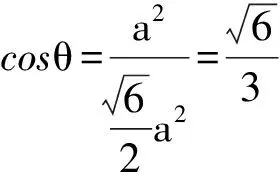
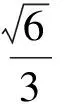
评注:找(作)出一个半平面内的三角形(或四边形)在另一个半平面内的射影，再利用面积射影定理求解。关键是找射影及求面积。

法4(公垂面法) 其理论依据是：作出二面角ɑ-l-β两半平面的垂面γ，或证明平面γ是α、β的公垂面，可由公垂面γ与二面角两半平面α、β交线的夹角求得二面角的大小。

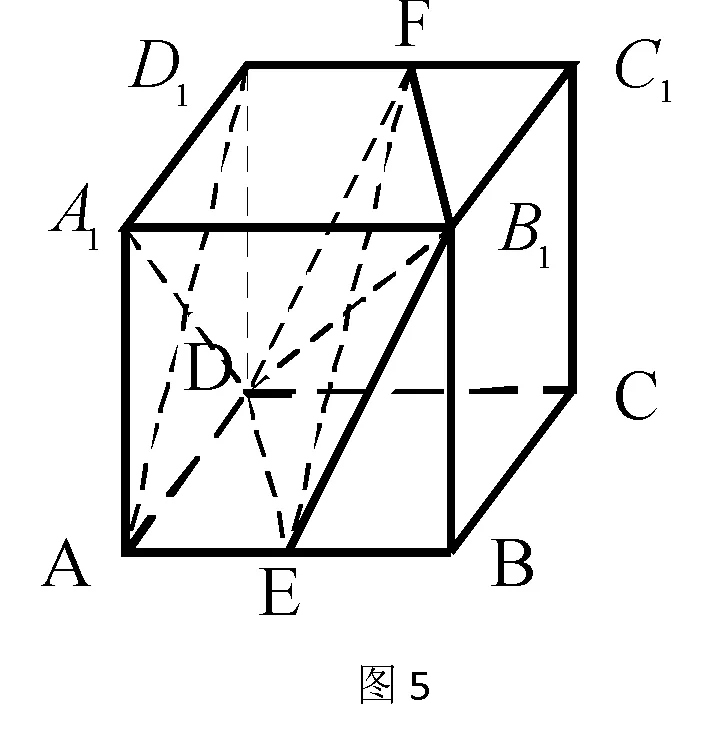
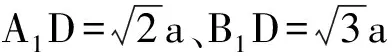
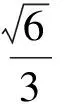
评注：证得面面垂直是关键。

法5(向量坐标法) 借助向量工具，将二面角的问题转化为两半平面的法向量的夹角问题研究。

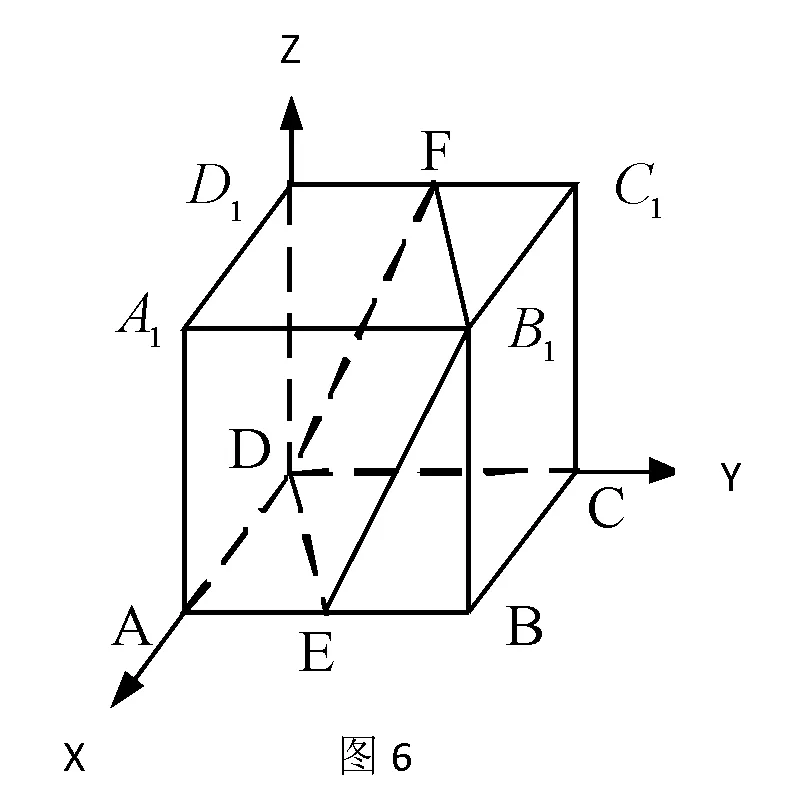
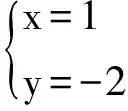
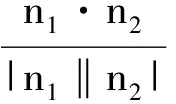
评注：利用向量坐标法求解时，首先应合理建立空间直角坐标系，找两个半平面的法向量是关键，一定要将二面角的平面角与两个半平面法向量夹角的关系弄清(相等还是互补)，坐标法将严密的逻辑推理转化为坐标计算，一般很少添加辅助线，但计算繁琐且易出错。

事实上，无棱二面角并不可怕，它还有其它的求法，如补体法、垂线法等，我们要根据题型，选择合适的解法。求解无棱二面角问题时，可按如下步骤进行：先通过补形或平移面的方式寻找二面角的棱，再利用二面角的定义或三垂线定理(或逆定理)作二面角的平面角，求得二面角的大小。若作棱有难度，可考虑面积射影法、公垂面法、空间向量坐标法等。值得注意的是，利用三垂线定理或面积射影定理都只能求锐二面角，所以，要清楚所求的是锐二面角还是钝二面角以及得到的角的大小与所求二面角的大小关系(相等或互补)，这样，才能准确求出问题中的二面角的大小。

[1]刘绍学.普通高中课程标准实验教科书·数学2(必修A版)[M].北京：人民教育出版社，2010.

[2]周远方，孙延洲.高中课堂教学标准及教学实例[M].武汉：湖北教育出版社，2013.

[3]吴天德.从一道高考题中探究无棱二面角的求法[J].中学数学月刊，2012(11).

[4]何建民.例谈无棱二面角的求法[J].数学教学研究月刊，2005，(11).

2095-4654(2015)08-0202-03

2015-03-15