基于同步运移理论的瓦斯抽采气固耦合数值模拟

张美红,吴世跃,牛 煜,孟晓红

(太原理工大学 矿业工程学院,太原 030024)

基于同步运移理论的瓦斯抽采气固耦合数值模拟

张美红,吴世跃,牛 煜,孟晓红

(太原理工大学 矿业工程学院,太原 030024)

以煤层瓦斯扩散渗流同步运移理论为基础,综合考虑瓦斯抽采过程中煤体变形引起的孔隙率、渗透率变化,建立了瓦斯抽采气固耦合动态数学模型。以晋城某矿为例,结合该矿煤层赋存特征,借助Comsol multiphysics软件进行了数值模拟,模拟结果表明在瓦斯抽采过程中有效抽采半径与抽采时间符合幂函数关系;随着煤层埋藏深度增加,上覆应力增大,煤层孔隙率和渗透率降低,是导致瓦斯抽采难度增加的主要原因,为此如何能提高煤层的渗透率和孔隙率是增加瓦斯抽采率的关键;单纯增大抽采负压对提高瓦斯抽采率影响不大。该研究结论为优化瓦斯抽采工艺参数提供了理论依据。

同步运移;瓦斯场;煤体变形;瓦斯抽采;数值模拟

随着煤层开采深度的增加,地应力对瓦斯运移的影响越来越大。近年来,学者们应用流固耦合理论研究瓦斯抽采过程中的瓦斯运移及煤体变形。[1]司鹄等[2]在多孔介质渗流基础上建立了顺层钻孔条件下的流固耦合数学模型并通过数值模拟确定了瓦斯抽采工艺中相关参数;赵阳升等[3]建立了均质煤层条件下的气固耦合数学模型;梁冰等[4]建立了考虑温度场作用下的气固耦合的数学模型;周军平等[5]建立了考虑孔隙压力、有效应力及基质收缩的耦合模型,但未考虑气体在煤体中吸附、解吸所引起的膨胀收缩;杨天鸿等[6-7]建立了考虑煤层吸附、解吸作用的含瓦斯煤岩固-气耦合模型;Connell[8]在煤层是各向异性介质基础上,通过煤层渗透率变化规律,对瓦斯运移变化规律进行了深入研究。现有流固耦合模型研究中大多数学者认为煤层中瓦斯运移的历程是吸附气体解吸、由孔隙向裂隙扩散及裂隙内渗流三个连续过程,而事实上孔隙内扩散过程是与此连续过程同步发生的。[9]本文在考虑煤体变形对孔隙率和渗透率影响的基础上,强调了煤层中瓦斯运移的扩散、渗流同步性,并依此建立瓦斯抽采气固耦合动力学模型,最后通过数值模拟的方法揭示瓦斯抽采工艺的主控因素。

1 瓦斯抽采气固耦合模型

在瓦斯抽采过程中,吸附在孔隙及裂隙表面的瓦斯在浓度梯度作用下解吸出来,一部分气体在孔隙内连续扩散,另一部分气体由孔隙扩散到裂隙中,与其中游离状态瓦斯在压力梯度作用下一起宏观渗流。也就是说气体不论是在孔隙内发生解吸扩散还是扩散到裂隙内参与宏观渗流都是同步发生的。基于以上考虑现对该物理模型作进一步假设:

1) 煤岩体中瓦斯为理想气体,其吸附解吸过程符合Langmuir吸附方程,在孔裂隙中的运移满足菲克扩散方程和达西渗流定律。

2) 瓦斯抽采过程中孔隙系统和裂隙系统压力瞬间达到平衡状态,忽略两系统间的质量交换。

3) 忽略煤层内水相流动。

4) 煤岩体的变形由煤岩体内骨架变形和孔隙体积变形构成。

5) 煤岩为均匀,各向同性的线弹性体。

2 瓦斯抽采流固耦合数学模型

瓦斯抽采是一个煤岩变形和瓦斯运移相互作用过程,为揭示抽采过程中瓦斯渗流机理,建立瓦斯抽采气固耦合数学模型。

2.1 渗流场方程

2.1.1 Langmuir吸附方程

煤岩体为多孔介质且具有很强的吸附作用,瓦斯以单层物理吸附状态赋存在煤岩体中[10-11],符合Langmuir吸附方程。

(1)

式中:C为单位体积煤层所含吸附状态煤层气的质量,kg/m3;p为吸附平衡压力,MPa;a为吸附常数，表示在给定温度下,单位质量固体的极限吸附量，m3/t;b为吸附常数，MPa-1;c为单位体积煤中可燃物质量,t/m3;pn为一个标准大气压,MPa;R为气体常数;T为煤体的温度,K。

2.1.2 菲克扩散方程和达西渗流定律

煤层是孔隙—裂隙二重介质,吸附在孔隙及裂隙表面的瓦斯,其运动服从裴克扩散方程;游离在裂隙中的瓦斯,其流动服从达西渗流定律。

(2)

式中:D称为扩散系数,m/s.

(3)

式中:v为渗流速度,m/s;K为渗透率,m2;μ为粘度,MPa·s;p为压力梯度。

2.1.3 连续方程

根据扩散、渗流质量守恒定律可得考虑同步过程的瓦斯渗流场方程:

(4)

式中:ρ为气体密度,kg/m3;v为渗流速度,m3/s;n为孔隙度,%;C为吸附状态瓦斯,kg/m3。

将公式(1-3)带入(4)中得出瓦斯抽采过程中渗流场方程:

(5)

2.2 应力场方程

瓦斯抽采气固耦合模型中的应力场方程主要由应力平衡方程、煤岩变形的应力-应变关系的广义Hooke定律、本构方程、几何方程及考虑瓦斯气体在煤岩体中吸附、解吸所引起的膨胀收缩的应变方程构成,联立可得瓦斯变形控制方程如下:

(6)

式中:G为剪切模量，MPa;ν为泊松比;εL为Langmuir体积应变;fi为弹性多孔介质体积力，MPa;α为Biot系数;pL为Langmuir压力常数,为体积应变等于0.5εL时的孔隙压力，MPa。

2.3 孔隙率方程

Zhang等[12-15]人建立普遍应用的动态孔隙度与渗透率模型。对其中孔隙率求偏导的表达式:

(7)

式中:

式中：n为孔隙率，%;εv为煤体体积应变;Ks为煤体骨架体积模量,MPa。

2.4 初始条件及边界条件

1) 初始条件:

(8)

(9)

(10)

式中:u0为煤变形场内的初始位移;σ0为煤变形场内的初始应力，MPa;p0为煤层中初始的瓦斯压力，MPa。

2) 边界条件:

(11)

(12)

(13)

式中:ui(t)为边界上的位移;fi(t)为边界上的应力;pi为煤层边界压力，MPa。

3 数值模拟结果及分析

3.1 几何模型和相关参数

瓦斯抽采二维模型模拟的工程条件为:上覆岩层为h米,巷道高为3 m,走向长60 m,钻孔位于模型的中间位置,假设四周的流量为零。选取晋城某矿作为研究对象,其主要的参数如表1所示。

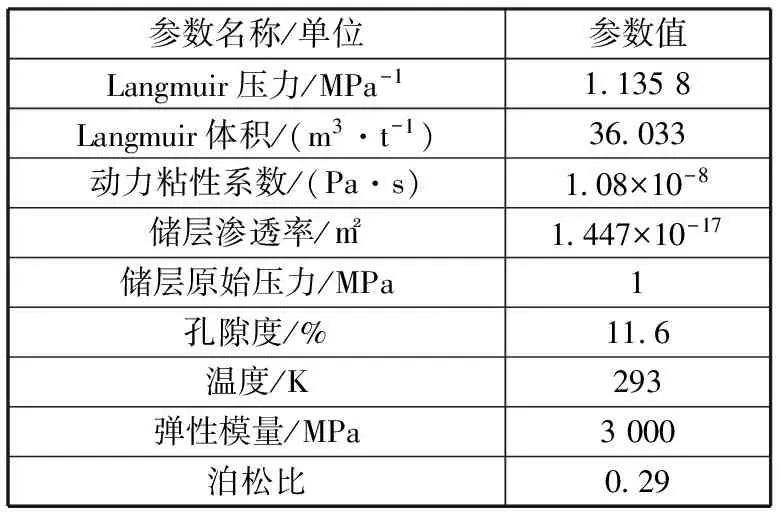
表1 主要参数表

3.2 模拟结果及分析如下:

3.2.1 抽采有效半径

为了方便对比分析,设定煤层内部瓦斯初始压力为1 MPa,抽采负压为20 kPa,应力初始位移为0。上覆岩层包括煤本身的重量所产生的压应力为7 MPa,模拟结果如图1。

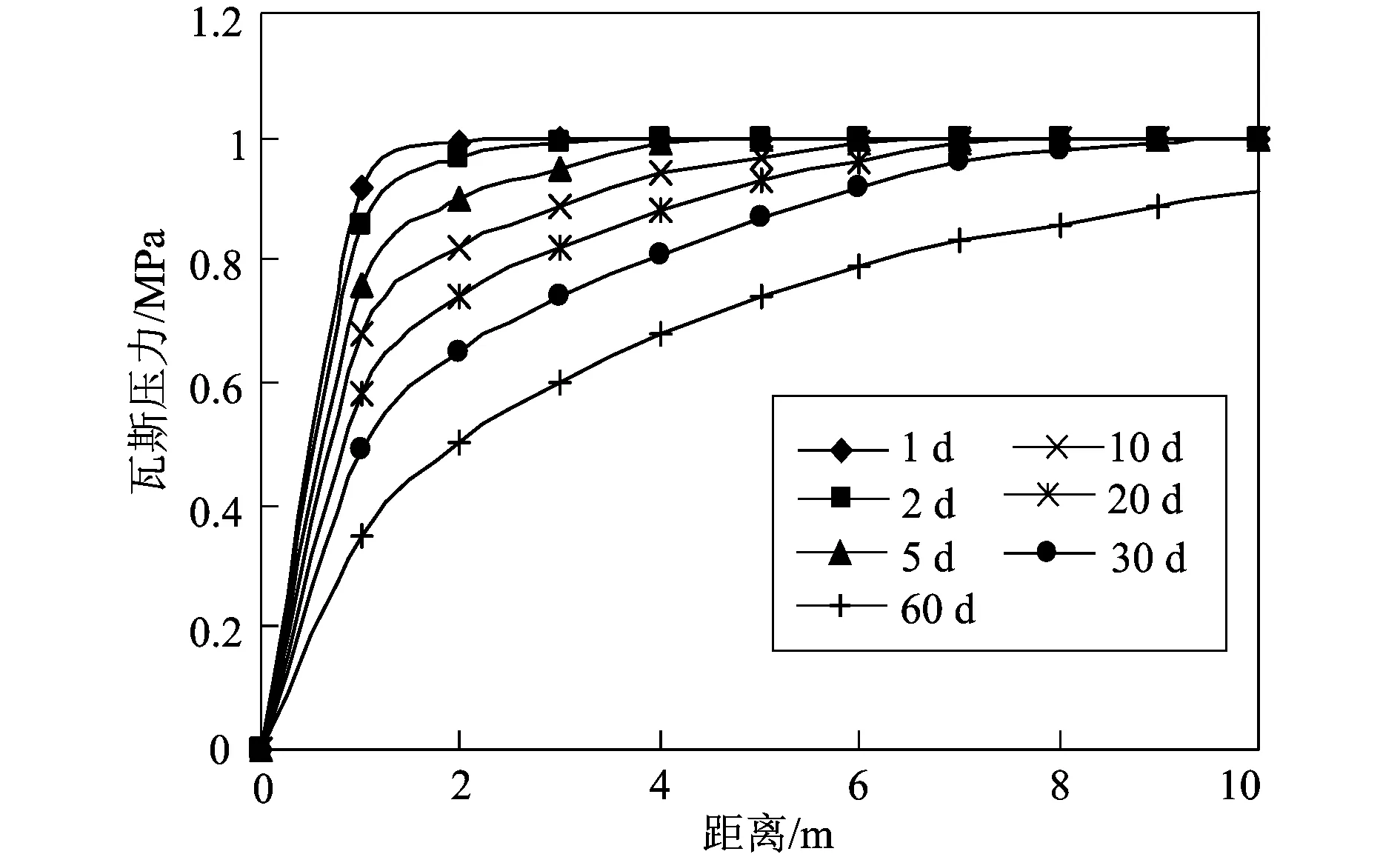
图1 钻孔垂直平面压力随距离的变化规律

预抽煤层瓦斯时,抽放钻孔周围的瓦斯在煤层原始压力及抽采负压的影响下被不断的抽采出来。在抽采的初始阶段,瓦斯压力下降较快。随着时间的延长,瓦斯压力下降逐渐减弱,瓦斯抽采影响半径逐渐扩大,当瓦斯压力下降到0.74 MPa,即残余孔隙压力时,煤层瓦斯抽采孔衰竭,此时达到瓦斯的有效抽采半径。根据模拟表2可知,抽采有效半径与抽采时间之间关系符合幂函数y=AtB,其中y瓦斯抽采有效半径;t抽采时间;A,B常数与瓦斯赋存及煤储层特征等相关参数有关。此关系式为现场的抽采时间、钻孔间距布置等瓦斯抽采工艺参数提供了一定的理论依据。

表2 不同时间下的有效抽采半径

3.2.2 上覆应力影响

煤层埋藏深度不同,所受的上覆应力不同,选取三个包括煤层自身重量的上覆岩层所产生的压应力分别为3 MPa、7 MPa、10 MPa。煤层内部瓦斯初始压力为1 MPa,抽采负压为20 kPa,应力初始位移为0。在相同时间内(t=30 d)不同上覆应力下的瓦斯压力分布如图2。

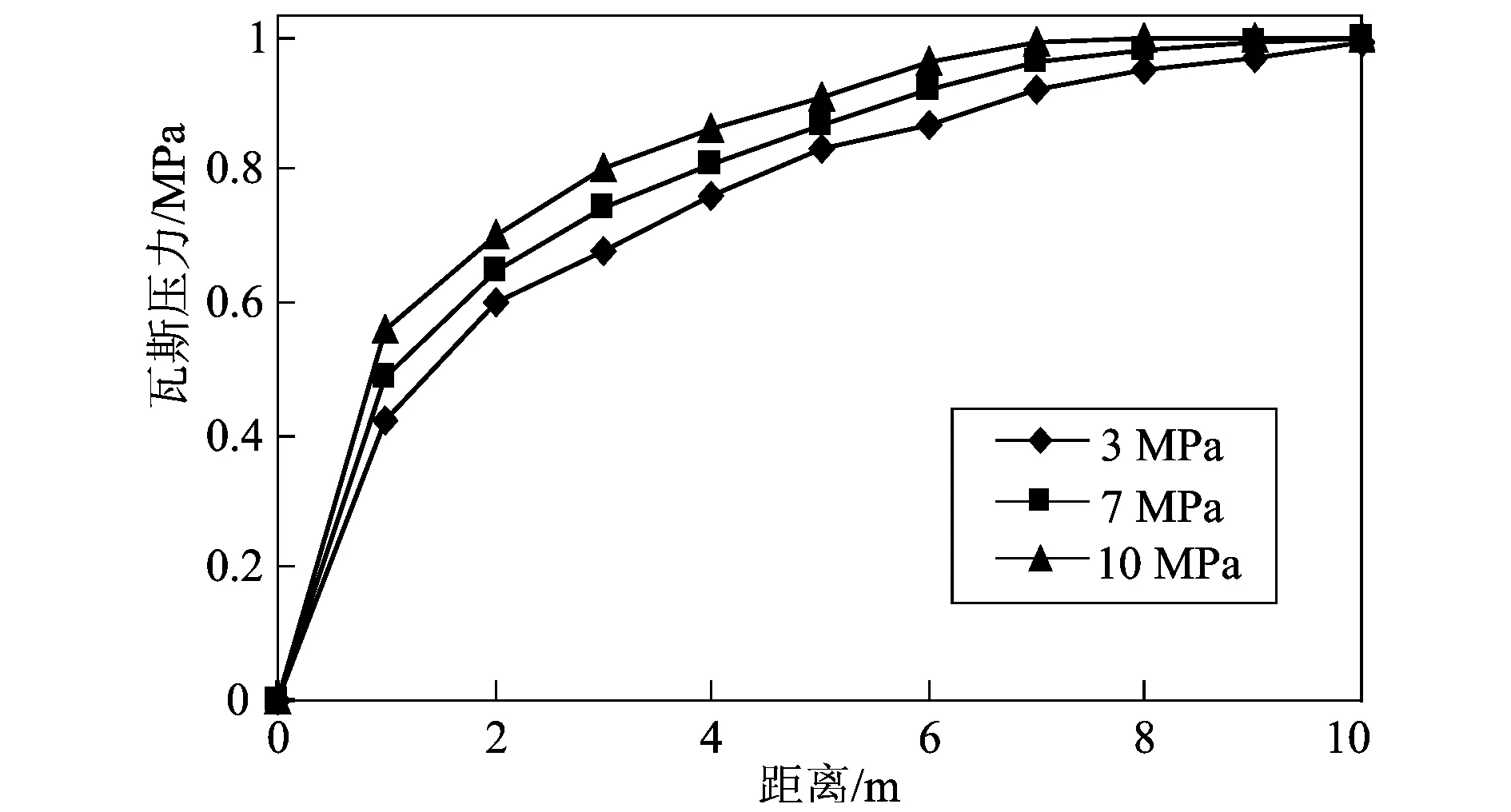
图2 不同上覆压力条件下瓦斯压力分布图

从图2分析可知,在一定的范围内,上覆压力与瓦斯抽采有效半径之间呈负相关,即上覆压力越大越不易抽采,且对于不同煤质均适应。

在煤层开采过程中,上覆压力随煤层埋藏深度的增加而增大,同时煤岩体被压缩,导致孔隙率和渗透率降低,增加了瓦斯抽采难度。根据此原理,实际中可以利用水力压裂、预裂爆破、注气等方法提高煤层的渗透率,从而增加瓦斯抽采率。

3.2.3 不同抽采负压影响

设定煤层内部瓦斯初始压力为1 MPa,应力初始位移为0。上覆岩层包括煤本身的质量所产生的压应力为7 MPa。模拟在相同时间内(t=30 d)不同的抽采负压(10，20，30 kPa)情况下的瓦斯压力分布如图3。

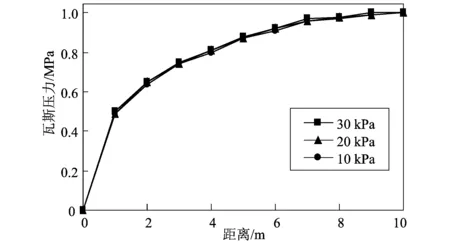
图3 不同抽采负压条件下瓦斯压力分布图

从图3可以看出,不同抽采负压条件下瓦斯压力分布几乎一致,通过进一步分析可知在不同抽采负压条件下,瓦斯抽采有效半径与抽采时间之间都符合幂函数关系,且对于不同煤质均适应。在瓦斯抽采的过程中要考虑实际情况选取合适的抽采负压,单纯依靠增大抽采负压来提高采收率的方法不能解决实际问题。

4 结论

1) 以瓦斯同步运移理论为基础,考虑瓦斯在孔隙中扩散过程,建立了瓦斯抽采气固耦合物理数学模型，该模型诠释了一种新的瓦斯运移历程。

2) 在瓦斯抽采过程中,抽采时间与抽采有效半径之间符合幂函数关系,此为瓦斯抽采工艺设计提供了一定的理论依据。

3) 利用不同开采深度,上覆应力随深度的增加而增大的结论,现场可采用有效方法提高煤层孔隙率和渗透率,从而增加瓦斯抽采率。

4) 对于不同煤质而言,在抽采过程中抽采负压的变化对瓦斯抽采率影响不大。

[1] 章梦涛,梁冰,梁栋.采动影响下煤层内瓦斯流动状况的数学模型及数学分析[M].∥第二届全国岩石力学数值计算与模型试验学术研讨会论文集,上海:同济大学出版社,1990:423-428.

[2] 司鹄,郭涛,李晓红.钻孔抽放瓦斯流固耦合分析及数值模拟[J].重庆大学学报,2011,34(11):105-110.

[3] 赵阳升.煤体-瓦斯耦合数学模型与数值解法[J].岩石力学与工程学报,1994,13(3):229-239.

[4] 梁冰,章梦涛,王泳嘉.煤层瓦斯渗流与煤体变形的耦合数学模型及数值解法[J].岩石力学与工程学报,1996,15(2):135-142.

[5] 周军平,鲜学福,姜永东.考虑基质收缩效应的煤层气应力场-渗流场耦合作用分析[J].岩土力学,2010,31(7):2317-2323.

[6] 杨天鸿,陈仕阔,朱万成,等.煤层瓦斯卸压抽放动态过程的气-固耦合模型研究[J].岩土力学,2010,31(7):2247-2252.

[7] 杨天鸿,徐涛,刘建新,等.应力-损伤-渗流耦合模型及在深部煤层瓦斯卸压实践中的应用[J].岩石力学与工程学报,2005,24(16):2900-2905.

[8] Connell L D.Coupled flow and geomechanical processes during gas production from coal seams[J].International Journal of CoalGeolo-gy,2009,79:18-28.

[9] 吴世跃.煤层气与煤层耦合运动理论及其应用的研究-具有吸附作用的气固耦合理论[M].北京：科学出版社,2009.

[10] 宋岩,柳少波,洪峰,等.中国煤层气地球化学特征及成因[J].石油学报，2012，33(1):99-106.

[11] CLARKSON C R.Adsorption potential theories to coal methane adsorption isotherms at elevated temperature and pressure[J].Carbon，1997，35:1689-1705.

[12] 孙培德.SUN模型及其应用[M].杭州:浙江大学出版社,2002.

[13] Detournay E,Cheng AHD,Fundamenta is of poroelasticity[M]∥Fairhurst C,editor.Comprehensive rockengineering,1993,2:113-117.

[14] Wang J G,Akim kabirb,Liu Jishan.Effects of non-Darcy How on the performance of coal seam gas wells[J].International Journal of Coal Geology,2012(93):62-74.

[15] Zhang Hongbin，Liu Jinshan,Elsworth D.How sorption-induced matrix deformation affects gas How in coal seams:Anew FE model[J].International Journal of Rock Mechanics &Mining Sciences,2008(45):1226-1236.

(编辑：张爱绒)

Numerical Simulation of Gas-solid Coupled Field in Gas Drainage Based on the Synchronous Migration Theory

ZHANG Meihong,WU Shiyue,NIU Yu,MENG Xiaohong

(CollegeofMiningEngineering,TaiyuanUniversityofTechnology,Taiyuan030024,China)

Considering the coal mass deformation and the change of permeability and porosity in the production process of gas drainage,this paper has established the gas-solid coupling dynamic mathematical model of gas drainage,which is based on the synchronous migration theory of coal bed gas seepage diffusion.Taking a mine in Jincheng for example,combined with the characteristics of coal seam occurrence in the mine,and with the aid of Comsol multiphysics software,this paper has carried out numerical simulation.The simulation results show that the effective radius and drainage time of gas extraction accord with the power function relationship;with the increase of embedding depth of coal seam and overburden stress,the permeability and porosity of coalbed decrease,which raises the difficulty of gas drainage.So,to improve the coal seam permeability and porosity is more important compared with to increase gas extraction rate;Suction pressure of the drainage system has little effect on gas extraction.

synchronous transfer;gas field;deformation of coal;gas extraction; numerical simulation

2014-10-10

国家科技支撑计划(2007BAK29B01);山西省科技攻关项目(2007031120-02)

张美红(1982-),女，山西太原人，博士,主要从事煤层气开采研究,(E-mail)zmh-625@163.com,(Tel)13934213864

吴世跃,教授,博导,主要从事煤层气开采研究,(E-mail)Wushiyue2000@aliyun.com

1007-9432(2015)01-0060-04

TD712.51

A

10.16355/j.cnki.issn1007-9432tyut.2015.01.012