土壤模型复杂化对输电线路杆塔接地及耐雷性能的影响

唐 波,朱建雄,黄 颖,瞿子航,葛光祖

(三峡大学 电气与新能源学院,湖北 宜昌 443002)

土壤模型复杂化对输电线路杆塔接地及耐雷性能的影响

唐 波,朱建雄,黄 颖,瞿子航,葛光祖

(三峡大学 电气与新能源学院,湖北 宜昌 443002)

传统输电线路杆塔接地工程设计均基于无限大均匀土壤电性模型,该土壤电性模型与实际土壤不符,可能造成接地设计的不准确。基于拉普拉斯方程,推导了水平双层和垂直双层土壤电性模型下的杆塔接地装置的电位函数表达式,从而提出了相应条件下接地电阻的计算方法。以三门峡地区110 kV中横线典型铁塔接地为例,分别采用规程法和分层土壤精确计算法,对无限大均匀土壤、水平双层和垂直双层等土壤电性模型下的典型线路杆塔反击跳闸率进行了计算。结果表明,若以无限大均匀土壤设计接地装置,其反击跳闸率较土壤二分层情况低。

输电线路;杆塔接地装置;接地电阻;土壤电性模型;反击跳闸率

坚强可靠是我国智能电网建设的五个主要内涵之一[1],而雷击是造成电网故障的最主要因素[2]。尽管输电线路和变电站采取了大量的防雷保护措施,以减少电网雷害事故[2],但我国每年由于雷击造成的输电线路绝缘闪络和损坏而影响电网正常运行的故障仍频繁发生。据统计,由于雷击引起的高压线路跳闸次数占线路总跳闸次数的40%～70%[3]。

输电线路杆塔接地电阻值是防雷接地系统的一项重要技术指标,是衡量接地效果的主要参数,直接影响到系统的防雷效果。文献[4-9]给出了我国输电线路工程中杆塔接地装置设计流程及其接地电阻值的工程计算方法。这些标准规范均以四极法测得的土壤电阻率为设计依据,进行相应接地装置的设计与计算。然而,土壤电阻率四极法测量的理论依据为大地视为无限大均匀土壤电性模型,这种无限大均匀土壤模型显然与实际线路杆塔周边土壤有所差别。考虑到输电线路所经地区非常复杂,由于地形地质和微气象的关系,线路杆塔周边的土壤、砂、石、泥、水的含量不同,线路勘测时各观测点得到的土壤电阻率其实上并非为一常数。因此,若单纯按照无限大均匀土壤模型进行设计,必然存在一定的土壤电阻率、接地装置电阻值及雷击跳闸率误判。

对于特高压线路来说,由于线路整体较为高大,绝缘性能较好,主要面临绕击影响;而对于普通高压线路来说,特别是位于山区的高压线路由于土壤电阻率高、地形复杂,交通不变,施工难度大,杆塔接地电阻普遍偏高,一旦杆塔遭受雷击,相邻杆塔不能有效分流,极易形成反击。本文以三门峡地区110 kV中横线68号典型铁塔为例,采用拉普拉斯方程研究土壤电性模型水平分层、垂直分层等情况下杆塔接地装置的工频接地电阻值及对应的反击跳闸率,分析相对于常规设计思想,土壤电性模型复杂化对线路杆塔接地电阻及反击跳闸率的影响水平。

1 接地电阻及其工程求解

1.1 杆塔接地电阻及其相关标准

输电杆塔接地装置是指埋设在地下的接地电极与由该接地电极到杆塔基础之间的连接导线的总称。接地电阻是电流I经接地电极流入大地时,接地电极的电位V对I的比值,其中,接地电极的电位V为接地电极与无穷远零位面之间的电位差。因此,接地电阻也可定义为由接地电极到无穷远处土壤的总电阻。良好的接地装置有利于雷电流入地,原则上要求接地装置的接地电阻越小越好。

线路设计技术规程规定[10],有电线的杆塔应接地。在雷季干燥时,每基杆塔不连地线的工频电阻,不宜大于表1的要求。

表1 有地线的杆塔工频接地电阻范围

1.2 线路工程设计中的接地电阻计算

在接地工程中所遇到的接地电极的几何形状是多种多样的,文献[11]给出了输电线路工程设计中杆塔接地电阻的详细计算流程和方法。当接地电极的形状简单而又比较规则时,可以采用一定近似后用解析法直接导出计算公式。常见的简单接地电极不外乎圆棒型、圆环型和圆盘型,这些接地电极的计算也是以后复杂接地体计算的基础。

以垂直圆棒型接地体为例,文献[11]给出了当l≫d时,垂直圆棒型的接地体的接地电阻的计算公式:

(1)

式中：ρ为土壤电阻率,Ω·m；l为接地体的长度,m;d为接地体的直径,m。

2 复杂土壤电性模型下的接地电阻数值计算

在杆塔接地电极埋设处,土壤电阻率往往是不均匀的。若按照土壤实际复杂程度进行建模,则模型非常复杂,计算极为繁琐,且准确的土壤电性分布又无法准确获取。因此,研究时通常将非均匀土壤进行分层建模计算,一般分为沿水平方向分层或沿垂直方向分层两种。文献[12-13]认为这种分层方法所造成的误差在工程允许范围,因此,本文也采用这两种分层土壤电性模型进行研究。

2.1 水平双层土壤模型中的接地电阻计算

作为土壤分层接地计算的基础,可研究最简单的双层土壤中点电流源的电流场,该问题可以用拉普拉斯方程求解。

恒定电场中的拉普拉斯方程为:

(2)

式中：φ为电位；电场强度E=-φ。考虑到场的对称性,使用圆柱坐标系O(r,θ,z),上式变为:

(3)

求解土壤的电位函数采用的是分离变量法、傅里叶变换等一些数学方法,从而拉普拉斯方程的解变为:

式中:φ(λ)和γ(λ)为待定系数;J0(λr)为第一类零阶贝塞尔函数;λ为任意常数。

由于均匀媒质中点电流源的点位函数必然满足泊松方程,则可利用傅里叶变换,结合拉普拉斯方程的解及待定系数法,推导得到上层土壤中的电位函数。建立如图1所示的坐标系统,根据文献[12]的推导,上层土壤电位函数φ1为:

(4)

式中:

下层土壤电位函数φ2与φ1求解过程完全相似。

图1 双层土壤中电流场的坐标系统

2.1.1 接地电极不穿入下层土壤时的情况

当接地电极不穿入下层土壤如图2所示,电极上端表面处的电位代表电极电位,电极的电位可直接利用拉普拉斯方程的解求出。

图2 垂直接地体不穿入下层土壤

在式(4)中令z=-h,r=a,写出电流I自棒上某一深度为h的dh元段流出时,电极上端表面处的电位:

(5)

再将上式沿棒长积分,即可得到电极的电位为:

(6)

由此可得:

(7)

式中:l为接地体的长度;a为接地的半径;h1为第一层土壤厚度;k=(ρ2-ρ1)/(ρ2+ρ1).

2.1.2 接地电极穿入下层土壤时的情况

当接地电极穿入下层土壤如图3所示,将电极分成为上层土壤和下层土壤两段分别进行计算。取上层土壤中接地棒的流散电流密度为δ1,下层土壤中接地棒的流散电流密度为δ2,则有关系式:δ1ρ1=δ2ρ2;I1+I2=δ1h1+δ2(l-h1)=I,从而可以求出δ1与δ2。

图3 垂直接地体穿入下层土壤情况

为求电流I1自上层土壤中的电极段流散时电极上端表面处的电位,可利用式(6),将其δ用δ1取代,l用h1取代即可。可得:

(8)

为求电流I2自下层土壤中的电极段流散时电极上端表面处的电位,需先由拉普拉斯方程解除电流δ2自下层土壤中某点流散时土壤中的电位函数。详细推导过程可参见文献[12]。埋设于下层土壤的电极电位函数为:

(9)

将上下两层土壤电位叠加,再将δ1与δ2分别代入,经过整理可以得到垂直接地电极穿入下层土壤时的电阻为:

(10)

2.2 垂直分层土壤模型中的接地电阻计算

垂直两层土壤中,接地电阻也可以用镜像法及拉普拉斯方程进行计算。图4给出了埋设在垂直二分层土壤时的接地电极。

接地电阻的表达式为[12]:

(11)

式中,D为垂直接地极的轴线到垂直分层面的距离。

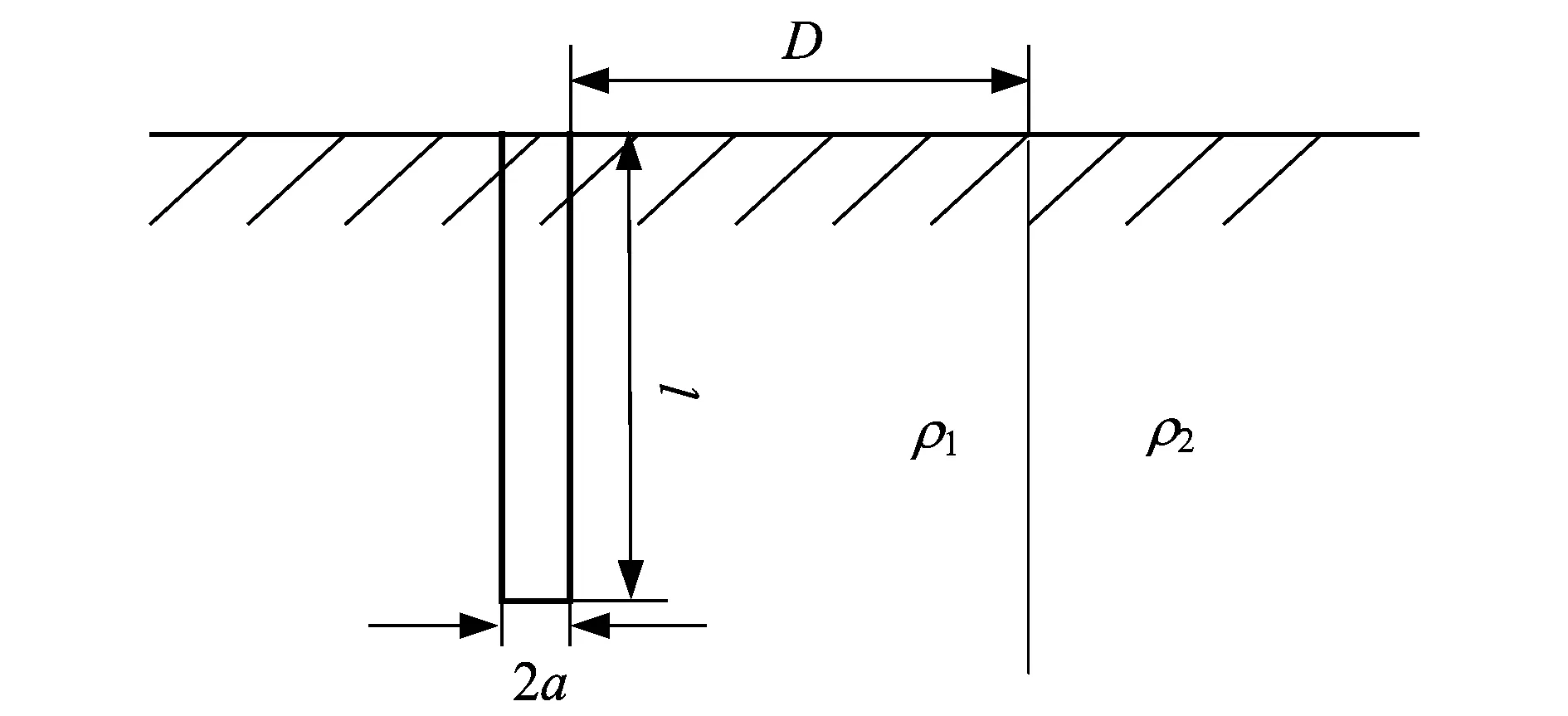
图4 垂直两层土壤中垂直接地电极

3 反击跳闸率的求解算法

反击跳闸率是指在雷暴日数Td=40的情况下、100km的线路每年因雷击杆塔后引起对导线的逆向闪络发生跳闸的次数。

依据现行电力行业规程DL/T620-1997《交流电气装置的过电压保护和绝缘配合》推荐方法,对于杆塔高度较低的输电线路的反击耐雷水平I1可由式(12)进行计算:

(12)

式中:U50%为绝缘子串50%的击穿电压;k为耦合系数;β为杆塔分流系数;ha为横担高度;ht为杆塔高;Lt为杆塔总电感;hg为避雷线对地高度;hc为导线对地高度;k0为导、地线间的几何耦合系数。

从式(12)可以看出,加强线路绝缘(即提高U50%),降低杆塔接地电阻Ri,增大耦合系数k(例如将单避雷线改为双避雷线,加装耦合地线)等,都可提高线路耐雷水平。耐雷水平增加可减小线路闪络的概率,最终减小反击跳闸率。在三相导线中,距离避雷线最远的那一相导线的耦合系数最小,一般较容易发生闪络,所以应以此作为计算条件。求得反击耐雷水平I1后,即可通过式(13)得出大于I1的雷电流出现概率P1。

(13)

按照式(14)计算反击年跳闸次数n1

(14)

式中:N为年落雷总次数;Pα为绕击率;g为击杆率;η为建弧率。

4 分层土壤电性模型对反击跳闸率的影响

以三门峡地区110 kV中横线68#典型铁塔接地装置为例,研究不同土壤电性模型下的反击跳闸率。该杆塔使用的是垂直接地体,4根塔腿的垂直接地体呈边长为s=6 m的正方形分布,垂直接地极长度l=3 m,直径2a=12 mm的圆钢。

4.1 土壤水平分层对反击跳闸率的影响

4.1.1 土壤水平分层对接地电阻的影响

均匀土壤下,土壤电阻率ρ=100 Ω·m已知,利用均匀土壤条件下垂直接地体的接地电阻计算公式(1)进行计算,则并联4根垂直接地体的接地电阻值为8.75 Ω。在土壤水平二分层情况下,假设第一层土壤电阻率ρ1=100 Ω·m,而第二层土壤电阻率ρ2=2 000 Ω·m,上层土壤厚度1。由于l≤h1,所以采用接地体不穿入下层土壤的式(6)进行计算。则并联4根垂直接地体的接地电阻值为10.34 Ω,大于规程规定的10 Ω。

从算例结果比较得出,同样的垂直接地体在考虑土壤电性模型复杂化后的接地电阻值大于均匀土壤模型下接地体的接地电阻值。特别是此算例中水平双层土壤接地电阻值已经超过杆塔接地电阻值的标准,即说明常规接地设计不安全性。

为了更好的反应不同土壤电阻率和不同长度的接地体对垂直接地电阻的影响,利用MATLAB软件编程计算当土壤电阻率ρ1=100 Ω·m,厚度h1=8 m时,在不同的k值下,一根直径2a=12 mm的不同长度的垂直接地棒的接地电阻值。当时利用式(10)计算即可。

利用MATLAB软件编程将计算结果如图5所示。同一长度的垂直接地电极阻值R随着k值的减小也就是下层土壤电阻率ρ2的减小而减小;在土壤电阻率一定的情况下,接地电阻R随着长度l的增加不断减小;当下层土壤电阻率ρ2低时,接地电极穿入到下层土壤后接地电阻值R会明显下降。

图5 水平土壤分层中不同k值下接地电阻 随接地体长度变化规律图

4.1.2 土壤水平分层对反击跳闸率的影响

三门峡地区输电线路大多位于山区[14],处于易遭受雷击的地段,为研究接地电阻对反击跳闸率的影响,取均匀土壤电阻值以及对土壤水平二分层时的接地电阻值,进行反击跳闸的计算。该地区中横线68#铁塔高15 m,铁塔的结构尺寸如图6所示。

图6 杆塔结构尺寸图,单位:m

选取4.1中的接地电阻值进行计算,耐雷水平取的三相导线中最小的。计算结果如表2。

表2 土壤水平分层下杆塔的耐雷水平

求得反击耐雷水平I1后,利用式(14)进行计算。将得到的I1值代入,可得到不同接地电阻下,超过I1的雷电流出现的概率P1值为0.184,0.162。

将计算得到的反击耐雷水平I1,超过I1的雷电流出现的概率P1代入式(15)进行计算,计算结果如表3。

表3 不同接地电阻下的反击年跳闸率

由表3可知,土壤水平二分层条件下较均匀土壤条件下反击跳闸率高,即说明常规的接地接设计是不安全的,应结合较实际的土壤电特性模型去选择合适的接地装置。

4.2 土壤垂直分层对反击跳闸率的影响

4.2.1 土壤垂直分层对接地电阻的影响

在土壤的垂直二分层情况下。假设第一层土壤电阻率ρ1=100 Ω·m;第二层土壤电阻率ρ2=2 000 Ω·m。接地装置的选取与进行水平土壤分层的所选的接地装置一致,假设接地装置有一垂直平面与土壤分层面平行。已知两平行面距离D1=5 m,易得到另外两根电极到分层面距离D2=11 m。根据土壤垂直二分层时的垂直接地电极的计算式(6)进行计算。得到并联4根垂直接的体的接地电阻为11.08 Ω。而均匀土壤的接地电阻为8.75 Ω,显然土壤垂直分层结构的接地电阻值较绝缘土壤接地电阻大。

为了更好的反应不同土壤电阻率和不同D值对垂直接地电阻的影响,利用MATLAB软件编程,计算当土壤电阻率时,垂直接地棒在不同的k值和不同D值下的接地电阻值。计算结果如图7所示。

由图7可知,同一D值下的垂直接地电极阻值R随着k值的减小也就是第二层土壤电阻率ρ2的减小而减小;当第二层土壤电阻率ρ2<ρ1,即k值小于零时,接地电阻R随着D值的增加不断增大;当第二层土壤电阻率ρ2>ρ1,即k值大于零时,接地电阻R随着D值的增加不断减小;当D=5 m时,垂直二分层土壤结构对接地电阻值的影响已经小于10%。

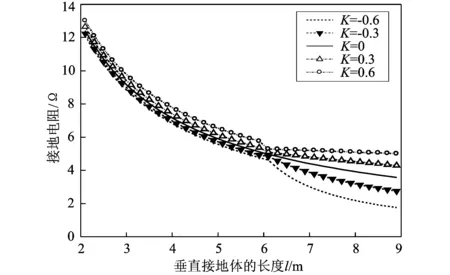
图7 垂直分层中不同k值下垂直接地 电极的接地电阻值随D值的变化曲线

4.2.2 土壤垂直分层对反击跳闸率的影响

选取的杆塔参数与求解土壤水平分层的反击跳闸率所选的杆塔参数一致,对三相导线分别进行计算,耐雷水平取三相导线中最小的,垂直土壤分层条件下计算得到杆塔的耐雷水平为62.65 kA,计算得到相应的反击跳闸率为1.147 次/年。而均匀土壤条件下杆塔的接地电阻为11.08 Ω,耐雷水平为69.67 kA,反击跳闸率为0.956 次/年。计算结果表明,垂直土壤二分层结构下,反击跳闸率会随着接地电阻值的增加而增加,所以土壤分层会使反击跳闸率的预测值偏高。而工程接地电阻设计中按无限大均匀土壤进行设计,属设计不安全。

5 结论

1)对土壤进行水平分层,当ρ1≤ρ2时,接地电阻值将大于视土壤为无限大均匀土壤的情况,杆塔反击跳闸率会随着接地电阻的增大而增大;而当ρ1>ρ2时,结论相反。

2)对土壤进行垂直分层,当ρ1≤ρ2时,接地电阻将大于将土壤视为无限大均匀土壤的情况,杆塔反击跳闸率会随着接地电阻的增大而增大;而当时,结论相反。

3)土壤结构复杂化会使接地电阻值发生改变,并引起反击跳闸率的判断出现偏差,即若按传统输电线路杆塔接地工程基于无限大均匀土壤电性模型进行接地设计,可能造成接地设计的不准确。

[1] 刘振亚.特高压电网[M].北京:中国经济出版社,2006.

[2] 胡毅.输电线路运行故障的分析与防治[J].高电压技术,2007,33 (3):1-8.

[3] 易辉.崔江流.我国输电线路运行现状及防雷保护[J].高电压技术,2001,27(6):44-45.

[4] 张波,赵杰,曾嵘,等.直流大地运行时交流系统直流电流分布的预测方法[J].中国电机工程学报,2006,26(13):84-88.

[5] 吴建标.架空线路杆塔接地的设计要点[J].电气技术,2007,(5)66-67.

[6] 王洪泽.复合接地网接地电阻的简化计算[J].电网技术,2001,25(8):70-72.

[7] 中华人民共和国信息产业部.YD 5098-2005通信局(站)防雷接地工程设计规范[S].北京:北京邮电大学出版社,2006.

[8] Sima Wenxia,Li Xiaoli,Yuan Tao.Analysis of grounding grid impulse characteristics in frequency domain in consideration of soil non-linear characteristic[J].Proceedings of the CSEE,2009,29(16):127-132.

[9] Chow Y L,Salama M M.A simplified method for calculating the substation grounding grid resistance[J].IEEE Transaction on Power Delivery,1994,9(2):736-742.

[10] 中华人民共和国国家经济贸易委员会.DL/T 5092-1999 110～500 kV架空送电线路设计技术规程[S].北京:中国电力出版社,1999.

[11] 解广润.电力系统接地技术[M].北京：水利电力出版社,1991.

[12] Ma J,Dawalibi F P,Southey R D.On the equivalence of uniform and two-layer soils to multilayer soils in the analysis of grounding systems[J].IEE Proc-Gener Transm Distrib,1996,143(1):49-55.

[13] 高廷庆,曾嵘,何金良,等.双层土壤结构的简化分析[J].清华大学学报(自然科学报),2002,42(3):349-352.

[14] 谭琼,李景禄,李志强,等.山区电网防雷技术 [M].北京:中国水利水电出版社,2011.

(编辑：刘笑达)

Influence on Power Tower Grounding and Lightning Performance of Power Transmission Line for the Complexity Soil Model

TANG Bo,ZHU Jianxiong,HUANG Ying,QU Zihang,GE Guangzu

(CollegeofElectronicEngineering&NewEnergy,ChinaThreeGorgesUniversity,Yichang443002,China)

In the traditional design of tower ground engineering of power transmission line,the soil is simulated as infinite uniform electric soil model,which is different from the actual soil.Therefore,there would be errors for ground design.Based on Laplace Equation,the potential function of tower grounding device under the horizontal and vertical two-layer soil model is deduced.As a result,the corresponding method for grounding resistance calculation is acquired.With the typical ground device of 110 kV Zhongheng power line as an example,the rules method and the accurate calculation method for layer soil model are adopted,and then the counterattack trip rates of the typical line are calculated with several of electrical models:the infinite uniform soil,the horizontal and vertical two-layer electric soil.The results show that with an infinite uniform soil for design of grounding device,counterattack trip rate is lower than those two-layer soil model.

transmission line;tower grounding device;ground resistance;electric soil model;counterattack trip rate

2014-04-05

三门峡供电公司资助项目：三门峡周边小区110 kV杆塔接地电阻特性分析及降阻措施研究(SDHZ2012087)

唐波(1978-)，男，湖北安陆人，副教授，博士，主要从事输变电系统电磁环境与超特高压输电技术研究，(Tel)13997708296

1007-9432(2015)01-0094-06

TM723

A

10.16355/j.cnki.issn1007-9432tyut.2015.01.019