注热井周围煤体蠕变过程的渗透率变化规律模拟研究

陆红波，吕兆兴，冯增朝

(1.太原理工大学采矿工艺研究所，山西 太原 030024；2.太原理工大学原位改性采矿教育部重点实验室，山西 太原 030024)

0 引 言

煤体中瓦斯的渗流不仅受到了外部条件的影响(应力和温度)，还与其自身孔隙裂隙结构有关，而且这些影响因素又相互耦合，使得对煤体瓦斯渗流的研究变得非常困难。在中国，有三分之二以上煤层的渗透性能都非常低，瓦斯不易被抽采，导致瓦斯成为开采煤矿的重大隐患。

目前，提高煤层瓦斯渗透量和渗透速率的方法大多基于以下两个思路：①通过加热、加压和水力割缝的方法改造煤体内部的孔隙、裂隙结构，增大煤体的孔隙率，最终使得煤体渗透率变大[1-2]；②通过升温、外加电磁场促进瓦斯(吸附状态)解吸或者通过注入氮气、二氧化碳和蒸汽改变瓦斯与煤体之间的亲和力(使吸附状态的瓦斯被驱替出来)，煤体中的游离瓦斯气体增加，进一步提高煤层瓦斯渗透率[3-4]。

关于煤体渗透性的研究主要是针对多物理场(热-固-流)耦合作用下煤体瓦斯运移规律研究，即在不同应力和温度的作用下对含瓦斯煤体的渗透性的影响[5-6]。然而，应力场对含瓦斯煤体渗透率影响的研究大多都假设煤体是一个线弹性体，即煤体变形是在短时间内完成的(不考虑煤体变形随时间变化)，这与煤体是一个黏弹性体的实际情况不符(煤体在长时间的应力作用下可能会产生较大的蠕变变形)，而在温度场的作用下这种蠕变变形会更加显著，因此，在研究不同应力和温度作用对于煤体渗透性的影响时，考虑煤体蠕变的影响十分必要的。

许江等[7]以型煤作为试验对象，通过对试样使用三轴压缩蠕变的手段，并在这一过程中进行了相关的瓦斯渗流试验，得到了在温度和应力不变状态下煤体蠕变前后的渗透率变化。但是实验中只是简单测量煤样蠕变前后的数据，通过公式计算出蠕变前后的型煤试样渗透率，并没有揭示出型煤试样在蠕变过程中其渗透率的演变规律。ZHU等[8]用原煤试样做实验，采用逐级加载的方式，得到了煤样在不同压力作用下其蠕变过程中的体积应变变化和渗透率变化规律。但是上述实验研究是在常温状态下研究煤体蠕变对于渗透率的影响，并没有考虑温度对于煤体蠕变和渗透率的影响。

本文针对煤体在注热和固定围压状态下，通过数值模拟的方法，研究了煤体的蠕变情况和煤体渗透率变化，为注热开采煤层气提供技术支持和参考。

1 煤体蠕变-渗流规律数学模型

为了更好地建立煤体耦合运动的数学物理方程,做了一些简化假设：连续性假设、小变形假设、各相同性假设、在耦合运动过程中煤层及其内部的瓦斯气体温度不产生变化。

1.1 注热温度场方程

煤体中的温度场方程可以由线性抛物线方程来表示，计算见式(1)。

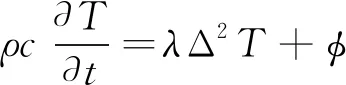
(1)

在原始煤田中进行竖井注热，可以采用第三类边界条件，计算见式(2)。

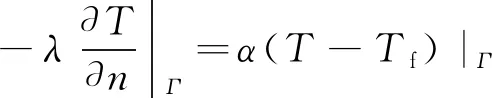
(2)

初始条件就是煤层的初始温度，计算见式(3)。

T|t=0=φ(x,y,z)

(3)

式中：ρ为煤层的均匀密度，kg/m3；c是煤体的比热容，J/(kg·K)；T是煤层的平均温度，K；λ为煤体的均匀导热系数，W/(m·K)；φ为煤体内的热源；Tf为游离态瓦斯气体的温度，℃；α是不同介质间的换热系数，W/(m·K)。

1.2 煤体变形场方程

煤体变形场方程主要包括静力平衡方程、变形协调方程、煤体蠕变本构方程。

静力平衡方程，计算见式(4)。

(4)

几何方程，计算见式(5)。

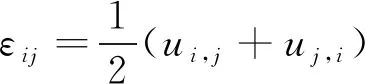
(5)

考虑温度后，煤体蠕变本构方程[12]见式(6)。

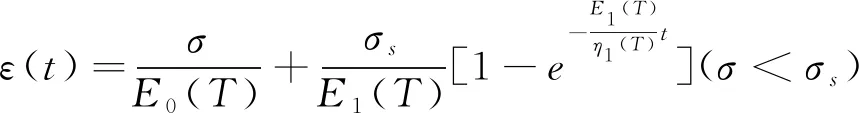
(6)

煤体的三维蠕变本构方程，计算见式(7)。

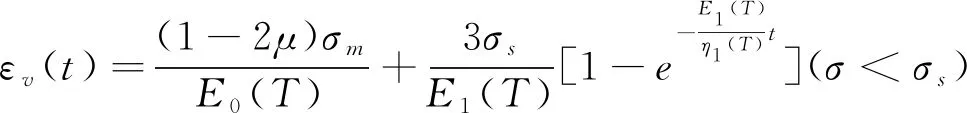
(7)

式中：G为煤体的平均剪切模量，GPa；ui,jj,uj,ji为煤体相关的位移矢量；ν为煤体的平均泊松比；F为煤体重力；P为煤体内瓦斯气体压力，Pa；α为煤体的Biot系数，0≤α≤1；K为煤体的平均体积模量，GPa；αT为煤体的均匀热膨胀系数；T,i为煤体内部的温度，K；E0(T)、E1(T)为受温度影响的弹性模量，GPa；η1、η2为不同蠕变阶段的黏性系数；σs为塑性元件阈值。

1.3 煤体渗流场方程

裂隙中气相质量守恒方程[13]见式(8)和式(9)。

(8)

(9)

式中：C为煤体的吸附瓦斯总量，kg/m3；a为煤体的饱和吸附瓦斯量；b为煤体的吸附常数；P1、Pn分别为初始吸附平衡压力和最终吸附平衡压力，Pa；D为煤体内部相关扩散系数，m/s2；q为质量源。

耦合运动微分方程，计算见式(10)。

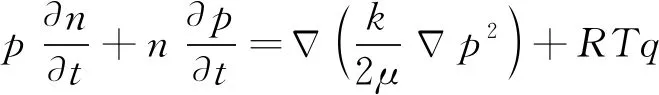
(10)

式中，p为吸附平衡压力，Pa。

吸附变形方程、孔隙率及渗透率方程，计算见式(11)～(14)。

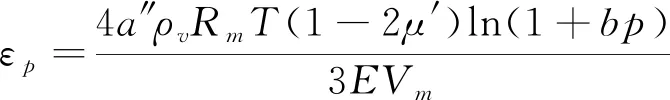
(11)

n=n0-εv-εp

(12)

(13)

(14)

式中：n、n0为煤体的均匀孔隙率和初始均匀孔隙率；εv、εp为煤体的体积应变和吸附变形；k、k0为煤体的均匀渗透率和初始均匀渗透率，m2；μ为瓦斯气体的黏度；R为煤体的气体常数。

将式(7)～(11)和式(14)代入式(10)，得式(15)。

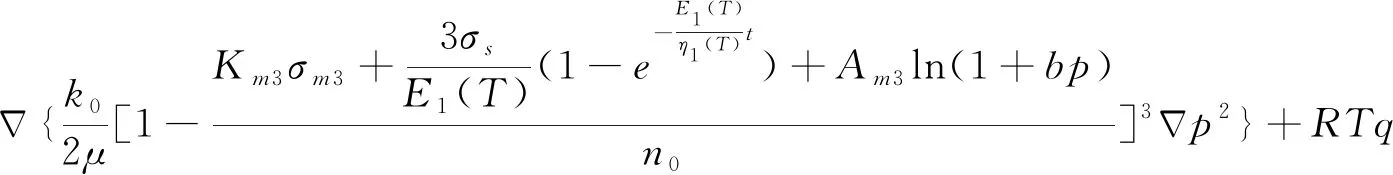
(15)

化简之后，可得式(16)。

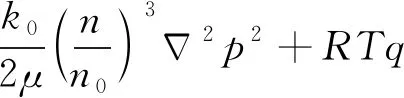
(16)

式中：Km3为煤体的平均体积模量的倒数，Pa-1；σm3为总应力单独作用下，应力重新平衡过后三维应力的平均值，Pa；Am3为煤体吸附变形的相关常数。

通过物理试验和数据处理，得到在5 MPa轴压和围压状态下，煤体的弹性模量、黏性系数与温度变化的关系，如图1所示。

煤体相关力学参数关于温度的拟合函数，弹性模量E0计算见式(17)，弹性模量E1计算见式(18)，黏性系数η计算见式(19)。

E0(T)=3×10-5T2-0.010 5T+3.5

(17)

E1(T)=22.747-0.054 9T

(18)

η(T)=6 275.7-22.23T

(19)

图1 5 MPa轴压围压、不同温度作用下煤体的弹性模量和黏性系数变化

Fig.1 Variation of elastic modulus and viscosity coefficient of coal under 5 MPa axial compression confining pressure and different temperature

2 注热煤体蠕变过程中渗透率变化规律数值模拟

使用comsol软件，分别对等温煤体和注热煤体的蠕变过程进行数值模拟，能够更加细致地得到不同温度状态下煤体蠕变过程中的渗透率变化规律。

2.1 等温状态煤体蠕变过程中瓦斯渗流数值模拟

煤体模型的尺寸为30 m×30 m×10 m，注热井半径为0.1 m。煤体模型的网格划分是采用有限元网格划分的方式，以四面体四节点对该模型进行划分，具体见图2。

温度条件：初始煤体温度为293 K，最高温度为473 K，温度步长为60 K，具体参数见表1。

围岩条件：煤体模型的正X轴、Y轴方向上有5 MPa的围岩压力，正Z轴方向上有5 MPa的上覆岩层压力，其他三个方向上为辊轴支撑作用。

渗流条件：煤体的正X方向、Y方向和负X方向、Y方向上的四个面上存在1 MPa的渗流压力，注热井筒内壁为渗流出口，煤体模型其他面不能渗流。

在轴压为5 MPa、温度为353 K、413 K和473 K的作用下，煤体蠕变过程中的体积应变、孔隙率和渗透率变化状况(考虑温度对于煤体的弹性模量和黏滞性系数的影响)，如图3～5所示。

1) 煤体在0 h时的孔隙率、渗透率，比表1中的初始孔隙率、渗透率数值小。这是由于煤体在受压过程中存在瞬时弹性应变(即初始体积应变)，煤体内部的有效渗流孔隙空间被压缩。

2) 如图6所示，煤体的初始体积应变随着温度的升高而减少，虽然温度升高导致了煤体的“软化”(即煤体弹性模量的降低)[14]，但是在较高温度作用下煤体受热热膨胀的影响大于弹性模量减小的影响。

3) 如图7所示，煤体蠕变100 h后，高温状态下的煤体体积应变较大。温度的升高会使煤体的蠕变变形增大、煤体的渗透率损失率变大。

图2 煤体注热井模型网格划分

Fig.2 Coal injection well model meshing

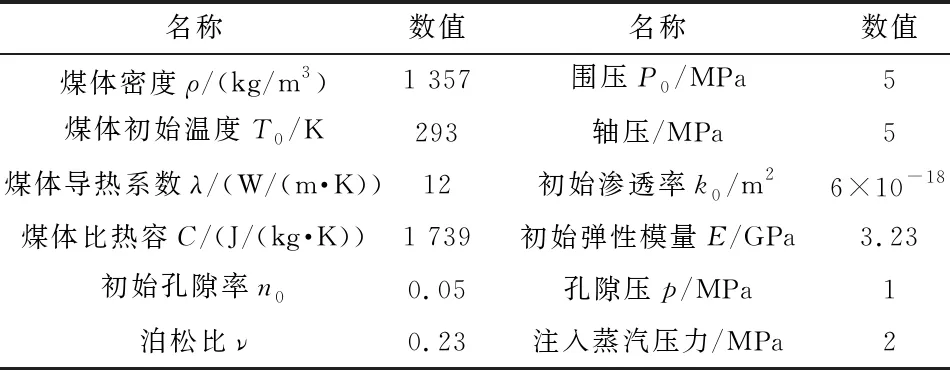
表1 煤体的相关参数

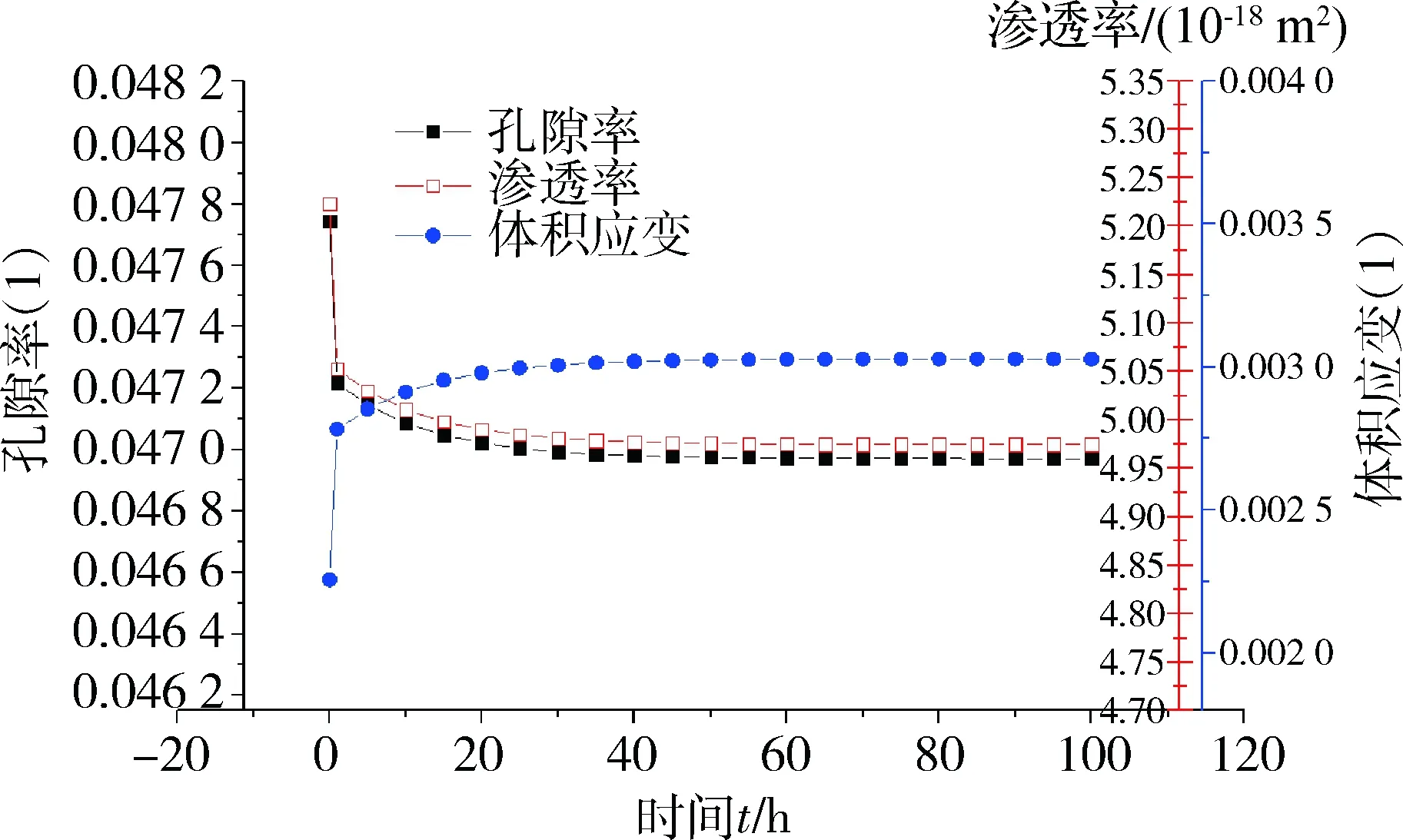
图3 5 MPa轴向应力、353 K温度作用下煤体的体积应变、孔隙率及渗透率变化

Fig.3 Variation of volumetric strain,porosity and permeability of coal under axial stress of 5 MPa and temperature of 353 K

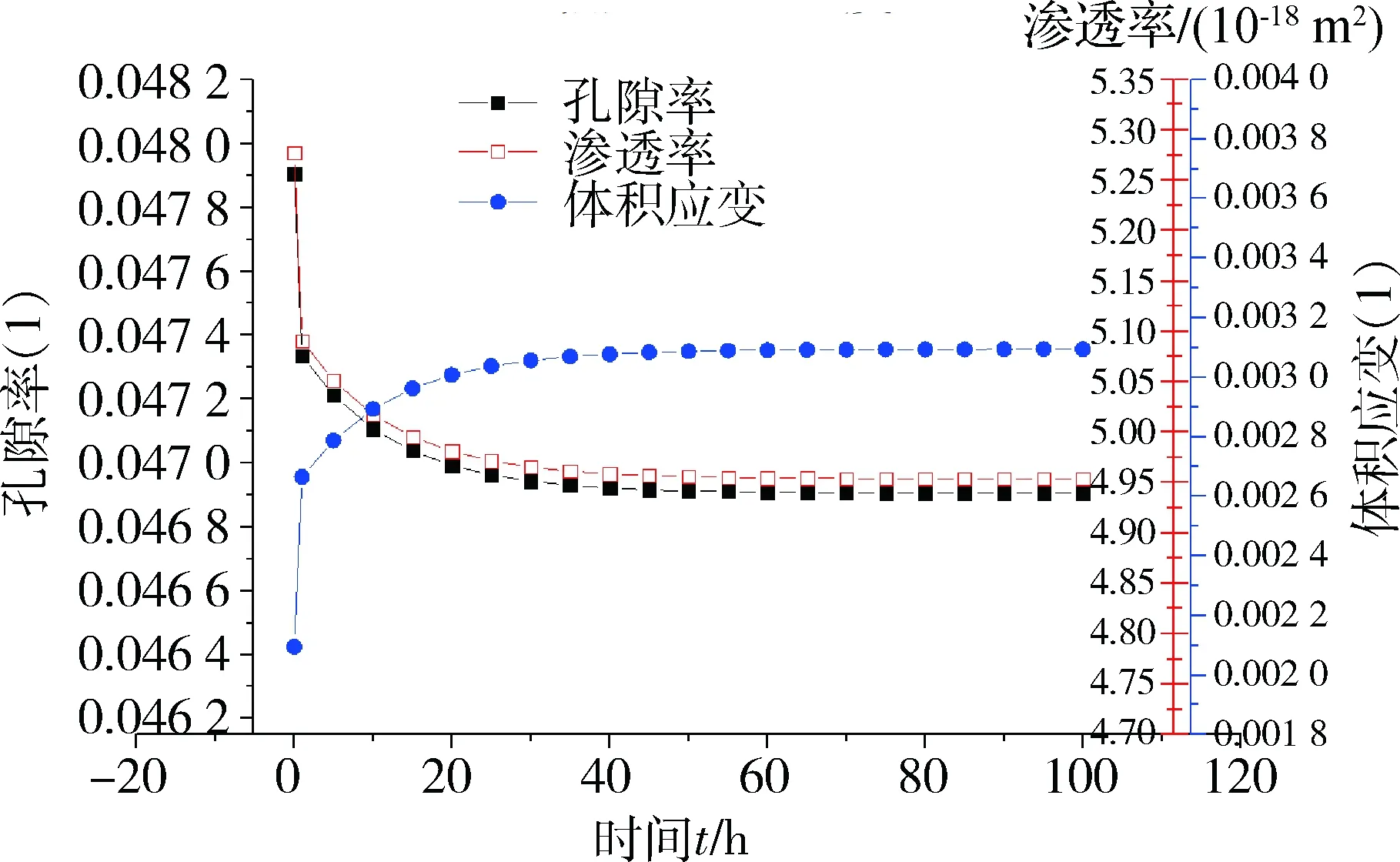
图4 5 MPa轴向应力、413 K温度作用下煤体的体积应变、孔隙率及渗透率变化

Fig.4 Variation of volumetric strain,porosity and permeability of coal under axial stress of 5 MPa and temperature of 413 K

图5 5 MPa轴向应力、473 K温度作用下煤体的体积应变、孔隙率及渗透率变化

Fig.5 Variation of volumetric strain,porosity and permeability of coal under axial stress of 5 MPa and temperature of 473 K

图6 5 MPa轴向应力、不同温度作用下煤体的初始体积应变、孔隙率及渗透率

Fig.6 Initial stress strain,porosity and permeability of coal body under axial stress of 5 MPa and different temperatures

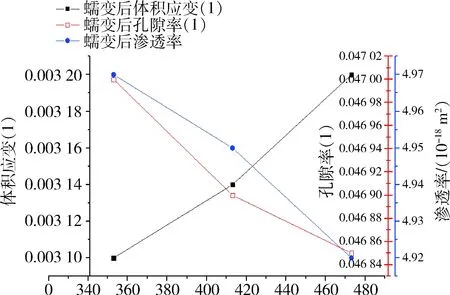
图7 5 MPa轴向应力、不同温度作用下煤体蠕变100 h时的体积应变、孔隙率及渗透率

Fig.7 Volumetric strain,porosity and permeability of coal body under 5 MPa axial stress and creep at 100 h

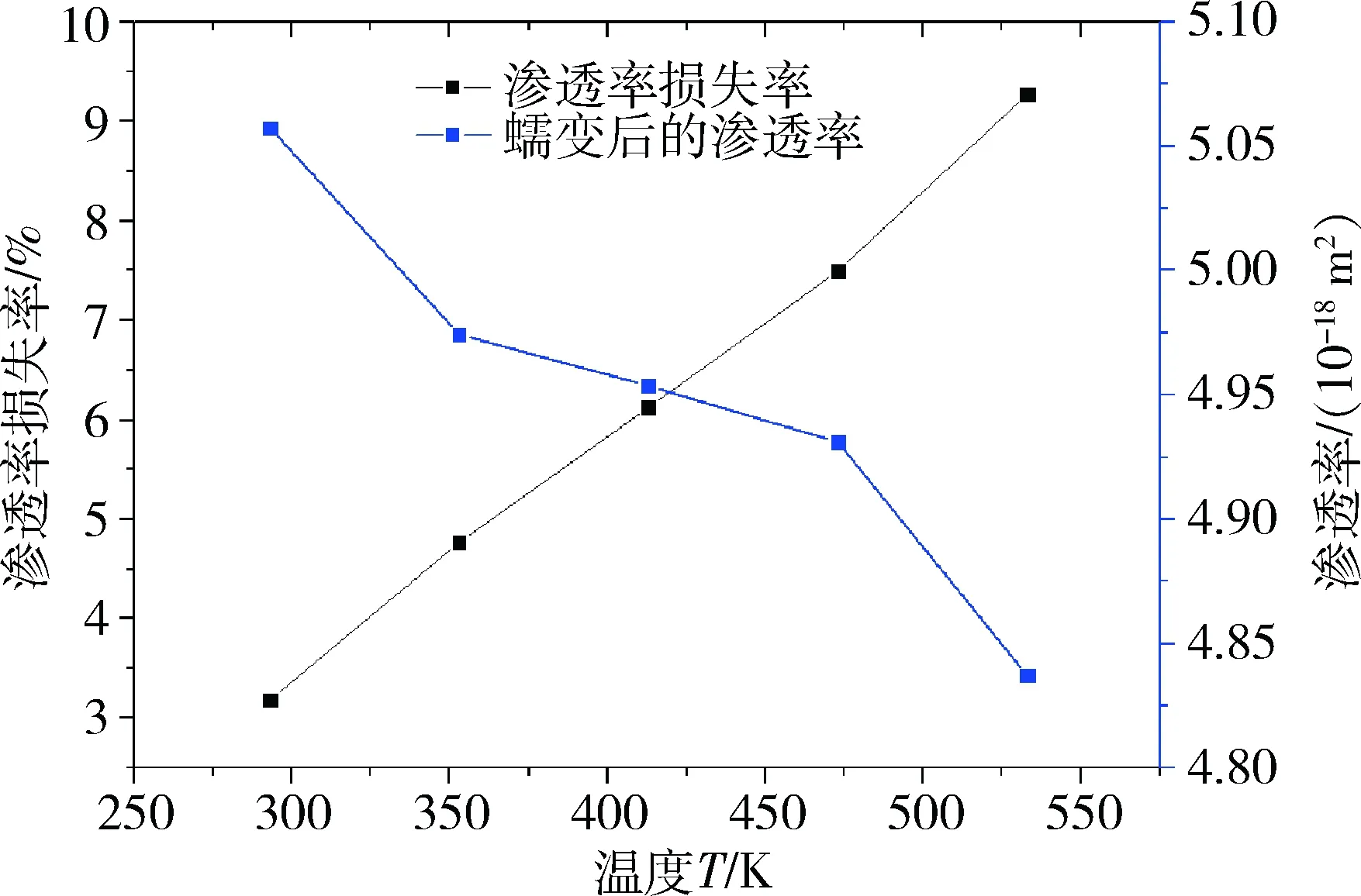
图8 不同温度状态下煤体蠕变后的渗透率变化和渗透率损失状况

Fig.8 Permeability change and permeability loss after creep of coal under different temperature

总的来说，温度升高对煤体内部瓦斯渗流作用有利有弊。①从图8中可以看出，在考虑煤体蠕变的状况下，温度升高，最终出现煤体渗透率下降的现象，其渗透率的损失率也在增加；②因为煤体温度升高，可能会促使其内部的瓦斯解吸，使煤体内瓦斯气体含量增加，也使瓦斯分子的动能变大，使瓦斯渗流速度变大。

2.2 注热后煤体温度、孔隙率以及渗透率的分布变化情况

温度条件：煤体的注热井壁温度设定为固定值573 K，使用多孔介质传热模型，煤体模型的其他面均不能传热，注热时间为20 d；其他条件与上节的相同。在注热过程中，煤体整体的温度情况。

为了进一步研究非等温对煤体蠕变及煤体渗透率的影响，选取距离注热井井壁0.5 m和2 m的任意两点导出其温度、孔隙率和渗透率数据，可以较为直观地看出煤体蠕变和渗透率变化趋势(图9和图10)。

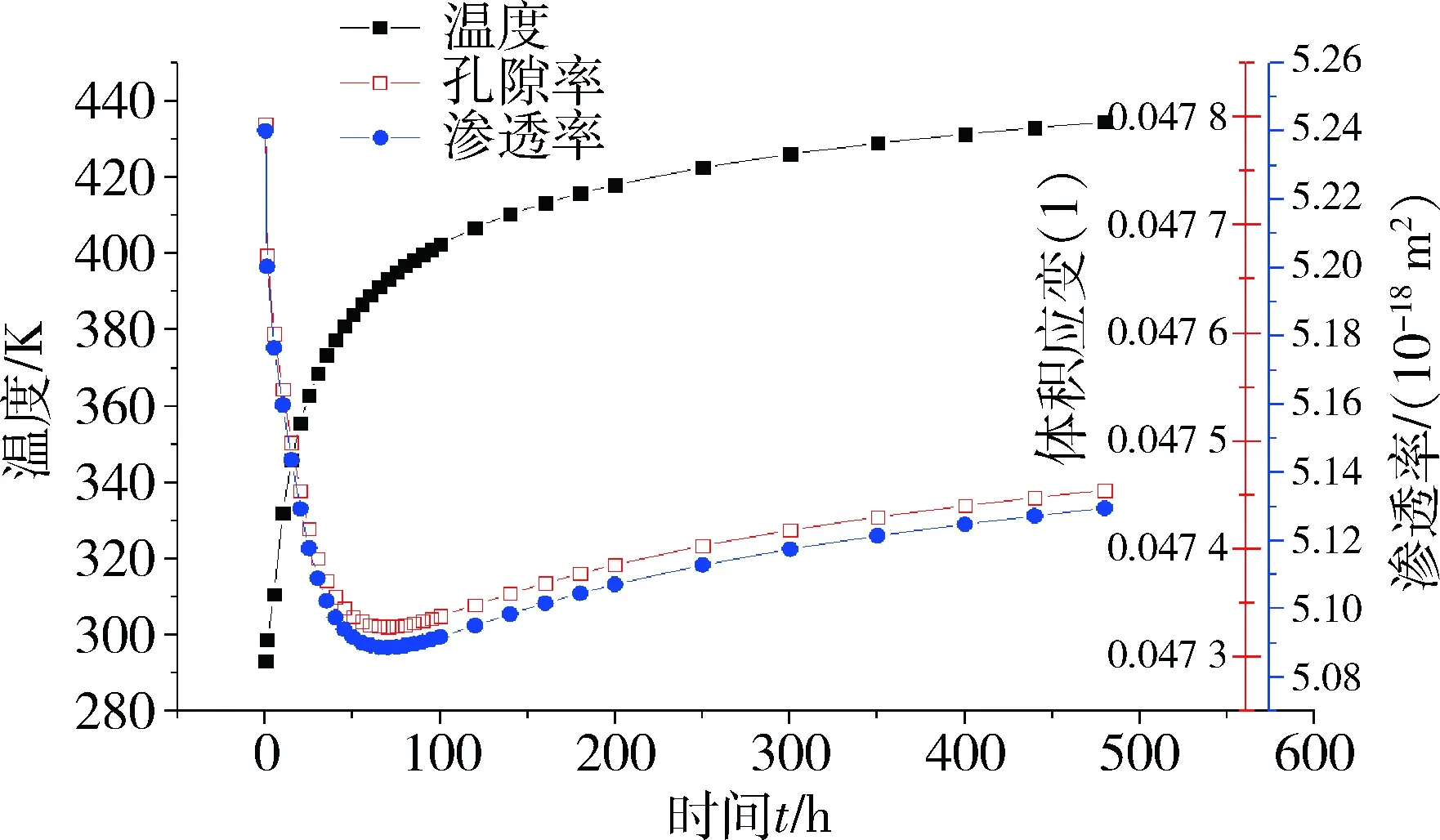
图9 5 MPa轴向压力、573 K注热温度、距离井壁0.5 m处点的温度、孔隙率和渗透率变化

Fig.9 Temperature,porosity and permeability change at a point 0.5 m away from the borehole wall under axial stress of 5 MPa and injection temperature of 573 K

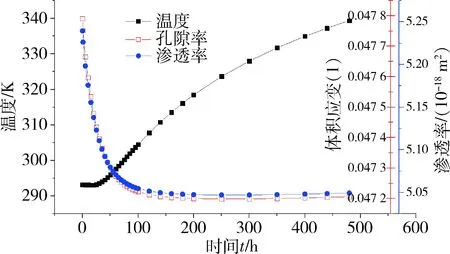
图10 5 MPa轴向压力、573 K注热温度、距离井壁2 m处点的温度、孔隙率和渗透率变化

Fig.10 Temperature,porosity and permeability change at a point 2 m away from the borehole wall under axial stress of 5 MPa and injection temperature of 573 K

1) 注热初期，距离注热井壁较近区域的温度梯度较大，井壁周围区域升温较快；注热后期其井壁周围的温度梯度减小，温度的增长速度明显下降直至最后煤体温度趋于稳定。

2) 距离注热井壁2 m处的点，其前期温度梯度较小，升温速度不明显。当距离井壁更近的区域温度迅速升高，导致该点的温度梯度增大，从而使得这一点的温度也迅速升高。

3) 因为煤体存在一个温度阈值，约为383 K。在图9中，当该点的温度小于阈值383 K时，煤体因升温而使弹性模量减小的影响较大，所以在该时间段内煤体的孔隙率和渗透率减少；当该点温度大于阈值383 K时，煤体因升温而产生热膨胀的影响较大，该点的孔隙率和渗透率上升。

4) 而在图10中，该点的温度小于阈值383 K，随着注热时间增加，煤体体积应变和渗透率并无明显回升。煤体温度升高，会使其弹性模量减小、黏性系数变大，进一步导致煤体的蠕变变形程度，煤体有效孔隙率减小，其渗透率也呈减小趋势。

3 结 论

1) 煤体温度升高，会使得其弹性模量减小，黏性系数变大，这就增大了煤体蠕变变形程度，最终使得煤体蠕变过程中渗透性能呈明显的下降趋势。

2) 注热井周围区域的升温快慢与温度梯度存在联系：越靠近注热井壁的煤体，因为其温度梯度较大，所以升温也较快；距离注热井壁较远的煤体初始温度比较低，其温度梯度也比较小，则升温较为缓慢。

3) 在注热井的持续注热过程中，煤体的高温区域内，其煤体骨架受热向外膨胀，“抑制”了注热周围的压缩变形，该区域内的煤体体积应变数值变大，所以其渗透率会因其温度升高而呈现变大的状况。

4) 煤体温度在未达到阈值383 K前，其温度的升高，会使煤体渗透率减少：在超过阈值后，煤体温度升高，会致使其渗透率增大。

5) 煤体在注热20 d后，其高温区域还是较小，而且其余区域的煤体温度提升较小。注热增产煤层气技术的经济成本可能比较高；如果考虑煤体因温度升高而蠕变变形程度加剧，可能该项技术的实际生产效果会有所降低。