基于复杂网络视角的航空通信网络鲁棒性分析

2015-06-19张凤鸣吴虎胜

系统工程与电子技术 2015年1期

关键词：级联鲁棒性攻击者

张超，张凤鸣，王瑛，吴虎胜

（1．空军工程大学装备管理与安全工程学院，陕西西安710051；2．武警工程大学装备工程学院，陕西西安710086）

基于复杂网络视角的航空通信网络鲁棒性分析

张超1，张凤鸣1，王瑛1，吴虎胜2

（1．空军工程大学装备管理与安全工程学院，陕西西安710051；2．武警工程大学装备工程学院，陕西西安710086）

针对军事航空通信网络会遭敌攻击的实际情况，引入了一种不完全信息条件下的复杂网络攻击模型，分析了该模型在航空通信网络上的级联失效原理，并给出了航空通信网络的鲁棒性度量方法。最后，通过设置不同的不完全信息攻击模型参数和级联失效参数，对航空通信网络鲁棒性进行了仿真分析，验证了所提方法的可行性和有效性。

复杂网络；航空通信网络；鲁棒性；不完全信息；级联失效

0 引言

航空电子系统作为空中作战平台火控、显控、制导、导航、通信、电子对抗等先进电子装备的集成平台，是现代空中作战平台的“中枢神经”，在很大程度上决定着平台的作战效能。随着电子技术和通信技术的不断发展，空中作战平台之间的军事航空通信网络（以下简称航空通信网络）也得到了长足进步，性能不断提升。在未来分布式网络化的空中战场中，航空通信网络将广域分散的空中作战平台连成了一个整体［1］，为空中作战平台实施协同作战奠定了基础。

航空通信网络在敌我对抗中可能遭受外部攻击，其内部系统也可能出现故障，航空通信网络能否在人为破坏、随机性破坏和部件失效时保障空中作战平台之间的信息交互和协同作战，即航空通信网络的鲁棒性问题，成为军事领域研究的热点。航空通信网络的鲁棒性是决定整个空中作战体系协作威力发挥的重要因素之一，具有十分重大的研究意义。复杂网络作为观察系统复杂性的全新视角和有力工具，已广泛应用于基础通信、作战指挥、后装保障等军事领域［23］，而鲁棒性正是复杂网络研究的核心问题之一。许多学者从不同角度研究了军事领域复杂网络的鲁棒性，如文献［4］对保障网络系统的结构和要素进行了分析，提出了提高网络系统可靠性和抗毁性的方法；文献［5］探讨了多层结构的舰艇编队作战系统的鲁棒性；文献［6］考察了随机攻击和蓄意攻击对指挥控制系统鲁棒性的影响。此外，还有一些对一般复杂网络鲁棒性和级联失效的研究［7-14］，其中，文献［7］比较了随机攻击和蓄意攻击对不同网络结构的影响，该研究表明对于随机攻击，无标度网络的抗毁性比随机网络强，而对于蓄意攻击，无标度网络则十分脆弱。

本文将空中作战平台抽象成节点、将平台之间的信息交互关系抽象成边，运用复杂网络模型，对航空通信网络的鲁棒性进行研究。考虑“战争迷雾”对敌方攻击策略的影响，引入一种不完全信息条件下的攻击策略，并考虑级联失效对航空通信网络鲁棒性的影响，设计航空通信网络级联失效模型，最后给出航空通信网络鲁棒性的度量方法。

1 航空通信网络建模

节点vi表示空中作战体系内的各种作战实体，作战实体可以描述为各种空中作战平台，集合V＝｛v1，v2，…，vN｝为所有作战实体的集合，其数量为N＝|V|。

边ej表示作战实体之间的通信连接关系，若两个作战实体存在通信链路，则认为这两个节点有边相连，否则无边。由于航空通信网络中任意两个作战实体之间的通信具有双向性，因此本文所建立的航空通信网络模型为无向网络，并且任意两个作战实体之间最多存在一条边相连。集合E＝｛e1，e2，…，eM｝为航空通信网络中所有连接关系的集合，其数量为M＝|E|。

点权值pvi表示航空通信网络中单个作战实体的通信工作属性，如：作战实体的通信容量。点权集为Pv＝｛pv1，pv2，…，pvN｝。

边权值pej表示航空通信网络作战实体间通信链路的属性，如：通信时延、通信带宽、通信量等。边权集为Pe＝｛pe1，pe2，…，peM｝。

在本文研究中，用作战实体的通信容量表征点权值pvi，用作战实体之间的通信时延表征边权值pej。

2 不完全信息条件下的攻击策略

航空通信网络面临的攻击模式一般可以分为随机攻击和蓄意攻击（选择性攻击）两种样式。对于攻击者来说，随机攻击和蓄意攻击实质上是两种极端的攻击模式：随机攻击是指攻击者对航空通信网络“一无所知”，是一种“零信息攻击模式”，只能采取随机方式攻击整个航空通信网络的作战实体；而蓄意攻击是指攻击者掌握了完整的航空通信网络信息，依据重要度准则，按优先等级依次选择重要的作战实体进行攻击，是一种“完全信息的攻击模式”。然而，处于实际对抗中的航空通信网络，绝大多数情况下面临的既不是“零信息攻击”，也不是“完全信息攻击”，而是“不完全信息”攻击，即攻击者只能够获取通信网络的部分信息。因此，本文从航空通信网络的实际出发，构造了一种不完全信息条件下的攻击策略。

在不完全信息条件下，其攻击策略主要取决于两个要素：一是攻击者所获得的敌方网络的已知区域Ω；二是明确节点的攻击方式，即攻击模式。

2.1 计算已知区域

本文将确定已知区域Ω的过程转化成一个不等概率的抽样问题［15］。不等概率抽样的关键是确定每个节点的入样概率，其与该节点的某一辅助变量（即航空通信网络中节点的某些自身属性）的大小成正比。确定已知区域的计算步骤如下。

2.1.1 参数计算

（1）Ω的广度参数α∈［0，1］，表征在整个航空通信网络中，已知区域内节点数量占所有节点数量的比例，α值越大表示已知区域越大。当α＝0时，E＝Ø，表示攻击者对航空通信网络的信息一无所知，对应随机攻击模式；当α＝1时，表示攻击者获得了整个航空通信网络的全部信息，对应蓄意攻击模式。

（2）Ω的精度参数δ∈［0，∞），反映已知区域总体随机抽样到重点节点的精度。抽样的总体对应航空通信网络中节点的集合V，样本容量为αN对应已知区域Ω的大小。

2.1.2 节点入样概率

本文中航空通信网络的节点越重要，入样概率越大。而节点的重要度与攻击者攻击航空通信网络的目的有关，通常设定节点价值越高越重要，节点层次越高越重要，节点交换信息程度越高越重要。因此，本文不是根据航空通信网络及其相关属性直接计算每个节点的入样概率，而是给出了一个基于节点重要性排序的入样概率计算方法。具体计算方法如下。

首先根据节点重要度由高到低的顺序对节点进行排序，li代表节点vi的次序，li∈｛1，2，…，N｝。然后，构造节点vi的辅助变量ωi＝l。则入样概率可定义为

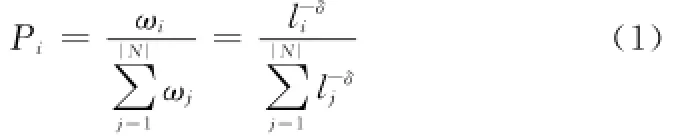
显然，当δ越大，节点重要度排名靠后的节点的辅助变量ωi＝的值越小，该节点的入样概率相比于排名靠前的节点的入样概率所占份额就越小，因此，节点重要度越大的节点入样概率越大。

综上，假设Ωij表示设定的第i种广度和精度参数条件下，通过第j次抽样得到攻击者的已知区域，则生成一个攻击者的已知区域Ωij的过程如下：

步骤1 设定攻击者已知区域的广度和精度参数αi和δi；

步骤2 根据节点的重要度判定准则，对节点进行排序，得到节点的次序li；

步骤3 计算每个节点的入样概率Pi；

步骤4 根据节点的入样概率，从V中抽取m＝［αN］个系统单元。

通过设定f组广度和精度参数，每组参数在仿真实验时进行g次抽样，可以得到f·g组作为攻击者的已知区域

其中，θi＝θi（αi，li）＝｛Ωi1，Ωi2，…，Ωig｝。

2.2 确定攻击模式

本文采用的航空通信网络的蓄意攻击模式为：先攻击已知区域中的节点，对于该区域的节点，按照航空通信网络中节点重要度从大到小依次打击；待已知区域所有节点都遭受攻击后，再攻击未知区域内的节点，对于该区域的节点，采用随机攻击模式。节点遭受攻击时，分别移除该节点，以及与该节点相连接的所有边。

3 级联失效模型及鲁棒性度量方法

3.1 航空通信网络失效模型

当航空通信网络发生级联失效时，其过程包括3个阶段：

（1）稳定工作阶段。航空通信网络的所有作战实体的通信负载都在其工作负载范围内正常运行。

（2）负载传播阶段。当航空通信网络中的某个作战实体遭到外部攻击时，通往该实体的信息必须重新选择通信路径，这种信息分流将给新通信路径上的作战实体的通信能力造成压力。一旦某作战实体的信息总量超出其信息处理能力时，该节点的工作效率会迅速下降，并可能造成节点失效，使得新失效节点的通信负载需要分配到其他节点。

（3）失效终结阶段。在以下两种情况下，航空通信网络的级联失效将结束：一是作战实体相继失效，并造成整体通信网络遭到严重破坏，失去工作能力；二是作战实体失效造成的影响范围有限，航空通信网络达到一种自组织平衡状态。

基于上述分析，针对信息流动的结构特征，定义航空通信网络中，作战实体的通信负载为在单位时间内通过该节点的信息总量，其值设定为节点的介数［16］，并定义作战实体的通信容量与其初始通信负载成正比，即

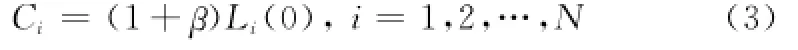
式中，Ci为节点vi的负载容量；β为容忍系数，β≥0；Li（0）为节点vi的初始负载，设定为节点vi在初始网络中的介数。本文用节点负载容量表征节点权值pvi，则pvi＝Ci。

航空通信网络中一个作战实体遭敌攻击并发生失效，会导致经过该节点的通信负载的重分配。假设当前失效重分配次数为T，节点vs为未失效节点，则vs新的负载更新为

式中，ΔLs为节点vs的本轮负载增量，它受自身负载能力和与失效节点间的距离两个因素影响。

定义距离dij表示航空通信网络G中任意两个作战实体vi和vj之间的最短路径上所有边权值之和，这里的边权值主要是指航空通信网络中两个作战实体之间的通信时延。如果vi到vj不可达，则dij→∞。

距离dij表示节点vi和节点vj之间进行正常通信的难易情况，dij值越大，节点间通信时延越长，通信难度越大。

则ΔLs可定义为

式中，ΦT为失效重分配次数T时的失效节点集合；ΓT为失效重分配次数T时的未失效节点集合。

在负载重分配后，需要判断调整负载的节点vs是否失效。若Ls（T＋1）≤Cs，则节点vs此轮不失效；若Ls（T＋1）＞Cs，则节点vs此轮失效，并触发负载重分配。如果所有节点的负载不超过其通信容量，则级联失效结束。

3.2 鲁棒性度量方法

为衡量级联失效对整个网络G的破坏力，本文借鉴文献［17］的方法，用网络效率度量航空通信网络的鲁棒性。

定义网络效率E（G）为所有通信链路通信时延的平均值，用来表示网络中所有节点对之间的平均接近程度［17］，即

式中，N为网络中的节点数目；dij为节点i与节点j之间的距离。

4 仿真结果与分析

对航空通信网络的鲁棒性进行分析，本文构造节点规模为100、边数取值范围为［300，400］的无权无向网络，运用Matlab对本文模型进行仿真（整个网络没有孤立节点）。在设置攻击模式时只考虑航空通信网络中节点的移除。

仿真实验1 广度参数α对航空通信网络鲁棒性的影响

本文首先对在不同攻击信息广度参数α条件下航空通信网络的鲁棒性进行仿真，设定精度参数δ＝1，节点容忍系数β＝0.4，仿真结果如图1所示，图中横坐标为移除节点占所有节点的比例，纵坐标为网络效率。

图1 不同广度参数下网络效率随节点移除比例变化图

从图1中可以看出，随着移除节点数量的增加，航空通信网络的鲁棒性呈现下降趋势，其下降速度随广度参数α的增大而增大。也就是说，在随机攻击下，航空通信网络的鲁棒性下降速度最慢；而在蓄意攻击下，航空通信网络的鲁棒性下降速度最快。

仿真实验2 精度参数δ对航空通信网络鲁棒性的影响

本文对在不同攻击信息精度参数δ条件下航空通信网络的鲁棒性进行仿真，设定广度参数α＝0.5，节点容忍系数β＝0.4，仿真结果如图2所示。

图2 不同精度参数下网络效率随节点移除比例变化图

从图2中可以看出，随着δ值的增加，航空通信网络的鲁棒性在下降。综合图1和图2可知，δ值的改变使得网络效率E（G）下降更快，因此，攻击信息精度δ比攻击信息广度α对网络鲁棒性影响更大。进而可知，隐藏部分重要节点信息将大幅度提高复杂网络的鲁棒性，获取少量重要节点的信息可以大幅度降低复杂网络的鲁棒性。因此，相对于对所有网络节点提供代价较高的同等全覆盖保护，对重要节点提供重点保护的成本和实际效果要更好。

仿真实验3 容忍系数β对航空通信网络鲁棒性的影响

该仿真实验主要考察容忍系数（即节点容量）对节点负载、级联失效和网络鲁棒性的影响。设定攻击信息参数组合（α＝0.5，δ＝1），仿真结果如图3和图4所示，图中横坐标为时间步，纵坐标分别为移除节点占所有节点的比例和网络效率。

图3 不同容忍系数下节点移除比例随时间步变化图

从图3和图4中可以看出，当β值较小时，节点级联失效严重。而随着β的增大，网络整体上应对级联失效的鲁棒性得到增强，其原因是网络节点的容量越高，网络容纳局部失效的潜能越强，从而应对级联失效的能力越强。但当β较大时（如图4中β＝2时），继续增大β值，并不能明显增强网络鲁棒性；而当β值很大时（如图4中β＝10时），网络效率E（G）也会随着节点遭受攻击而逐渐下降，并产生级联失效。因此，追求网络节点的高容量并不一定能使网络避免级联失效。

图4 不同容忍系数下网络效率随时间步变化图

5 结束语

本文对航空通信网络的鲁棒性问题进行了研究，针对航空通信网络会遭敌攻击的实际情况，引入了一种不完全信息条件下的复杂网络攻击模型，给出了不完全信息条件下的攻击模型的具体步骤和参数设置。在航空通信网络中，由于某个节点失效可能会影响到其他正常节点，设计了一种航空通信网络节点级联失效模型，并给出了航空通信网络的鲁棒性度量方法。最后，通过仿真实验，分析了不完全信息条件下的复杂网络攻击模型和级联失效模型中的各个参数对航空通信网络鲁棒性的影响，结果表明，对重要节点提供重点保护的实际效果要明显好于对所有节点同等全覆盖保护，但是一味增强重要节点的负载能力，并不一定能使网络避免级联失效。本文的研究成果为军事系统复杂网络鲁棒性度量和分析提供了一种新的研究思路。

［1］Department of Defense．The Implementation of network-centric warfare［R］．Washington：The Report of DoD Office of Force Transformation，2005．

［2］Yang H W，Zhang Y，Yang X Q，et al．Complex networks and review of research in military field［J］．Journal of Systems Science，2013，21（1）：84- 87．（杨宏伟，张勇，杨学强，等．复杂网络及其在军事领域中的应用研究综述［J］．系统科学学报，2013，21（1）：84- 87．）

［3］Moreau L．Stability of multi-agent systems with time-dependent communication links［J］．IEEE Trans.on Automatic Control，2005，50（2）：169- 181.

［4］Ludema M．Domain knowledge navigating；course ware for a masters in transport＆infrastructure［C］∥Proc.of the World Conference on E-Learing in Corporate，Government，Health-care，and Higher Education，2005：1334- 1341.

［5］Chen Y，Zhao J C，Qi H．Reserarch on robustness of the layered complex networks［J］．Acta Armamentarii，2009，30（6）：839-843．（陈晔，赵金超，齐欢．分层复杂网络的鲁棒性研究［J］．兵工学报，2009，30（6）：839- 843．）

［6］Zhu T，Chang G C，Zhang S P，et al．Research on model of cas cading failure in command and control based on complex networks［J］.Journal of System Simulation，2010，22（8）：1817-1820．（朱涛，常国岑，张水平，等．基于复杂网络的指挥控制级联失效模型研究［J］．系统仿真学报，2010，22（8）：1817- 1820．）

［7］Bao Z J，Cao Y J，Ding L J，et al．Comparison of cascading failures in small-world and scale-free networks subject to vertex and edge attacks［J］．Physica A：Statistical Mechanics and its Applications，2009，388（20）：4491- 4498．

［8］Fang X L，Yang Q，Yan W J．Modeling and analysis of cascading failure in directed complex networks［J］．Safety Science，2014，65：1- 9．

［9］Zhang J H，Xu X M，Hong L，et al．Attack vulnerability of sel

forganizing networks［J］．Safety Science，2012，50：443- 447.［10］Bao Z J，Cao Y J．Cascading failures in local-world evolving

networks［J］．Journal of Zhejiang University Science A，2008，9（10）：1336- 1340.

［11］Xia Y X，Fan J，Hill D．Cascading failure in Watts-Strogatz small-world networks［J］．Physica A：Statistical Mechanics and its Applications，2010，389（6）：1281- 1285.

［12］Wei D Q，Luo X S，Zhang B．Analysis of cascading failure in complex power networks under the load local preferential redistribution rule［J］．Physica A：Statical Mechanics and its Applications，2012，391（8）：2771- 2777．

［13］Dou B L，Wang X G，Zhang S Y．Robustness of network against cascading failures［J］．Physcia A：Statistical Mechanics and its Applications，2010，389（11）：2310- 2317.

［14］Cao X B，Hong C，Du W B．Improving the network robustness against cascading failures by adding links［J］．Chaos，Solitons &Fractals，2013，57：35- 40.

［15］Wu J，Tan Y J，Deng H Z，et al．Model for invulnerability of complex networks with incomplete information based on unequal probability sampling［J］．Systems Engineering-Theory& Practice，2010，30（7）：1207- 1217．（吴俊，谭跃进，邓宏钟，等．基于不等概率抽样的不完全信息条件下复杂网络抗毁性模型［J］．系统工程理论与实践，2010，30（7）：1207- 1217．）

［16］Freeman L C．A set of measures of centrality based upon betweenness［J］．Sociometry，1977，40（1）：35- 41．

［17］Zhou X，Zhang F M，Zhou W P，et al．Evaluating complex network functional robustness by node efficiency［J］．Acta Physica Sinica，2012，61（19）：1- 7．（周漩，张凤鸣，周卫平，等．利用节点效率评估复杂网络功能鲁棒性［J］．物理学报，2012，61（19）：1- 7．）

Method to analyse the robustness of aviation communication network based on complex networks

ZHANG Chao1，ZHANG Feng-ming1，WANG Ying1，WU Hu-sheng2
（1.Equipment Management and Safety Engineering College，Air Force Engineering University，Xi’an 710051，China；2.Materiel Engineering College，Armed Police Force Engineering University，Xi’an 710086，China）

In order to deal with the problem that the actual military aviation communication network suffers the enemy attack，an attack model for complex network with incomplete information is proposed．The cascading failure principle is analyzed，and the method for robustness measure is proposed．At last，the simulation analysis result of the aeronautical communication network’s robustness is provided，which is under different parameter conditions of the incomplete information attck model and the cascading failure model．The result shows that the proposed method is feasible and valid．

complex network；aeronautical communication network；robustness；incomplete information；cascading failure

N 949

10．3969／j．issn．1001-506X．2015．01．29

张超（1986-），男，博士研究生，主要研究方向为信息系统工程与智能决策、复杂系统与复杂网络。

E-mail：armstrong1027＠163．com

张凤鸣（1963-），男，教授，博士研究生导师，博士，主要研究方向为信息系统工程与智能决策、复杂系统与复杂网络。

E-mail：25728042＠qq．com

王瑛（1967-），女，教授，博士研究生导师，博士，主要研究方向为信息系统工程与智能决策、复杂系统与复杂网络。

E-mail：15029007368＠163．com

吴虎胜（1986-），男，博士研究生，主要研究方向为进化计算、智能数据挖掘、信息系统工程与智能决策。

E-mail：wuhusheng0421＠163．com

1001-506X（2015）01-0180-05