基于自适应聚类流形学习的增量样本降维与识别

2015-06-19杨静林唐林波赵保军

系统工程与电子技术 2015年1期

关键词：高维降维增量

杨静林，唐林波，宋丹，赵保军

（1．北京理工大学信息与电子学院，北京100081；2．北京电子工程总体研究所，北京100854）

基于自适应聚类流形学习的增量样本降维与识别

杨静林1，唐林波1，宋丹2，赵保军1

（1．北京理工大学信息与电子学院，北京100081；2．北京电子工程总体研究所，北京100854）

为了解决局部线性嵌入（locally linear embedding，LLE）流形学习算法无法自适应确定重构区间和不能进行增量学习等问题，提出了一种自适应聚类增量LLE（clustering adaptively incremental LLE，C-LLE）目标识别算法。该算法通过建立高维非线性样本集的局部线性结构聚类模型，对聚类后的类内样本采用线性重构，解决了LLE算法样本重构邻域无法自适应确定的问题；通过构建降维矩阵，解决了LLE算法无法单独对增量进行降维和无法利用增量对目标进行识别的问题。实验表明，本文算法能够准确提取高维样本集的低维流形结构，具有较小的增量降维误差和良好的目标识别性能。

流形学习；局部线性嵌入；增量降维；目标识别；分裂聚类

0 引言

在目标识别与分类过程中，通常需要对具有标签信息的训练样本进行学习，并根据一定准则建立相关的决策模型，以对未知标签信息的测试样本进行分类［1］。训练样本和测试样本往往具有较高的维度，数据冗余性大，处理时容易陷入“维数灾难”［2］，因此获取高维样本的低维结构已成为快速准确地识别目标的重要保障［3］。

流形学习方法是近年兴起的一种非线性降维方法，与线性降维不同，其思想是寻找样本集的内在规律［4-5］，将高维空间中的数据映射到一个低维空间（即低维流形）中，达到降维的目的［6］。2000年，Saul和Roweis提出局部线性嵌入（locally linear embedding，LLE）流形学习算法［7］，LLE算法具备几何意义直观和具有整体解析最优解等优点［8］，但该算法不具备增量学习的能力，只能对样本集批量处理。而当前的目标识别系统中，测试样本往往以增量的形式出现，如果每一个新增测试样本均与训练样本集一起进行批量降维和识别，无疑会耗费大量时间［9］。

目前，针对LLE算法所提出的增量学习算法较少。Saul在原算法的基础上提出了线性化增量LLE算法［10］。首先计算新增样本与训练样本集中所有样本的距离，并通过前k个最小距离样本构建权值向量矩阵，找到这k个高维样本所对应的低维投影，对新增样本的低维表示进行重构。该方法假设训练样本的权值矩阵不会因新样本的加入而发生改变，但实际上新样本的加入会导致局部权值矩阵发生变化，降维误差较大。Kouropteva等［11］在假定原有特征值不变的基础上提出了LLE的增量算法，但该方法将原本问题转化为特征值求解问题又转化为最优化问题，而且特征值没有更新［12］。

针对上述问题，本文提出了基于自适应聚类增量LLE（clustering adaptively incremental LLE，C-LLE）算法。该算法分析非线性样本集的局部线性度量，采用分裂聚类方法，自适应地提取样本集中的线性结构，解决了LLE算法样本重构邻域无法自适应确定的问题；通过构建显示降维矩阵，直接对增量样本进行低维投影，解决了LLE算法无法单独对增量进行降维和无法利用增量对目标进行识别的问题。

1 LLE算法流程及本文思路

1.1 LLE算法简介

令高维样本集X＝［x1，x2，…，xN］，X中每一个样本为xi＝［xi1，xi2，…，xiD］T。X的低维流形表示为Y＝［y1，y2，…，yN］，其中yi＝［yi1，yi2，…，yid］T，d＜D。

LLE算法降维流程如下所示：

步骤1 计算各样本之间的欧式距离

步骤2 获取每个样本的k个最邻近样本，计算样本的局部重建权值，定义损失函数

式中，xi＋j（j＝1，2，…，k）表示xi的k个最近邻样本；wij是xi与xi＋j的重构权值，定义权值矩阵W＝［w1，w2，…，wN］，W中的每一个元素wi＝［wi1，wi2，…，wik］T，且满足条件eTwi＝1，ek×1＝［1，1，…，1］T。

步骤3 计算权值矩阵W。首先需要构造局部协方差矩阵

Q中的每一个元素qij表示为

与eTwi＝1相结合，求取wi

步骤4 将所有样本映射到低维流形空间将矩阵M的特征值从小到大排列，剔除第一个近似于0的特征值，其余2～d＋1个特征值所对应的特征向量即为Y。

1.2 LLE不具备增量学习的原因及本文思路

流形学习算法假设非线性流形由局部线性的流形结构拼接而成。LLE算法根据这种局部线性的思想利用样本xi的k邻域对xi进行重构，LLE降维效果与k值相关。

图1（a）为LLE算法的高维样本邻域结构。LLE算法对不同样本的线性重构邻域均采用固定的邻域数目k。当k较大时，邻域包含了非线性结构；当k较小时，会造成重构邻域无法包含所有呈线性关系的样本。为了解决这个问题，LLE采用了重叠的局部线性邻域结构，因此在邻域相互重叠的情况下对非线性样本集整体进行处理，无法提取显式的降维矩阵，不能进行增量降维。

图1（b）为本文算法的邻域结构。本文算法认为LLE算法虽然将样本集X表示为一个重叠的线性重构的整体，但实际上可按照线性程度将X划分为多个独立的线性子类，类内样本呈线性关系，各类之间呈非线性关系。类内样本由类内其余样本线性重构，不可由其他类样本重构，这也解决了邻域数目k不可变的问题。由于类内样本是线性的，因此可以对每一个线性类提取单独的显式降维矩阵，进而达到增量降维的目的。

图1 LLE与本文算法邻域结构

2 高维样本集局部线性结构聚类

2.1 非线性样本集的局部线性结构表达

根据流形假设，设计了如下非线性样本集的局部线性表达方法。

图2（a）为二维的非线性流形，图2（b）为划分的二维流形局部线性结构。为得到紧凑的局部线性结构，需要根据样本集的线性程度对样本进行聚类。

图2 二维非线性数据及其局部线性结构

文献［13- 14］提出通过局部主成分分析（principal component analysis，PCA）可以度量流形的线性程度。PCA算法通过对样本集X的协方差矩阵进行奇异值分解（singular value decomposition，SVD）来获得特征值［λ1，λ2，…，λD］和特征向量矩阵SD×D，将前d个最大特征值所对应的特征向量S′D×d作为样本集X的投影矩阵，构建如下目标函数：

当X为理想线性数据时，S′TS′＝I；若样本集非严格线性，存在误差ε＝‖S′TS′－I‖2。该目标函数的意义为：样本xi进行低维投影后再对其进行高维重构，并计算重构结果与原样本的误差，对样本集X的误差进行累计，误差越小说明X的线性程度越好。

用550个伊利诺伊大学（University of Illinois at Urbana-Champaign，UIUC）汽车图像组成的正类样本和500个负类样本组成训练样本集X。对于不同维数d，误差ε（X）如表1所示。结果表明，高维样本X所降至的维度d越小，高维重构后误差ε（X）越大（将1 584维样本降至1 500维时，重构误差仅为1.32×10－12）。因此，对于不同样本集，在维数d一定的情况下，线性化程度越高的样本集PCA降维后误差ε（X）越小。

表1 不同维度下非线性结构数据的PCA降维误差

2.2 样本集线性结构的分裂聚类方法

在提出样本集高维非线性数据集的局部线性结构表达方法后，首要的任务就是如何将非线性的数据集按照其线性结构进行聚类。为解决这一问题，本文提出了线性结构分裂聚类的方法。

分裂聚类算法是在K均值聚类算法的基础上提出的［15］。该方法无需设定初始聚类数目，能自适应对样本集聚类。

图3为样本集线性结构的分裂聚类方法示意图。线性结构的分裂聚类可以看作是一个聚类窗口在样本集上不断分裂收缩的过程，随着聚类半径的缩小，类内样本的线性程度逐渐提高。若分裂所获得的聚类结构中线性程度仍然不满足要求，则继续对不满足线性度要求的类进行分裂，直至类内样本集满足线性度要求。

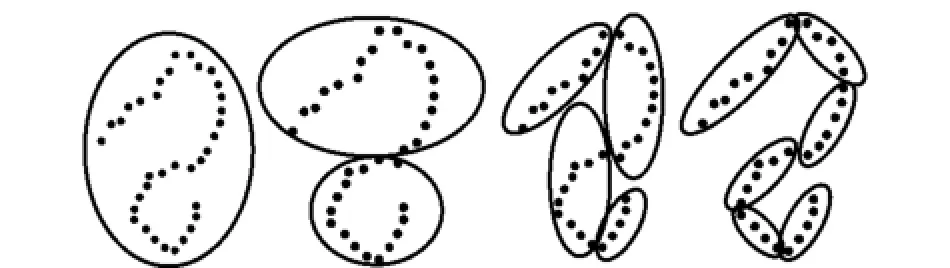
图3 样本集线性结构的分裂聚类方法

在描述分裂聚类算法步骤前，首先定义样本距离和类内均值：用d（xi，xj）表示样本欧式距离，Uz表示第z个类别的类内均值。对于样本集X，分裂聚类步骤如下：

步骤1 初始化聚类中心

设定X的初始类别数z＝1，随机抽取1个样本｛xi，i∈［1，N］｝作为初始聚类中心，即xc1＝xi。

步骤2 类分裂

步骤2.1 计算所有样本到聚类中心｛xcz，z∈［1，2，…，K］｝的欧式距离d（xcz，xi），寻找距离xcz最远的样本xmz；

步骤2.2 分裂聚类中心xc（z＋1）＝xmz，聚类数目变为K＋1，计算所有样本到聚类中心xcz的距离，将样本归到其最近的类Cz中；

步骤2.3 调整聚类中心，将中心移动到均值处，即xcz＝Uz。

步骤3 线性度判别

计算每一个类内的线性度误差ε（xz）′，在l个不同维度下，对于给定阈值η，若线性度满足要求，分

t＝1裂终止，否则重复步骤2～步骤3。

综上所述，分裂聚类能够满足每一类子集中的线性样本尽可能多，并且类间不交叠。

图4为阈值η与聚类数量c的变化关系。可以看出，随着η的下降，样本集聚类的数量不断增加，类内样本线性程度不断提高。当η减小到一定程度时，聚类数量近似收敛。

图4 不同阈值下的聚类数量

3 C-LLE增量学习算法

3.1 高维样本集的C-LLE低维流形学习

通过对高维样本集的局部线性结构聚类，得到一组线性结构样本集。用V表示流形线性结构聚类个数，Nm表示第m类中的高维样本个数，高维样本总数N＝N1＋N2＋…＋NV。由于每一类中的样本均为线性结构，根据LLE算法定义，同类中的每一个样本均可由其余Nm－1个样本进行线性重构。样本结构矩阵权值表示为Wi＝［wi1，wi2，…，wiD］T，式（2）变形如下：

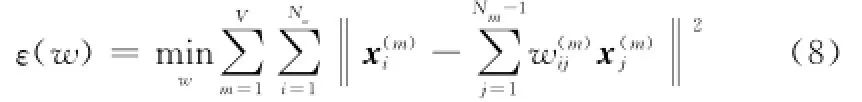
由于不同类样本数目Nm不同，为方便计算，引入矩阵H，将式（8）变为

h（m）j满足如下条件：

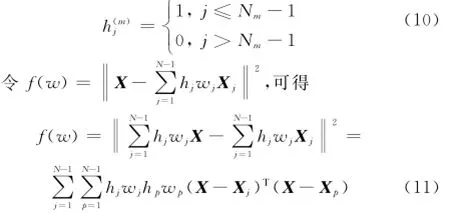
令Qjp＝（X－Xj）T（X－Xp），可得

综上，可得矩阵形式为

令W′＝HW，可得

将eTW1＝1（e＝［1，1，…，1］）作为约束条件，令g（W′）＝eTW1－1，用拉格朗日描述子对f（W′）进行极小化

令e1×D＝［1，1，…，1］，可得

将式（15）结合约束eTW′＝1，解方程得

将所有样本映射到低维空间

由于低维流形与高维样本具有相同的结构，因此对每一个D维样本右乘投影矩阵Z，进行线性变换，可得d维流形。

其中，对高维样本矩阵进行变换

投影矩阵可以表示为

将高维样本集X用低维流形Y表示

计算矩阵M′的特征值，将特征值从小到大排列。剔除第一个接近0的特征值，取第2～d＋1个特征值所对应的特征向量组成投影矩阵Z。这样，每一个线性类CV都得到一个降维投影矩阵ZV。

3.2 C-LLE增量样本降维与识别

当对增量样本（即测试样本）xN＋1进行识别时，识别算法步骤如下：

步骤1 用Ci的投影矩阵Zi对增量样本xN＋1和Ci中的样本进行降维

步骤2 从yi1，yi2，…，yiNV中找到yi（N＋1）中的K个邻域NHk（yi（N＋1））；

步骤3 用N Hk（yi（N＋1））重构yi（N＋1），并由重构误差来度量yi（N＋1）与Ci的距离

其中，Pik为距离权值，可通过核密度加权的方法计算

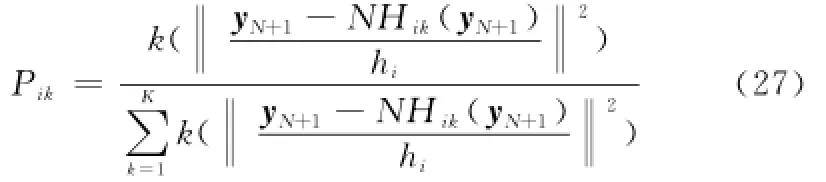
ri为核密度半径，计算公式如下：

最后对训练样本进行有监督分类，从而确定yi（N＋1）的类别，完成目标识别。

4 实验结果与分析

为测试本算法的性能，本文分别将Saul和Kouropteva的LLE增量算法与本文算法进行对比。验证共分两部分：第一部分是对样本集的降维，第二部分是对增量样本的降维和识别。实验所选数据库为UIUC汽车目标识别数据库。仿真软件为Matlab 2010a，计算机主频为双核2．5 GHz，内存2 GB。

4.1 样本集降维效果对比与分析

Saul和Kouropteva的算法中关于数据集的降维部分均应用LLE算法，因此本部分对比LLE算法与本文C-LLE算法的降维效果。

为增强数据可视化效果，通过LLE算法和本文算法分别将数据集的高维特征向量降至2维，两种降维方法如图5所示。

图5 UIUC数据库低维流形结构

图5 为汽车识别数据库通过LLE算法和本文算法降至2维流形的效果对比。图中的“＋”为负类样本的低维流形，“．”为正类样本的低维流形。在LLE中，k≤12时其流形结构会被破坏，k≥16会带来噪声，在k＝13时，LLE降维取得较好的结果，但可以看出姿态和外观差距较大的汽车样本与负类样本混叠较为严重。在二维情况下，本文算法可以将正负两类样本进行较好的分离，仅有少量样本发生混叠。

通过实验可以得出本文算法的降维效果优于LLE算法。

4.2 增量目标识别效果对比与分析

本小节从降维误差、目标识别效果和运算时间3个方面，分别对Saul的线性LLE增量算法、Kouropteva的LLE增量算法与本文增量算法进行比较。

4．2．1 增量降维误差对比

从UIUC测试集中选取85幅图像作为增量样本，增量样本的低维流形误差如下：

式中，y＾i为新增样本xi按照3种增量LLE降维方式计算的结果；yi为新增样本归并到训练样本集后经LLE或本文算法降维后得到的结果；error∈［0，1］。

图6为不同维度下3种增量降维算法的增量降维误差。

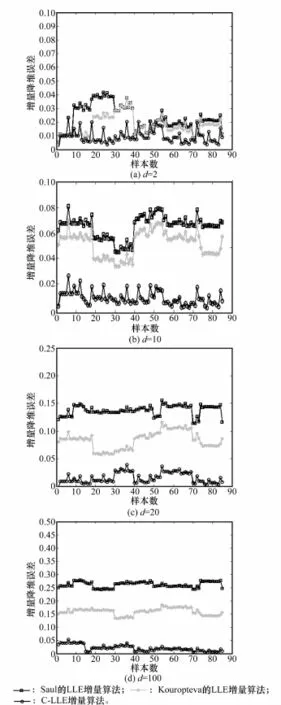
图6 不同维度下3种算法增量降维误差

从图6可以看出，随着低维流形维度的增加，增量降维误差不断增加。由于不同样本集均存在其固有的本征维数，因此低维流形维度d并不是越低越好。Saul的增量LLE算法中，由于代价矩阵M和增量低维流形Ynew的重构邻域没有更新，因此随着维度增加，低维流形重构误差增加明显，当低维流形维度d＝50时，低维流形的重构最大误差为30.5%，平均误差为27．4%；Kouropteva的LLE增量算法对代价矩阵M进行了更新，增量降维误差来自于增量样本的低维流形的重构邻域，可以看出在d＝50时，85个增量样本最大误差为19.6%，平均误差为15．7%；C-LLE的增量算法是局部线性降维，不需要对增量低维流形Ynew的重构邻域进行更新，增量降维误差仅来自于某一类Ci线性度较高的样本的代价矩阵M，在d＝50时，85个增量样本最大误差为6%，平均误差为0．9%。

4.2.2 目标识别效果对比

为测试算法的目标识别效果，选择了200组汽车目标图像进行识别，部分汽车目标图像的3种增量识别算法效果对比如图7所示。图7为对1 584维特征向量降至20维时目标识别效果。通过图7可以看出，在d＝20情况下，由于增量降维误差的缘故，C-LLE增量目标识别效果好于Saul和Kouropteva的LLE增量算法。

图7 3种增量LLE算法识别效果对比

漏检率与误检率是度量目标识别效果的指标，漏检率与误检率构成DET曲线。本文采用200幅正类（汽车）图像与200幅负类（场景）图像作为测试样本，在不同维度下生成的DET曲线如图8所示。

图8 3种增量LLE算法DET曲线对比

通过图8可以看出，在d＝2时，3种算法均具有较高的漏检率和误检率。随着流形维度d的增加，漏检率和误检率逐渐降低，在d＝20时，3种算法的DET曲线中漏检率和误检率均达到最低，即d＝20为低维流形的本征维数。当d＞20时，随着增量降维误差的增大，Saul和Kouropteva的LLE增量算法目标识别效果变差，漏检率和误检率逐步上升。而C-LLE算法的增量降维误差随着维数增加变化平缓，漏检率和误检率趋于稳定，识别效果较好。本征维数的确定也是流形学习的一个难点，很难直接确定高维样本低维流形的本征维数，当维数增大到一定量值后，C-LLE算法增量降维和识别效果比较稳定，因此C-LLE算法的增量降维和目标识别效果优于前两者。

4.2.3 算法处理时间对比

当对Xnew进行处理时，Saul的LLE增量算法耗时部分主要为新增样本k邻域的确定、权重向量Wnew的计算；Kouropteva的LLE增量算法耗时部分主要为最优化minε（Y）＝YMYT－diag（λ1，λ2，…，λd）；C-LLE增量算法不需要对所有样本进行搜索确定邻域，主要耗时部分为增量样本的低维投影。

算法处理时间测试条件如下：

（1）样本集选择UIUC汽车目标识别数据库（训练样本1 100个，维度1 584）。

（2）LLE邻域数量k＝14。

（3）低维流形维度d＝10。

3种算法的处理时间对比如图9所示。通过对比可以看出，C-LLE增量算法的运行时间为0．65 s，远低于Saul和Kouropteva增量LLE算法（4．47 s和7．13 s）的运行时间。

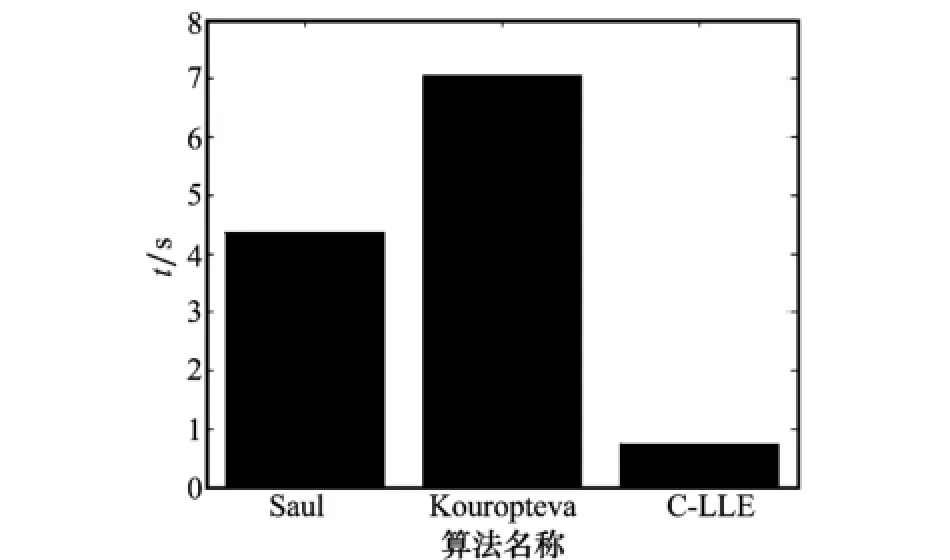
图9 3种算法运算速度对比

5 结论

针对LLE流形学习算法无法自适应进行线性重构以及不具备增量学习能力的问题，提出了一种C-LLE目标识别算法。该方法分为高维非线性数据局部线性聚类、样本集低维流形学习和增量样本识别3个部分，解决了高维样本的重构邻域无法自适应确定以及无法对增量样本进行增量降维和识别的问题。实验从高维样本集降维效果、增量样本识别效果和算法速度等3方面对比了Saul和Kouropteva的增量LLE算法与本文算法的性能，结果表明本文算法的性能优于前两者。

［1］Cui J，Li Z，Gao J，et al．The application of support vector machine in pattern recogntion［C］∥Proc.of the International Conference on Control and Automation，2007：3135- 3138．

［2］Faruqe M O，Hasan M A M．Face recognition using PCA and SVM［C］∥Proc.of the 3rd International Conference on Anti-Counterfeiting，Security，and Identification in Communication，2009：97- 101．

［3］Wen C，Zhu Q．Dimension reduction analysis in image-based species classification［C］∥Proc.of the International Conference on Intelligent Computing and Intelligent Systems，2010：731- 734．

［4］Yu P F，Yu P C，Xu D．Comparison of PCA，LDA and GDA for palmprint verification［C］∥Proc.of the International Conference on Information Networking and Automation，2010：148- 152．

［5］Sang M L，Abbott A L，Araman P A．Dimensionality reduction and clustering on statistical manifolds［C］∥Proc.of the International Con-ference on Computer Vision and Pattern Recognition，2007：1- 7．

［6］Zhang Z Y，Wang J，Zha H Y．Adaptive manifold learning［J］．IEEE Trans.on Pattern Analysis and Machine Intelligence，2012，34（2）：253- 265．

［7］Roweis S T，Saul L K．Nonlinear dimensionality reduction by locally linear embedding［J］．Science，2000，290（5500）：2323- 2326．

［8］Zhao S L，Zhu S A．Face recognition by LLE dimensionality re

duction［C］∥Proc.of the International Conference on Intelligent Computation Technology and Automation，2011：121- 123．

［9］Zhu M H，Luo D Y．Incremental locally linear embedding algorithm based on inverse iteration method［J］．Computer Engineering and Applications，2010，46（17）：176- 178．（朱明旱，罗大庸．基于逆迭代的增量LLE算法［J］．计算机工程与应用，2010，46（17）：176- 178．）

［10］Saul L K，Roweis S T．Think globally，fit locally：unsupervised learning of nonlinear manifolds［J］．The Journal of Machine Learning Research，2003，4（1）：119- 155．

［11］Kouropteva O，Okun O，Pieti Kainen M．Incremental locally linear embedding algorithm［J］．Pattern Recognition，2005，38（10）：1764- 1767．

［12］Li H S，Cheng L Z．Research on incremental Hessian LLE algorithm［J］．Computer Engineering，2011，37（6）：159- 161．（李厚森，成礼智．增量Hessian LLE算法研究［J］．计算机工程，2011，37（6）：159- 161．）

［13］Wang L，Wu C D，Chen D Y，et al．Exploring linear homeomorphic clusters on nonlinear manifold［J］．Acta Automatica Sinica，2012，38（8）：1308- 1320．（王力，吴成东，陈东岳，等．非线性流形上的线性结构聚类挖掘［J］．自动化学报，2012，38（8）：1308- 1320．）

［14］Zhang Z Y，Zha H Y．Principal manifolds and nonlinear dimensionality reduction via tangent space alignment［J］．Society for Industrial and Applied Mathematics Journal on Scientific Computing，2005，26（1）：313- 338．

［15］Sun J G，Liu J，Zhao L Y．Clustering algorithms research［J］．Journal of Software，2008，19（1）：48- 61．（孙吉贵，刘杰，赵连宇．聚类算法研究［J］．软件学报，2008，19（1）：48- 61．）

Incremental sample dimensionality reduction and recognition based on clustering adaptively manifold learning

YANG Jing-lin1，TANG Lin-bo1，SONG Dan2，ZHAO Bao-jun1
（1.School of Information and Electronics，Beijing Institute of Technology，Beijing 100081，China；2.Beijing Institute of Electronic System Engineering，Beijing 100854，China）

To solve the problem that incremental learning of locally linear embedding（LLE）cannot get reconfiguration neighborhood adaptively and powerlessly，a target recognition method of clustering adaptively incremental LLE（C-LLE）is proposed．Firstly，the clustering model of the clustering locally linear structure of high-dimensional data is build，so it is able to solve the problem of neighborhood adaptive reconfiguration．Then the proposed algorithm extracts an explicit dimensionality reduction matrix，and the problem of powerlessly incremental object recognition is solved．Experimental results show that the proposed algorithm is able to extract the low-dimensional manifold structure of high-dimensional data accurately．It also has low incremental dimension reduction error and great target recognition performance．

manifold learning；locally linear embedding（LLE）；incremental dimension reduction；object recognition；mitotic clustering

TP 391

10．3969／j．issn．1001-506X．2015．01．32

杨静林（1985-），男，博士研究生，主要研究方向为图像处理、目标检测与识别。

E-mail：yangjinglin＠bit．edu．cn

唐林波（1978-），男，讲师，博士，主要研究方向为目标检测与跟踪、实时图像处理技术。

E-mail：tanglinbo＠bit．edu．cn

宋丹（1984-），男，工程师，博士，主要研究方向为一体化信息处理技术、目标识别与跟踪技术。

E-mail：adanflytosky＠gmail．com

赵保军（1960-），男，教授，博士，主要研究方向为多光谱图像融合、识别与跟踪技术，高分辨图像实时压缩、恢复与传输技术，智能图像处理技术。

E-mail：zbj＠bit．edu．cn

1001-506X（2015）01-0199-07