动态系统故障的混杂传播特征及建模方法

2015-06-27郭健彬杜绍华曾声奎

系统工程与电子技术 2015年1期

关键词：系统故障动态建模

郭健彬，杜绍华，王鑫，曾声奎

（1．北京航空航天大学可靠性与系统工程学院，北京100191；2．可靠性与环境工程技术重点实验室，北京100191；3．北京环境特性研究所，北京100854）

动态系统故障的混杂传播特征及建模方法

郭健彬1，2，杜绍华1，王鑫3，曾声奎1，2

（1．北京航空航天大学可靠性与系统工程学院，北京100191；2．可靠性与环境工程技术重点实验室，北京100191；3．北京环境特性研究所，北京100854）

动态系统的故障传播过程是由离散事件、连续特性及其相互作用共同驱动的，具有显著的混杂特征，为故障规律认知与建模带来了较大的难度。现有研究将故障视为离散随机事件，分析由单元随机故障发生到系统失效的离散故障过程，却忽略了连续特性对故障传播的影响，本质上是对故障混杂传播的工程简化处理，不能真实地描述动态系统的故障规律。首先在分析动态系统故障规律的基础上，给出了离散与连续双维度下的动态系统故障混杂传播的定义，分析了其混杂影响要素以及混杂传播特征；其次，为了完整准确描述混杂特征，借鉴混杂理论在描述离散事件与连续参数相互作用方面的优势，提出了基于随机混杂自动机（stochastic hybrid automata，SHA）的故障混杂传播建模方法；最后通过对某温度控制系统的故障混杂传播过程进行建模和仿真，验证了动态系统故障传播过程中的混杂特征，以及建模方法的可行性。

故障传播；混杂；可靠性；动态系统；随机混杂自动机

0 引言

动态系统故障传播过程是由离散事件（如故障、重构等）、连续特性变化（如应力改变、物理参数退化、性能波动等）以及两者之间的相互作用共同决定的。例如，单元的离散故障会导致系统构型变化或余度减少，进一步引起应力的重新分布或者关键性能指标的突变；而系统应力（如机械应力、热应力、电应力、流体力等）的动态变化以及物理参数（如磨损、裂纹等）的持续退化又对故障产生加速或减速作用，当连续特性超过阈值时会直接导致故障的发生。

现有研究将单元故障作为随机离散事件，重点关注从单元故障发生到系统失效的故障离散传播过程。文献［1］以核电厂供电系统为例，利用动态故障树研究了考虑维修备件情况下系统的离散故障传播过程，文献［2］提出的动态贝叶斯网络能够较好地描述离散故障动态相关性；文献［3］提出了基于Petri网的故障传播模型，仿真了故障传播及其诊断的过程；文献［4］提出基于连续时间Markov链的连锁故障相关性建模方法。

对于一般动态系统，经常出现性能降级等软故障，这些故障对环境载荷、性能波动、参数退化、制造偏差等连续特性比较敏感。上述研究侧重描述故障的离散传播过程，解决系统规模大、相关性复杂等问题，大部分研究将故障完全视为随机事件，却忽略了故障对连续特性的作用，以及连续特性对故障的反作用。随着研究的不断深入，电网领域的部分学者开始研究连续特性变化（电力负载）对故障传播的影响，如文献［5- 6］提出了基于分支过程的负载相关连锁故障建模方法。

结合故障传播技术的发展趋势，论文提出在动态系统故障传播研究中，应该从离散单一维度下的传播逐渐扩展到离散和连续双维度下的传播，即故障的混杂传播，充分考虑离散故障和连续特性之间的相互作用。这样不仅能更真实地描述动态系统的故障传播规律，还能分析得到对各种故障敏感的连续特性，为开展故障原因分析、可靠性优化以及故障诊断提供支持。

论文第1节给出了动态系统故障混杂传播的定义，并分析了混杂传播过程的影响要素与特征；第2节探讨了基于随机混杂自动机的故障混杂传播建模方法，利用模型离散层、连续层、交互层以及层次之间的动态相关性来描述故障的混杂传播过程；第3节通过对某温度控制系统的故障混杂传播过程进行建模和仿真，验证了动态系统故障传播过程中的混杂特征，以及建模方法的可行性。

1 混杂传播定义与混杂特征分析

1.1 混杂传播定义

动态系统故障传播过程中，单元故障、物理参数退化和广义应力变化（如机械应力、电应力、热应力、液体力等）之间表现为两两相互作用，并且受到控制行为的有利调整以及环境因素的不利影响，使故障传播变得更为复杂，表现出混杂性和不确定性。典型故障混杂传播过程如图1所示。

单元故障的发生（状态2）使广义应力x1发生突变，随着应力在系统内的非线性传播，可能导致广义应力xn突破广义强度，造成相关单元的过应力故障或者性能降级故障（状态3）。另一方面，广义应力x1的突变可能导致与其相关的物理参数p1的退化加剧，使p1超过阈值的时间变短，即p1相关的耗损性故障提前发生（状态4）。在应力、参数和故障三者的耦合影响下，驱动故障过程不断发展直至系统故障（状态5）。

将这种由离散和连续因素及其相互作用驱动的动态系统故障传播，称为动态系统故障的混杂传播。传统离散传播将故障视为随机离散时间，只能给出从状态2到状态4（或状态3）的转移概率；而本文综合考虑连续传播和混杂传播后，即可给出状态2到状态4（或状态3）的故障演化过程、故障相关应力、敏感参数以及状态4发生的确切时间等，为后续可靠性设计分析及故障诊断工作提供丰富的参考数据。

图1 动态系统故障混杂传播示例

1.2 混杂要素及特征分析

论文总结了影响动态系统故障传播的5类主要离散和连续因素，即混杂要素：

（1）组成单元的故障事件（离散）；

（2）广义应力的变化（短期连续波动、长期连续降级）；

（3）物理参数由于磨损、腐蚀、老化等机理导致持续退化（连续）；

（4）环境影响（离散突发影响、连续渐变影响）；

（5）自动及人工控制行为（离散重构／维修、连续伺服调整）。

基于上述混杂因素及其耦合作用，可以描述动态系统故障传播的混杂特征。这些特征在动态系统中普遍存在，但在传统离散传播中很难描述。典型特征如下：

（1）单元故障导致物理参数退化过程的加速，如余度系统某单元故障会导致其他单元分担更多的应力，进一步导致工作单元参数的加速磨损或者老化；另一方面物理参数的退化超过容差极限后，又会反过来导致单元故障，进一步导致系统故障。

（2）单元故障会导致某个广义应力的降级或者突变，系统性能降级超过阈值后，会反过来导致系统故障。

（3）物理参数的退化会导致广义应力的退化，而广义应力的变化又对物理参数退化起到加速或减速过程。

（4）环境变化直接导致广义应力的波动，并且会对物理参数的退化速率和单元故障率产生影响。

（5）控制手段会使系统向着远离故障的状态演变，伺服控制可以容忍小扰动，容错控制可以容忍故障发生。

2 故障混杂传播建模方法

混杂理论［7］是近年来在控制领域兴起的一门新技术，已被广泛应用于交通系统、机器人系统、电力系统等领域［8-9］，通过混杂模型可以将“切换”等离散控制信号与连续动态信号统一到同一建模框架下，实现仿真过程中离散模型和连续模型的动态交互。

但现有混杂模型注重描述系统正常工作时的确定性演化过程，对故障状态及随机特征描述不足。如文献［10］中虽给出了随机混杂自动机（stochastic hybrid automata，SHA）的定义，但该模型只考虑了离散状态的切换随机性，在离散状态内部的演化由确定性微分方程驱动。事实上，在离散状态内部，系统的连续演化规律也是受随机性影响的，如环境扰动、输入噪声以及制造误差。

为了能将控制领域的SHA运用到故障混杂传播建模中，论文提出了一种新的SHA模型，更全面地考虑了各种随机因素及其对故障传播的影响。

定义SHA为一个9元组：

式中，Q为离散状态集Q＝｛q1，q2，…，qm｝；X为连续状态空间X＝［x1，x2，…，xn］；E为有限的事件集，包括确定性事件和随机性事件；W＝（u，w）为外部输入集合，u为控制信号，w为扰动信号；Act是指定在每个离散状态q∈Q下的映射，反映系统在该离散状态下的运动规律（如应力变化规律、参数退化规律等），可由随机微分方程和数值仿真模型表示。由于各离散状态表征的故障或工作模式不同，因此各微分方程或仿真模型的结构或参数也不同。Λ为迁移强度函数，Λ→λij（x，t）表示在t时刻，x点处发生从状态qi到qj迁移的瞬时强度；C为迁移关系集合C＝（qi，eij，Γij（x，t），qj），qi，qj分别为起始状态和目标状态，eij为对应的事件，Γij（x，t）为跳变条件。对于确定性跳变

式中，G（x）表示边界判据，对应广义应力x或者物理参数A的阈值。对于随机性跳变

2.1 随机混杂自动机定义

混杂故障传播虽然能更真实地描述系统故障过程，但同时会为建模带来难度，需要将离散的故障状态转移模型与连续的应力模型和参数退化模型有机整合起来，不仅需要实现各类模型之间的动态作用，还要考虑各类混杂要素随机性的影响，这给混杂传播建模带来了很大的难度。论文基于混杂理论初步探讨了动态系统故障混杂传播的建模方法。其中，函数g表示执行状态切换所需满足的瞬时迁移强度λij（x（t））的积累限度。P＝［］为概率分布矩阵，p表示从状态qi到ql的概率；Inv＝（q0，x0，P0）对应初始条件。

2.2 基于SHA的故障混杂传播模型

基于上述SHA模型，系统故障混杂传播模型可表述为离散层、连续层和交互层，结构如图2所示。

图2 系统故障混杂传播模型结构

离散层由自动机模型描述，主要表征长周期尺度下系统正常、降级、维修、故障运行状态q之间的逻辑关系，与传统离散传播模型类似。连续层由随机微分方程描述，主要表征系统在各个离散状态下系统的连续演化规律，包括广义应力模型、退化模型以及故障率模型。广义应力模型描述在离散状态qi下，应力x在物理参数A和B、控制输入u以及环境扰动（Wiener过程d w（t））共同驱动下的动态规律；退化模型描述物理参数A和B在应力x和扰动d w（t）下的变化过程；故障率模型给出由离散状态qi跳变到qj的概率λij，考虑了应力x对故障率的影响。3类模型相互作用，驱动当前离散状态qi下的系统演化。

交互层借助SHA的跳变机制实现离散模型与连续模型间的动态交互。一方面根据离散层的不同故障状态qi执行连续层的模型重构；另一方面实时检测连续层的应力、物理参数及故障率，动态决定离散层跳变到故障状态qj的准确时间，并能判断出故障原因是广义应力（如屈服应力超过强度、性能降级）还是物理参数（如磨损或裂纹超过阈值），或者是偶然故障。

3 案例验证

某温度控制系统包括两个互为冗余的控制回路（PI控制和开关控制）和一个烤箱箱体。PI控制模式是烤箱系统的主要运行模式，保证烤箱温度快速稳定到指定温度Tref＝190°C。当PI控制器故障时，切换为开关控制模式，通过在加热和自然降温之间实现切换，使温度维持在［170℃，210℃］之间，并启动PI控制器的维修过程。

案例做出以下假设：

（1）仅考虑烤箱、PI控制器和开关控制器的故障。当温度超过270℃时，烤箱故障；将PI控制器、开关控制器视为随机事件，故障率随温度变化。λ（x，t）＝h（x）λ0（t），温度系数［11］为

（2）考虑烤箱物理参数的退化。加热系数τ服从均值退化的正态分布τ～N（0.5×e－0.0001t，0.1）。

（3）考虑控制信号噪声影响。设信号噪声为白噪声，信噪比为65 dB。

（4）考虑控制器维修过程修复如旧，衰减系数α＝0.9，累计衰减超过0.5时更换控制器，烤箱不可修。

（5）考虑伺服控制对温度的调节作用。

（6）考虑故障检测，当温度超出［140℃，240℃］，传感器报故。

建模过程如下：

步骤1 根据系统的运行原理，定义系统的主要离散状态，如表1所示。

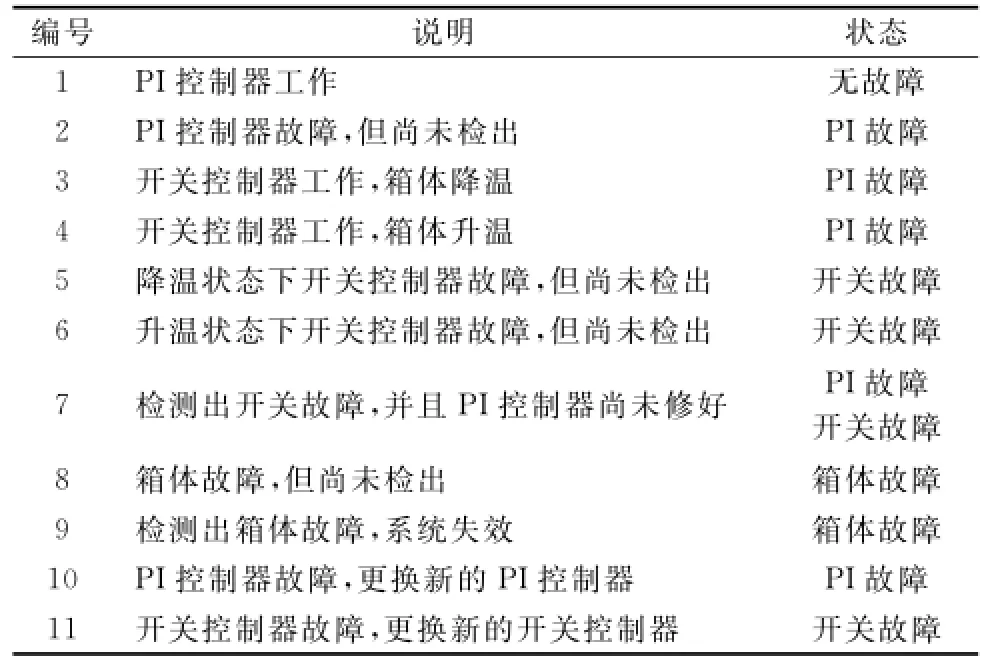
表1 系统离散状态

步骤2 根据系统工作原理、故障状态、退化特征以及噪声分布等，得到系统各个离散状态下的连续状态方程。

步骤3 确定各个离散状态之间的跳变条件，包括随机跳变和确定跳变，建立起连续状态与离散状态间的交互关系。

步骤4 根据上述分析结果，利用Simulink／Stateflow建立温控系统的故障传播模型。在Stateflow中建立离散层和交互层模型，刻画温控系统的状态转移关系，在Simulink中建立连续层模型，刻画系统在不同运行状态下的动态性能。

步骤5 设置仿真时间、仿真步长等参数，进行故障传播过程仿真，输出仿真结果。

图3为某一条故障混杂传播路径。其中，左侧坐标是系统温度，上方曲线为温度曲线，两条虚线之间为温度控制系统正常工作的温度范围［170℃，210℃］，右侧坐标是离散状态，下方曲线为状态变化曲线。

图3 典型混杂故障传播过程

从图3可以看出，系统故障传播是在离散状态和连续温度相互作用下动态演化的。如果只将故障视为随机事件，而不考虑连续温度的实时影响，将难以准确给出故障状态的变化过程。

为了准确观察故障混杂传播过程，截取［220 h，228 h］系统温度及相应运行状态的变化，如图4中上、下两条曲线所示。

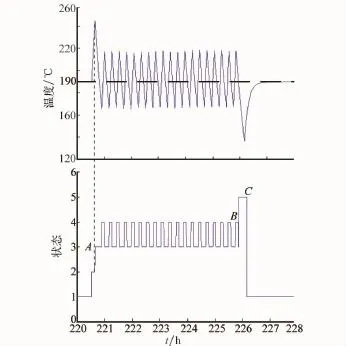
图4 ［220 h，228 h］的离散状态迁移和温度变化过程

从图4可以看出，离散故障、维修事件与连续温度之间的相互作用：

（1）220 h时系统处于正常的PI运行状态（状态1），温度稳定在190℃。

（2）之后PI控制器故障（状态2），温度急剧升高至控制器故障的检测温度240℃，检出故障（A点）。

（3）切换至开关控制器（状态3），控制温度开始下降。

（4）在开关控制器作用下，温度控制在［170℃，210℃］范围内（状态3、状态4）。

（5）在B点开关控制器也发生了故障（状态5），使温度迅速上升至控制器故障的检测温度240℃。

（6）C点开关控制器故障被检测单元检出并且PI控制器已修好，系统切换至PI控制状态（状态1）。

4 结束语

论文提出了动态系统的故障传播具有混杂特征，并初步讨论了混杂传播的建模方法。基于SHA的动态系统故障传播模型能够有效地描述不确定性因素作用下，离散单元故障和连续过程参数之间的交互作用，能更真实地描述系统故障传播过程，为动态系统故障规律认知、故障原因分析和故障诊断提供参考数据。

但在混杂传播计算过程中，离散模型采样跨度大，适合采用事件驱动机制，连续动态模型采样跨度小，适合采用时间驱动机制。离散和连续2种采样机制步长相差多个数量级，还需研究针对性的步长控制算法，通过变步长的方式来提高计算效率。

［1］Rao K D，Gopika V，Rao V S，et al．Dynamic fault tree analysis using Monte Carlo simulation in probabilistic safety assessment［J］．Reliability Engineering&System Safety，2009，94（4）：872- 883．

［2］Spackova O，Straub D．Dynamic Bayesian network for probabilistic modeling of tunnel excavation processes［J］．Computer Aided Civil and Infrastructure Engineering，2013，28（1）：1- 21.

［3］Georgilakis P S．Petri net based transformer fault diagnosis［C］∥Proc.of the IEEE International Symposium on Circuits and Systems，2004：980- 983.

［4］Srinivasan M I，Marvin K N，Alexandros V G．A Markovian dependability model with cascading failures［J］．IEEE Trans.on Computers，2009，58（9）：1238- 1249．

［5］Dobson I，Carreras B A，Newman D E．A loading-dependent model of probabilistic cascading failure［J］．Probability in the Engineering and Informational Sciences，2005，19（1）：15 -32．

［6］Kim J，Dobson I．Approximating a loading-dependent cascading failure model with a branching process［J］．IEEE Trans.on Reliability，2010，59（4）：691- 699．

［7］Van Der Schaft A T，Schumacher J M．An introduction to hybrid dynamical systems［M］．London：Springer-Verlag，2000．

［8］Seah C E，Hwang I．Stochastic linear hybrid systems：modeling，estimation，and application in air traffic control［J］．IEEE Trans.on Control Systems Technology，2009，17（3）：563- 575．

［9］Yin A，Zhao H，Zhang B．Control of hybrid electric bus based on hybrid system theory［C］∥Proc.of the International Conference on Electric Information and Control Engineering，2011：1253- 1256．

［10］Castaneda G P，Aubry J F，Brinzei N．Stochastic hybrid automata model for dynamic reliability assessment［J］．Proceedings of the Institution of Mechanical Engineers，Part O：Journal of Risk and Reliability，2011，225（1）：28- 41．

［11］Marseguerra M，Zio E．The cell-to-boundary method in Monte Carlo-based dynamic PSA［J］．Reliability Engineering&System Safety，1995，48（3）：199- 204.

Fault hybrid propagation and modeling method for dynamic system

GUO Jian-bin1，2，DU Shao-hua1，WANG Xin3，ZENG Sheng-kui1，2
（1.School of Reliability and Systems Engineering，Beihang University，Beijing 100191，China；2.Science and Technology on Reliability and Environment Engineering Laboratory，Beijing 100191，China；3.Beijing Institute of Environment Features，Beijing 100854，China）

The failure propagation in dynamic systems is driven by discrete component fault events，continuous processes as well as their interactions．This hybrid feature of the fault propagation brings about the difficulty in fault cognition and modeling．Existing researches regard faults just as discrete events．Thus they only focus on analyzing how the discrete system failures are caused by random component failures．However，the continuous processes in fault propagation have always been ignored for the sake of simplifications in engineering，which leads to the inaccuracy of the description of dynamic system failures．This paper defines the hybrid failure propagation within two dimensions for the dynamic system，and analyzes its hybrid factors and propagation features．For accurate description of these hybrid features，a hybrid failure propagation modeling method is proposed based on the hybrid theory which is used to model the interaction of discrete events and continuous processes．The proposed method is applied to a temperature control system．The simulation results show the hybrid feature of the failure propagation，as well as the feasibility of the presented modeling method．

fault propagation；hybrid；reliability；dynamic system；stochastic hybrid automata（SHA）

TB 114．3

10．3969／j．issn．1001-506X．2015．01．36

郭健彬（1979-），男，讲师，博士，主要研究方向为系统可靠性、故障机理、可靠性优化。

E-mail：guojianbin＠buaa．edu．cn

杜绍华（1987-），男，硕士研究生，主要研究方向为系统可靠性、灵敏度分析。

E-mail：h2oh2o2＠126．com

王鑫（1985-），男，工程师，硕士，主要研究方向为系统可靠性、混杂系统。

E-mail：w_xin_ok＠126．com

曾声奎（1968-），男，研究员，博士，主要研究方向为系统可靠性、故障机理、可靠性与性能一体化设计。

E-mail：zengshengkui＠buaa．edu．cn

1001-506X（2015）01-0224-05