有限次重复博弈下的网络攻击行为研究

彭伟 刘晓明 彭辉 余沛毅

近年来,各国一直在寻求一种体系对体系、多波次对多波次以及快速变化的策略集合条件下的攻防技术[1].美国人最先将博弈理论和博弈模型引入到计算机网络攻防对抗的研究之中,并产生了广泛的反响.

南加州理工大学的TEAMCORE研究小组一直致力于安全博弈领域的研究,其负责人Tambe[2]提出用Stackelberg Game Model来解决安全博弈中的一些安全防御问题,该模型也被用于网络安全领域中,取得了一定的效果.2014年,其成员Rong Yang的博士论文中用改进的随机最优响应(Quantal Response,QR)模型来建模网络对抗中人类对手行为[3−4],并用实验数据来训练行为模型以估计模型的参数,该模型在实际的网络防御中取得了良好的效果,不过该模型只适用于标准形式的博弈,即一次性的网络对抗,对多回合的网络攻防并不适用.

Camerer等长期从事博弈领域的认知模型研究,并提出一种自动调节的经验权重吸引(Experience-Weighted Attraction,EWA)学习模型[5−7],该模型综合了信念学习和强化学习的优势,在一些经典的重复博弈案例中表现出了较好的预测能力.

我国网络攻防技术研究起步较晚,博弈论用于网络攻防的研究相对国外要少一些.哈尔滨工业大学的姜伟博士[8]在2010年的博士论文中提出了一种基于攻防随机博弈模型的防御策略选取算法.该方法旨在刻画网络安全攻防矛盾动态变化,为攻防双方在多个攻防状态动态寻找最优攻防策略,不过该模型停留在算法层次上.

网络攻防博弈在很多情况下双方的较量并不是一次性的,而是多次的.所以也需要从有限次重复博弈的角度来对攻击方的行为进行建模.

在有限次重复博弈人类行为研究方面,主要采用强化学习、信念学习、EWA学习等3种学习模型.这3种模型具有各自的优缺点[9−10]:信念学习模型没有考虑自己的策略行动对其他参与者的影响,因而不能较好地反映重复博弈的动态过程;强化模型只是简单地对成功或者失败的经验进行强化,没有考虑未被采用的策略,适应性稍差;EWA学习模型则考虑了过去成功和失败经验对博弈决策的影响.

1 网络攻防的策略分析

1.1 攻击者的策略分析

攻击者可以选择多种策略进行攻击,通常的攻击策略有如下几种:

1)Speed,攻击者希望快速攻击使得自己迅速得手,即在防御者发现或作出反应之前就取得成功.

2)Stealth:攻击者选择隐藏自己避免被发现.

3)Deception:攻击者欺骗防御者,使得防御者在错误防御中浪费资源.

4)Random:用随机方式进行攻击.

5)Least resistance:攻击者用最简单经济的方式攻击.

1.2 防御者的策略分析

防御者在防御过程中采取的策略如下:

1)Dissuasion:采取劝说的方法.

2)Prevention:建立虚假资源防止攻击者攻击或诱骗攻击者攻击无价值的目标.

3)Prevention:防御者建立防护体系来预防攻击.

4)Repair:通过检测发现系统中的漏洞,采取修复的方法来降低风险.

5)Exploitation:判定攻击方的防御是否存在漏洞,从防御转为主动攻击.

在网络攻防的过程中,假定我方是防御者,那么如何能够正确地预见攻击者未来可能的行为在网络防御中变得非常重要,下面将重点讨论攻击者行为模型的构建.

2 攻击者的行为分析

国外的学者在标准形式的博弈(一次性博弈)中对人的理性进行了分级[11].本文在理性分级的基础上,对网络攻击者再次进行划分,即追求长远利益的攻击者和追求短期利益的攻击者.按照这两个原则划分后,实际上可以将攻击者分为4类.从直觉上来说,这4类攻击者的行为模型应该是有差别的,因此,需要正确地对这4类人进行建模.

将攻击者分成4类,分别构建4类攻击者的决策行为模型.具体如下:

1)对于思考等级低且追求长期利益的攻击者(长远近视攻击者),这类攻击者不仅会根据过去的历史经验来学习,也会把未来的因素考虑到其中,因此借鉴EWA学习方法来建模.

2)对于思考等级高且追求长期利益的攻击者(长远老练攻击者),这类攻击者被称之为Sophistication,他们有教授(Teaching)的能力,能够引导和带动其他参与者进行学习,因此,建立这类攻击者的行为模型时应考虑他们的Teaching能力.

3)对于思考等级低且追求短期利益的攻击者(短期近视攻击者),借鉴增强学习的方法来建模,即这类攻击者只会根据过去的历史经验来学习和做决策.

4)对于思考等级高且追求短期利益的攻击者(短期老练攻击者),运用随机最优响应均衡(Quantal Response Equilibrium,QRE)[11−12]的相关理论来进行建模.

3 攻击者行为模型的构建

根据上面的分类,假定短期者的比例为s,短期老练者的比例为sp,那么短期近视者的比例为s(1−p);同理假设长远者的比例为1−s,那么长远老练者的比例为(1−s)q,则长远近视者的比例为(1−s)(1−q).

其他符号说明:

λLM:长远近视攻击者的理性级别;

λLS:长远老练攻击者的理性级别;

λSM:短期近视攻击者的理性级别;

λSS:短期老练攻击者的理性级别;

其中λLM,λLS,λSM,λSS的取值在(0,+∞)之间,值越大,代表理性级别越高.

假设目前攻防双方所处的轮次为t轮,那么需要重点求解在t+1轮,各种类型的攻击者会采用什么样的策略.

3.1 长远近视攻击者的行为模型

长远近视攻击者不仅会根据过去的历史经验来学习,也会把未来的因素考虑到其中,因此,本文借鉴了Ho,Camerer和Chong等人提出的EWA模型[5].

EWA学习模型的基本思路:假设有n个博弈参与者,参与者用i来表示,i=1,2,···n.参与者i有mi种策略,其策略空间用Si,即是个体策略空间组成的博弈策略空间,第i个参与者第k个策略(用表示)的初始魅力值为(0),参与者和其他博弈参与者在t时期选择的策略分别为si(t)和s−i(t),参与者i选择策略si(t)的收益值为πi((t)),其第k个策略t时期魅力值为(t),t时期的经验权重为N(t),(t)和N(t)都是随着时间发生变化(或更新).t时期的策略魅力值(t)是由上一期经验权重N(t−1)和选择策略的当期收益值πi((t))来负责更新.Camerer等人将策略魅力值的(t)和经验权重的更新方程构建如下:

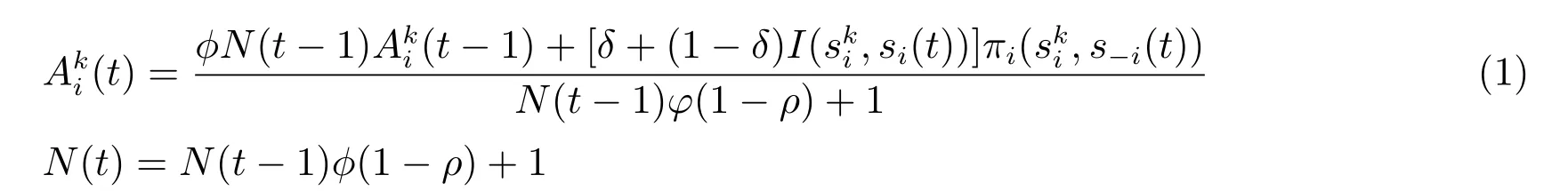
其中,φ是魅力值衰退系数,博弈中随着对手、环境不同或者遗忘等原因导致策略的有效性下降.φ在0∼1之间取值.

I(.)是指标函数,取值为1或者0,如果si(t)和相等,则I取值为1,反之为0.

δ是被放弃收益的权重,δ取值在0～1之间.

ρ是魅力值增长控制系数,模型用ρ表示不同模型对博弈学习过程策略魅力值增长的影响.ρ取值在0∼1之间.

在网络攻防博弈中,参与博弈的实际上只有两方,即攻击者和防御者,现在我们重点要求的是攻击者的可能策略.攻击者选取的策略为上文中列出的5种(甚至更多)之一.φ,δ,ρ的取值根据实际的案例来确定.在完成魅力值的计算以后,还需要确定攻击者在t+1轮究竟选取哪种攻击策略.此时,可以根据logit规则来确定,即:

式(2)给出了攻击者各种策略的选择概率,在实际应用时策略的选择根据各种策略的选择概率而确定,通常是概率越大,选择的概率越高.下面其他3个模型类似.

3.2 长远老练攻击者的行为模型

长远老练攻击者会将剩下轮次中的总收益最大化,这也是他们跟短期老练攻击者的显著区别.

攻击者i选择k策略的收益结构如下:

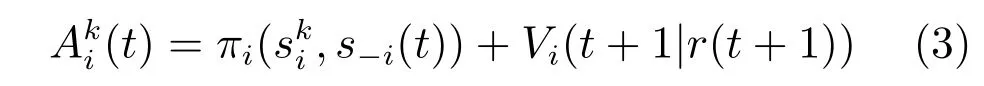
Vi(t+1|r(t+1))代表博弈过程中t+1轮次后所有剩下轮次的预先估计值(基于防御者的后验信念来确定的).其值可以根据下列公式来确定.

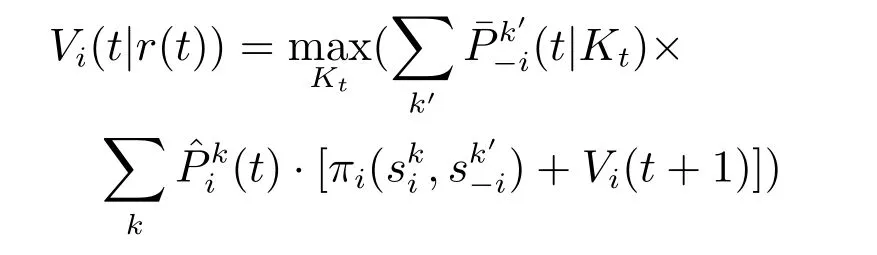
其中,Kt≡{kt,kt+1,···,kT}.

最终,攻击者各种策略的选择概率由下列公式来确定:

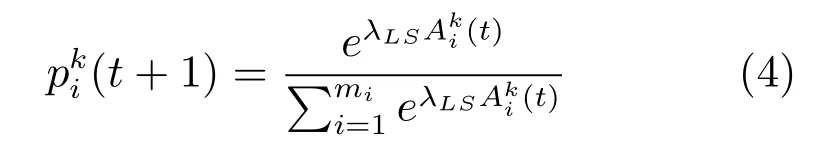
3.3 短期近视攻击者的行为模型

这类攻击者的特点是根据过去的历史经验来学习,因此,采用自适应的学习模型比较合适.对于这类攻击者,其策略主要是根据前面多轮次的经验来选择的,因此,可以采用强化学习模型.实际的模型以3.1节的模型为基础,当δ=0,ρ=1,N(0)=1时,EWA模型退化为强化学习模型.此时,

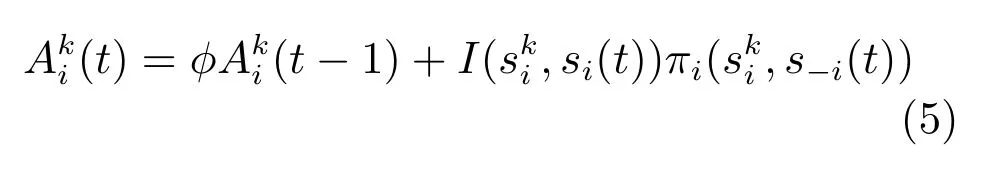
在此基础上,攻击者的策略选择依然是以logit规则来确定,即:

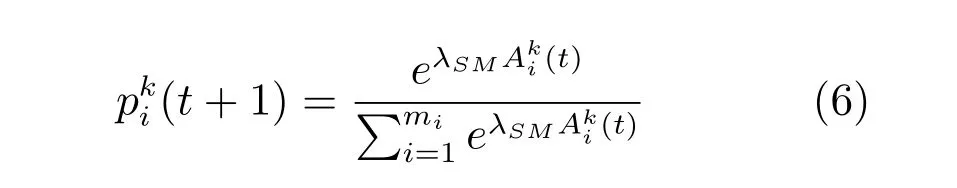
3.4 短期老练攻击者的行为模型

短期老练攻击者会追求短期内的最高收益,因此,其攻击行为模型可以参考QRE来建立.其策略选择模型如下:

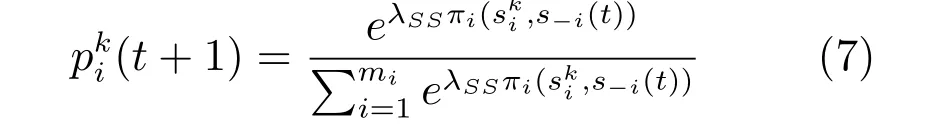
其中πi((t))代表第i个攻击者选择k策略时的收益值.

以上4个行为模型都是根据logit规则给出的,如果(t+1)的值越大,那么说明攻击者i在第t+1轮选择k策略的概率就越高.

4 参数估计

λLM,λLS,λSM,λSS分别代表各种类型攻击者的理性级别,根据先前的假设,老练攻击者的理性级别比近视攻击者的理性级别高;长远攻击者比短期攻击者的理性级别高.在观察和分析200次的实际网络攻防中网络攻击者的攻击行为数据之后,我们给出的估计是λLS和λSS在(2.5,4)之间,λLM和λSM在(0.5,2)之间.

根据200次实际攻防数据的统计分析,大致估算出短期攻击者的比例为70%−80%,长期攻击者的比例为20%−30%.4种类型攻击者的实际比例如下:

1)短期近视攻击者的比例为50%∼60%;

2)短期老练攻击者的比例为15%∼25%;

3)长期近视攻击者的比例为15%∼20%;

4)长期老练攻击者的比例为4%∼9%.

φ,δ,ρ的取值跟具体的应用案例有关系,在本文的试验中φ取0.2,δ取0.25,ρ取0.7.

5 试验分析

我们用另外100组实际网络攻防的数据对建立的行为模型进行了分析,比较对象是单纯的QRE模型和强化学习(Reinforcement Learning,RL)模型,分别比较了在博弈多次之后的预测准度.

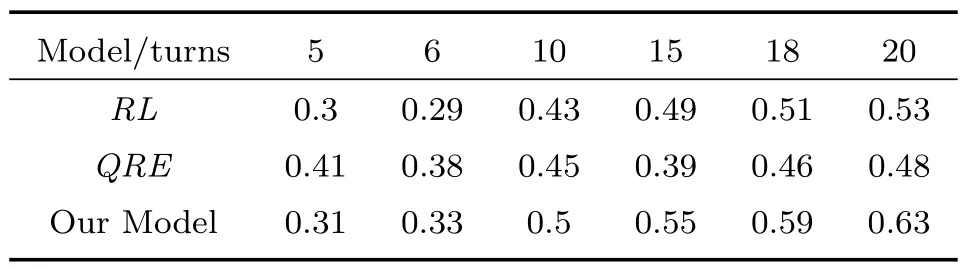
表1 3种行为模型的预测准确度对比

根据表1的试验数据,当博弈的轮次比较小的时候,QRE的预测准度比较高,但是随着轮次的增加,QRE的准度并没有明显增加;强化学习和我们的行为模型在博弈轮次较低时,预测准度稍低,随着博弈次数的增加,预测准度也增大,我们给出的行为模型在博弈次数到10次以后,预测准度要明显的高于强化学习模型.

6 结论

本文所构建的攻击者行为模型比较适合博弈轮次比较多的情况.实际的网络攻防博弈过程中,作为防御者而言,对手究竟是哪种类型的攻击者一开始并不明确,因为敌在暗处.在实际运用时,可以根据之前设定的比例来假定攻击者属于哪种类型.由于初始判断不一定准确,在最前面的几轮博弈中可能会产生一些误差,为了提高效率,还可以采用其他方法,比如声誉模型等,根据前几轮攻击者的攻击特点来判断攻击者的真实类型,从而更有效地提高预测的准度.