基于非下采样剪切波变换域方向信息测度的多聚焦图像融合方法

2015-06-19邢雅琼王晓丹梁兵杰

系统工程与电子技术 2015年1期

关键词：纹理方向系数

邢雅琼，王晓丹，梁兵杰，秦卓

（1．空军工程大学防空反导学院，陕西西安710051；

2．大唐移动通信设备有限公司西安分公司，陕西西安710061）

基于非下采样剪切波变换域方向信息测度的多聚焦图像融合方法

邢雅琼1，王晓丹1，梁兵杰2，秦卓2

（1．空军工程大学防空反导学院，陕西西安710051；

2．大唐移动通信设备有限公司西安分公司，陕西西安710061）

根据非下采样剪切波变换（non-subsample shearlet transform，NSST）在图像融合领域的优势和多聚焦图像的成像特点，将NSST运用于多聚焦图像融合。在NSST变换域中，利用方向信息测度能够突出图像边缘纹理特征以及降低图像噪声，将其运用在高频子带系数的融合规则中，并对传统的低频融合策略进行改进，将低频系数和高频系数的融合图像进行NSST的逆变换，得到融合图像。计算机仿真实验表明，相比于传统的剪切波变换的融合策略，本文提出的图像融合方法提高了图像的融合质量，增加了图像的信息量，并能降低图像噪声，具有一定的有效性和实用性。

图像融合；非下采样剪切波变换；方向信息测度

0 引言

图像融合［1］是指综合不同传感器所获得的两幅或多幅原图像中的主要信息，使融合图像能够更加准确、清晰、可靠地表达图像信息。多聚焦图像是传感器感知场景内同时存在与镜头距离不同的多个目标时，因无法同时聚焦这些目标而借助同一传感器多次成像或多个同质传感器一次成像得到的聚焦不同的多幅图像或图像序列［2］。将多聚焦图像序列中的聚焦部分融合在一幅图像中，使其完整清晰地呈现在一幅图像中是多聚焦图像融合的主要目标。

近年来，多尺度变换已成为图像融合领域的研究热点，而小波变换的提出是多尺度变换的里程碑［3］。小波变换可以有效地处理一维或者高维信号的点奇异性问题，但对于图像的“线奇异性”问题，小波变换却无法捕捉。为了解决这一问题，曲波变换［4］和轮廓波变换［5］被相继提出，这两种变换在多尺度变换的基础上对图像进行多方向分解，且二者的基函数都具有楔形或矩形支持区，从而为图像的高维奇异性提供了更优的稀疏表达方式，但是这两种方法在多尺度分解和多方向分解过程中的下采样操作会使其不具备平移不变性，从而使得融合图像中可能出现Gibbs现象。为了解决这一问题，具有平移不变性的非下采样轮廓波变换（non-subsample contourlet transform，NSCT）［6-7］被提出，该方法可以更好地稀疏表达图像，且具有良好的时频特性和平移不变性，但由于NSCT分解的方向数有限，其对于细节信息的提取并非无懈可击，因此，无方向数限制的非下采样剪切波变换（non-subsample shearlet transform，NSST）应运而生。NSST是由多尺度滤波器和多方向滤波器构成的，由于其方向滤波器的支撑区域较小，从而减小了Gibbs现象发生的概率并提高了计算效率［8］。在图像融合领域，具有平移不变性的NSST可以有效提高融合图像质量和融合效率。

经过NSST的多尺度多方向分解，多聚焦图像被分解为一个低频图像和若干个高频图像，低频图像是原图像的近似图像，包含了原图像的轮廓信息，而高频图像中包含有图像的边缘、纹理等重要的细节信息。因此，在NSST变换域中，高频图像融合规则的选择直接影响到原图像的融合效果。根据NSST分解后高频图像的特点，本文采用了一种基于方向信息测度的图像融合规则。根据方向信息测度［9］能够突出图像的边缘纹理等重要信息的优点，判断出高频图像中边缘点及纹理点所在的位置，从而有效地提取出高频图像的边缘及纹理信息，并将其注入到融合图像中，增加融合图像的信息量和清晰度。此外，由于图像的方向信息测度对于噪声的不敏感性，将方向信息测度引入到高频图像的融合策略中，可以减少噪声对图像融合性能的干扰。

1 图像的NSST变换

剪切波的方向滤波是在多维和多方向情况下的自然扩展［10］，剪切波可以将这些再生函数的集合表达为

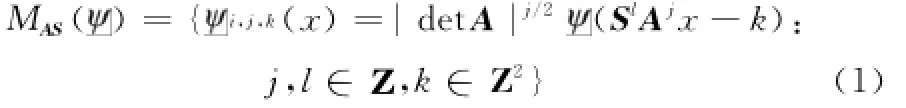
在L2（R2）域中，基函数i，j，k（x）的集合是通过对单个局部特性良好的窗函数进行旋转、剪切及平移变换操作而形成的，这些集合共同构成了Parseval框架，这个过程构成了仿射系统。当维数n＝2时，∈L2（R2），A和S均为2×2维的可逆矩阵，矩阵A决定图像的多尺度分解，是具有“各向异性”的膨胀矩阵；剪切矩阵S决定图像的多方向分解，且|det S|＝1；j表示分解尺度；l表示方向参数；k表示平移参数。当MAS（）具有紧框架，MAS（）的元素称为合成小波，A和S的表达式分别为A＝［a 0 0 a1／2］，S＝［1 s 0 1］，此时的合成小波即为剪切波，通常取a＝4，s＝1，即A＝［4 0 0 2］，S＝［1 1 0 1］［11］。

NSST在NSCT的基础上进行了改进，NSST的变换过程也是由多尺度分解和多方向分解两部分组成。NSST的多尺度分解和NSCT相同，均采用了非下采样金字塔分解（non-subsample pyramid，NSP）。图像经过k级NSP多尺度分解，会得到k＋1个子带图像，包括一个低频图像和k个大小与原图像相同，但尺度不相同的高频图像。但NSST在方向分解中摒弃了NSCT中的方向滤波器，采用了Shear滤波器，Shear滤波器分解的核心思想是在伪极网格上对图像进行二维傅里叶变换［12］，然后在网格上用一维子带滤波器进行滤波，整个过程不需要对原图像进行临界采样操作，从而保证了方向滤波过程中不会出现图像失真现象，此外还保证了图像的平移不变性，并有效避免了Gibbs现象。由于NSST的方向滤波器可以通过一个矩阵形式的窗函数表示，且区间内的长宽比可随尺度变化而变化［13］，并且可以根据时间复杂度的需要和融合质量的要求决定方向数的多少，从而解决了NSCT的非下采样方向滤波器（non-subsample directional filter bands，NSDFB）所存在的方向数的限制问题。因此，NSST不仅保留了NSCT的局部时频特性和平移不变性，而且比NSCT更具有灵活性和有效性［14］。对经过多尺度分解的子带图像进行l级多方向分解，得到2l＋2个与原图像大小相同的方向子带图像。图1是原图像及经过NSST变换分解后的低频图像和高频图像，图2是NSST的分解过程示意图，图3中灰色阴影部分是NSST中方向分解的支撑基。

2 图像的方向信息测度

边缘和纹理信息是图像融合中至关重要的细节信息，提取原图像中的边缘、纹理等细节信息并注入到最后的融合图像中是图像融合的目标所在。通过计算像元灰度值的方向信息测度可以判断出该像素点是否属于图像的边缘或纹理信息，像素点的方向信息测度值越大，则该点位于图像的边缘或纹理点的可能性会越高。此外，文献［9］也多次提及图像的方向信息测度可以将图像的边缘纹理信息和噪声分离开，更好地将原图像中的有用信息提取出来，有效地降低了噪声对融合效果的影响。

设图像X在（i，j）处的像素灰度值为p（i，j），r为以（i，j）为中心的邻域半径，则以（i，j）为中心的邻域为

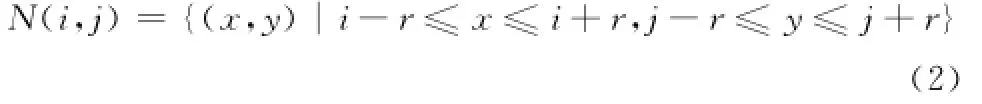
若用lθ表示过邻域中心点（i，j）的一条直线，其角度为θ，则lθ可以将邻域窗口N分成两部分，即NL和N H。则方向信息测度为

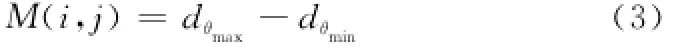
其中

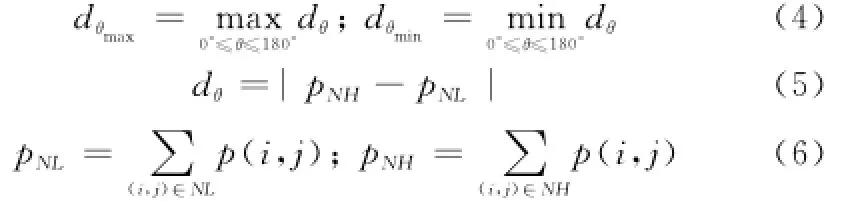
图1 两层NSST分解示意图

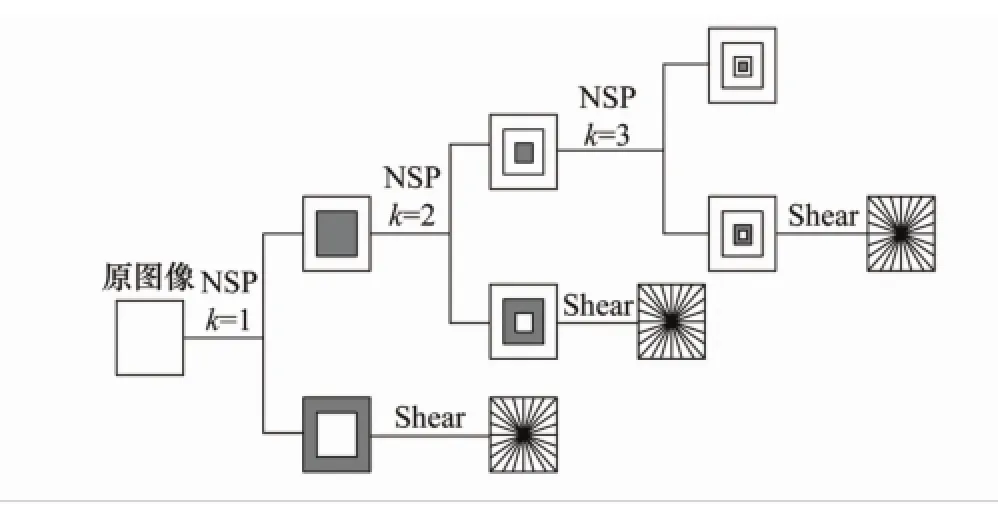
图2 NSST的分解过程

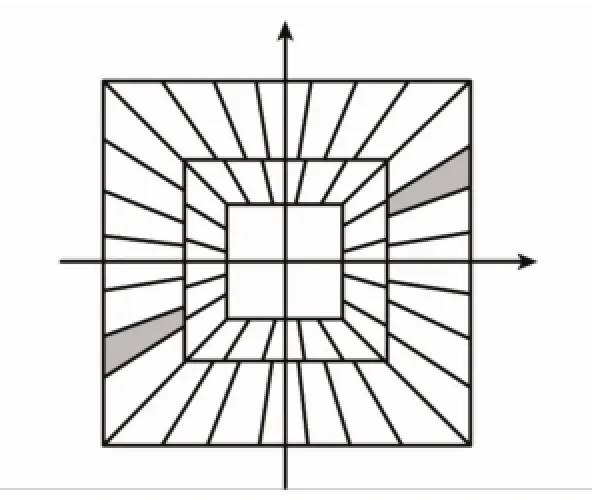
图3 NSST变换后的频域

图4 （a）表示方向信息测度的基本框架，图4（b）为Came图片，图4（c）为图4（b）的方向信息测度。

3 基于NSST域方向信息测度的多聚焦图像融合算法

根据多聚焦图像的成像机理，多聚焦图像的聚焦部分包含了清晰的边缘纹理细节信息，但其他部分较为模糊，对于同一场景不同聚焦的图像，如何将他们的互补信息融合起来，构成高质量的融合图像是需要研究的问题。而基于NSST域方向信息测度的多聚焦图像融合算法可以较好地解决这一问题。

原图像经过NSST分解，会得到一幅低频图像和若干幅与原图像大小相等的高频图像。经过NSST多级分解后的高频图像中含有原图像的结构、边缘、纹理等重要信息，而这些信息往往体现为像素点方向信息的变化。因此对高频信息采用基于方向信息测度的融合方法，利用像素点方向信息测度来判断该点是否属于图像的边缘点或纹理点，一方面提高了高频图像中高能量区域细节信息的表达，另一方面更优地提取了高频图像中信息量较小的平滑区域的特征信息，从而大大提高了高频图像的融合质量。对于具有与原图像相似信息的低频图像，传统的绝对值取大法会丢失原图像中的许多信息，因此本文采用基于标准差的加权平均法对低频图像进行融合。基于NSST域方向信息测度的多聚焦图像融合算法如下：

输入：经过配准的多聚焦图像A和B

输出：经过本文方法得到的多聚焦图像的融合图像F

图4 图像的方向信息测度

步骤1 对多聚焦图像A和B分别利用NSST变换进行多尺度多方向分解，并将分解后的低频系数分别定义为和，高频系数定义为和B，其中，k为图像的分解尺度，l为k级尺度下图像的多方向分解级数；

步骤4 对低通系数Flow和高频系数进行NSST逆变换，从而得到最终的融合图像F。

3.1 低频子带系数的融合策略

前文中提到，经过NSST分解后的低频图像是原图像的近似图像，包含了原图像中的能量信息。传统的低频图像融合策略是采用平均值的融合规则，这种系数选择的方法会降低融合图像的对比度，并损失部分能量信息。因此，对于低频图像和B的融合，本文采用基于标准差（standard deviation，SD）的0系数选择规则。

SD描述了各像素灰度值与平均灰度值的离散程度，如果用p（i，j）表示像元（i，j）处的灰度值，M×N表示图像大小，则SD的计算方法为

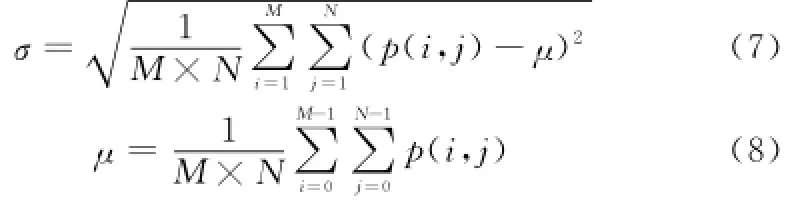
由于SD越大，灰度值越离散，图像则包含更多的信息，所以采用基于SD的加权平均融合规则对NSST域的低频图像进行融合。首先根据式（7）和式（8）计算两幅低频图像的SD和平均值，然后按照以下方法对图像进行融合：

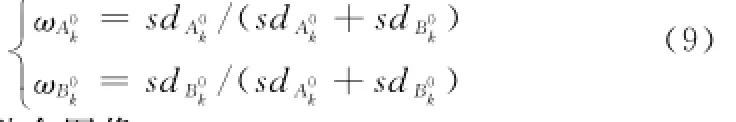
从而获得低通融合图像

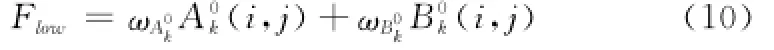
3.2 高频子带系数的选择

在NSST域中，高频图像中的边缘细节信息常常存在于灰度值模值较大的像素中，因此，传统高频图像的融合方法都是采用绝对值取大的融合策略，但是这种融合策略不能很好地提取出高频图像中的低频信息，从而影响了图像的融合性能。因此，本文利用图像的方向信息测度设计了新的系数选择方案，可以更好地表达图像的边缘纹理信息，且能有效去噪。

图像梯度能量（energy of graident，EOG）是图像的梯度信息，具有表现图像聚焦特性和清晰度的能力［15］

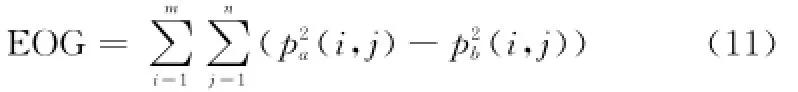
式中

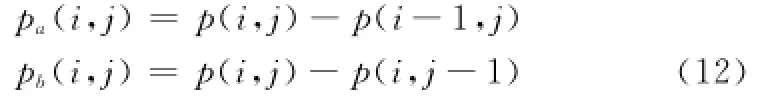
其中，p（i，j）表示像元（i，j）点的灰度值。若图像的局部区域大小为N×N，那么局部区域的梯度能量则为

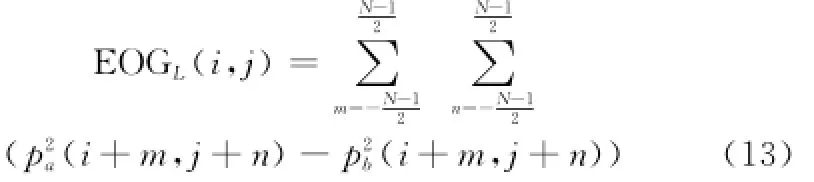
为了进一步提高高频图像的融合质量，更好地表达图像在局部区域内的聚焦特性和清晰度，在高频图像的融合中引入方向信息测度梯度能量的图像融合方法，其定义为

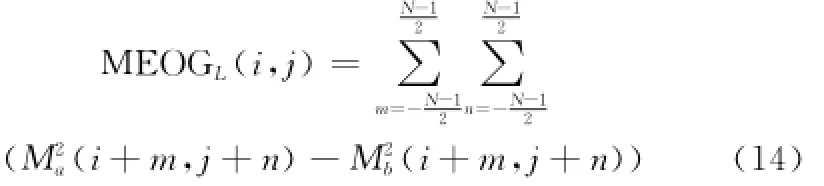
式中，MEOGL（i，j）表示点（i，j）处的方向信息测度的梯度能量；M（i，j）表示点（i，j）处的方向信息测度值，M（i，j）可以根据式（3）计算。由于点（i，j）的局部梯度能量越大，所表征的边缘纹理的清晰度越高，所以根据式（10），高频图像的系数选择方案可定义为

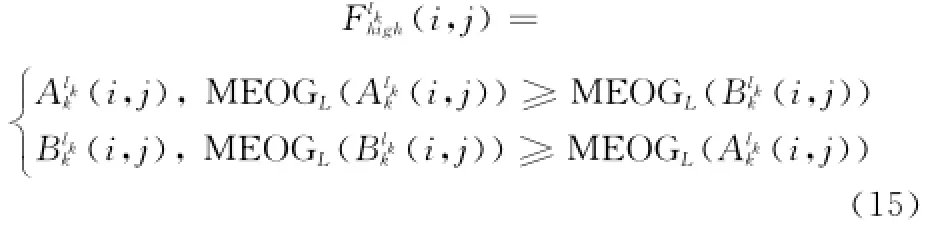
4 仿真实验

4.1 无噪声图像融合实验

4.1.1 实验说明

根据以上所述的理论及方法，本文以Matlab2010为工具，选择了两组灰度级为256×256的无噪声多聚焦图像进行仿真实验和分析，第一组是Bottle的多聚焦图像，第二组为Vegetable的多聚焦图片，两组图片都已经过配准。此外，为了进一步证明本文方法的有效性，共设计了4种算法与本文方法进行比较：

方法1 在时域中对图像进行轮廓波变换（contourlet transform，CT），在CT域中，图像低频系数采用传统的取平均值的融合规则；高频系数采用传统的绝对值取大的融合规则。

方法2 在时域中对图像进行NSCT分解，对分解后的低频系数继续采用取平均值的融合规则；高频系数采用传统的绝对值取大的融合规则。

方法3 在时域中以NSST作为分解工具，在频域中采用和方法1、方法2相同的融合规则，从而验证NSST相对于CT和NSCT在多聚焦图像融合中的优势。

方法4 对NSST分解后的图像低频系数采用本文提出的低频子带系数的选择规则；对高频系数继续采用传统的绝对值取大的融合规则，用以验证本文低频系数融合规则的有效性。

需要说明的是，CT、NSCT和NSST的分解级数均为4级，本文采用的高频系数选择规则中，邻域大小为3×3。

图像融合质量可以从主观和客观两个方面进行比较，主观评价通常经过目视或目测来进行，一般是指对图像亮度、纹理、对比度以及清晰度的评价。而客观评价标准是指对图像定量的分析，本文所采用的客观评价标准是SD、信息熵（information entropy，IE）、平均梯度（average gradient，AG）以及文献［16- 17］中提到的边缘信息保留量（QAB／F）。其中，SD也称为均方差，它可以反映图像各个像元灰度相对于灰度平均值的离散情况，SD越大，图像的反差越大，可看到的信息越多，图像质量越好。IE是从信息论角度反映影像信息丰富程度的一种度量方法，IE的大小反映了图像携带的信息量的多少，因此，影像的IE越大，其信息量就越丰富，质量也就越好［18］。AG能够反映出图像对微小细节反差的表达能力，一般来说AG越大，表明影像越清晰。QAB／F的取值一般位于0～1，其取值越大，说明原图像的边缘等重要细节信息在融合图像中的存在量越大，那么融合图像的质量则越高。

4．1．2 实验结果及分析

图5为Bottle多聚焦图片的图像融合结果，对于Bottle多聚焦图像融合结果，如果从主观评价的角度来看，不难看到，方法4和本文方法的融合图像其对比度和亮度均优于其他3种方法，方法1的清晰度较差，方法2和方法3从视觉上来看区别并不大，方法3的清晰度略优于方法2的融合图像清晰度。由于主观分析存在一定局限性，因此对Bottle图像融合结果进行客观评价，表1为客观评价的分析结果。根据表1中的数据可以看到，本文方法在SD、IE、AG以及QAB／F4项指标中均优于其他4种方法。其中，方法3的4项数据均高于方法1和方法2的4项评价结果，说明NSST分解在多聚焦图像融合领域中优于CT和NSCT分解。而方法4的各项指数均高出方法3，证明本文采用的低频系数选择方案可以使融合图像的对比度、清晰度以及信息量得到提升。同样地，本文方法在QAB／F指标中远高于其他4种方法，进一步说明本文方法可以更好地将原图像中的边缘纹理信息提取出来并融入到融合图像中。此外，本文方法的融合图像SD和AG远高于其他4种方法，说明本文所采用的图像融合方法可以提高多聚焦图像的融合性能。

图5 Bottle图像融合实验结果

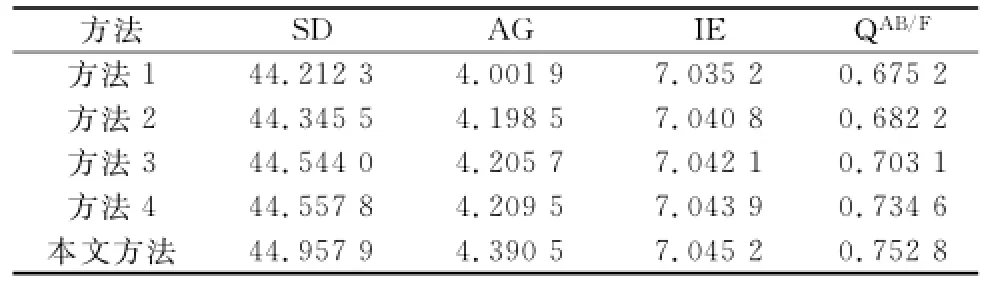
表1 图像Bottle的融合结果客观比较

图6为Vegetable多聚焦图片的图像融合结果。从主观评价角度看，依然是方法4和本文方法的融合图像具有较佳的清晰度和亮度；方法3的融合质量略高于方法1和方法2；方法1和方法2的融合图像从主观上看依然是较为相似。同样地，为了进一步对图像融合质量进行评估，需要对融合图像进行客观分析，表2即为对Vegetable多聚焦图像融合结果的客观分析。根据表2中的数据，依然是方法4和本文方法的各项指标表现较好，方法3的各项指标优于方法1和方法2。说明对于不同的多聚焦图像，在NSST域中图像的融合效果依然优于CT和NSCT，此外，也再次证明了本文方法在不同的图像环境中均具有良好的融合性能。

图6 Vegetable图像融合实验结果

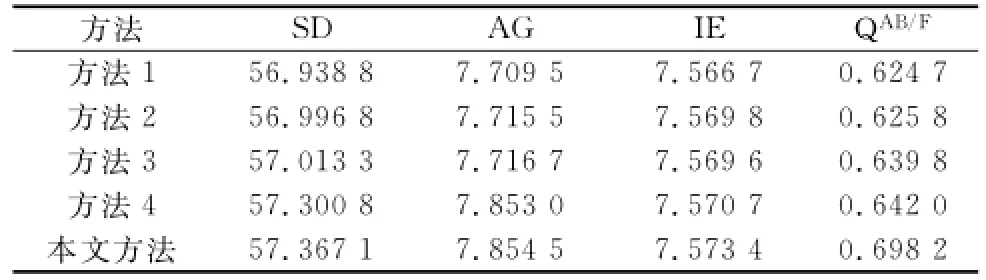
表2 图像Vegetable的融合结果客观比较

4.2 带噪声图像融合实验

4．2．1 实验说明

为了进一步证明本文方法可以有效地将原图像的有用信息和噪声分离开，选取两组带有高斯白噪声的256×256灰度级的多聚焦图像进行图像融合的对比实验，一组为Came多聚焦图像，另一组为Lab多聚焦图像，并继续采用第4．1节设计的4种图像融合方法以及本文方法来完成图像的对比实验。

对于带噪图像的融合结果，依然从主观和客观两个角度对融合结果进行评价。不同的是，在带噪图像的融合实验中，采用的客观评价标准为互信息（mutual information， MI）和峰值信噪比（peak signal to noise ration，PSNR）。MI的计算结果可以显示出融合图像从原图像中吸取的信息量的多少，一般来讲，从原图像中吸取的信息量越大，融合图像的融合质量越好［19］。而PSNR值则表示了图像中噪声含量的多少，如果计算无噪声原图像的标准图像和各方法融合图像之间的PSNR，PSNR值越大，表明其噪声越小，这样就可以分析出各种融合方法是否具有去噪的性能。

4．2．2 实验结果及分析

图8和图9分别是图7所示的带噪声的Came图像和Lab图像的融合实验结果。从主观角度来看，各个方法对于不同的图像均能将原图像中的信息提取出来，并融入到最终的融合图像中。但在两组实验中，本文方法的融合图像其清晰度均优于其他4种方法的融合图像；方法1和方法2的融合图像差别并不大，但两组实验的方法3的融合图像在亮度和清晰度上均优于方法1和方法2。因此，从主观上讲，NSST分解在多聚焦图像融合中优于CT和NSCT分解，且本文设计的融合规则对于图像融合及去噪都具有一定意义。

图7 带噪声的多聚焦图像

图8 Came图像的融合实验结果

图9 Lab图像的融合实验结果

从表3和表4的客观分析来看，在两组实验中，方法3、方法4以及本文方法在两项评价指标中的表现明显优于方法1和方法2，说明NSST分解不仅能够更好地提取原图像中的有用信息并注入到融合图像中，且在图像去噪方面也具有一定优势。此外，本文方法的各项指标在两组实验中也优于方法3和方法4，从而再次说明本文所采用的低频系数融合规则以及高频系数融合规则在多聚焦图像融合中具有良好的融合性能。

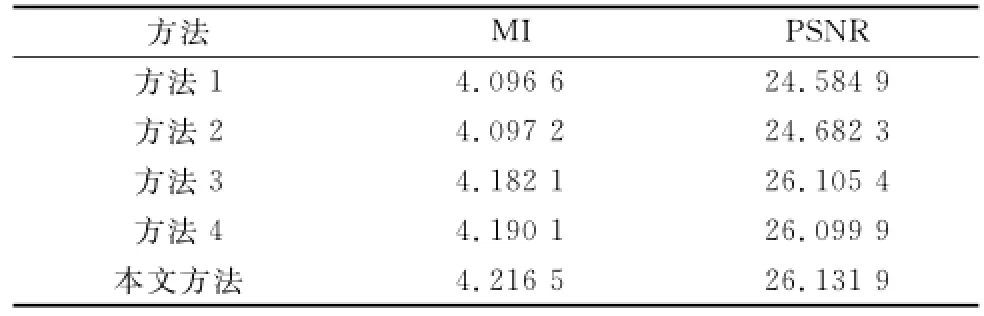
表3 图像Came的融合结果客观比较

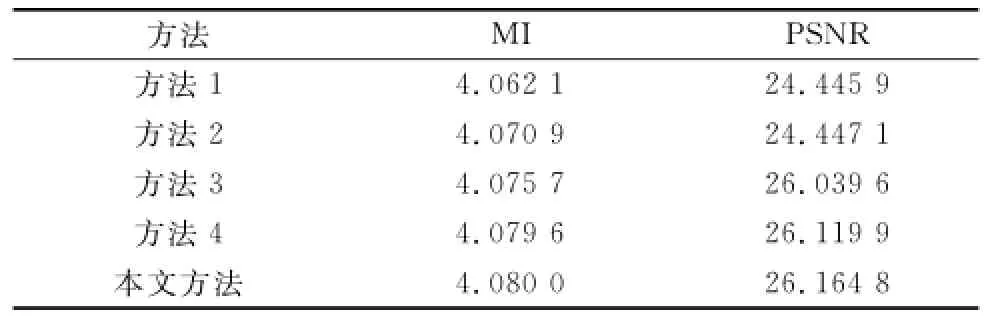
表4 图像Lab的融合结果客观比较

5 总结

本文根据NSST在图像融合领域中的优势以及多聚焦图像的成像特征，将NSST运用到多聚焦图像融合领域，并根据NSST中高频系数和低频系数的特点，对低频系数采用基于SD的融合规则，并对高频系数采用了基于方向信息测度梯度能量的图像融合策略。实验表明，基于本文方法的多聚焦图像融合不仅可以使融合图像更好地表达出原图像中的边缘、纹理和结构特征，还能够降低带噪图像融合中融合图像的噪声，从而提高了多聚焦图像的融合性能。如何进一步改进算法以提高运算速率是下一步工作的重点。

［1］Jing Z L，Xiao G，Li Z H．Image fusion-theory and applications［M］．Beijing：Higher Education Press，2007：1- 3．（敬忠良，肖刚，李振华．图像融合—理论与应用［M］．北京：高等教育出版社，2007：1- 3．）

［2］Ma M，Wan R Y，Yin Y L．Multi focus image fusion based on grey relation of similarity in curvelet domain［J］．Acat Electronical Sinica，2012，40（10）：1986- 1988．（马苗，万仁远，尹义龙．基于相似性灰关联的Curvelet域多聚焦图像融合［J］．电子学报，2012，40（10）：1986- 1988．）

［3］Shivamurti M，Narasimhan S V．A dual tree complex discrete cosine harmonic wavelet transform（ADCHWT）and its application to signal／image denoising［J］．Journal of Signal and Information Processing，2012，2（3）：466- 475．

［4］Candès E J，Donoho D L．New tight frames of curvelets and optimal representations of objects with piece wise C2 singularities［J］．Communicationon Pure and Applied Mathematics，2004，57（2）：219- 266．

［5］Do M N，Vetterli M．The contourlet transform：an efficient directional multiresolution image representation［J］．IEEE Trans. on Image Processing，2005，14（12）：2091- 2106．

［6］Zhou J P，Cunha A L，Do M N．Nonsubsampled contourlet transform：construction and application in enhancement［C］∥Proc.of the IEEE Conference on Image Processing，2005：469- 472．

［7］Cunha A L，Zhou J P，Do M N．The nonsubsampled contourlet transform：theory，design and applications［J］．IEEE Trans.on Image Processing，2006，15（10）：3089- 3101．

［8］Shi C．Research on image fusion algorithm based on shearlet［D］．Xi’an：Xidian University，2012．（石程．基于Shearlet的图像融合方法研究［D］．西安：西安电子科技大学，2012．）

［9］Li H F．Research on pixel level fusion methods for multifocus image［D］．Chongqing：Chongqing University，2012．（李华锋．多聚焦图像像素级融合方法研［D］．重庆：重庆大学，2012．）

［10］Kong W W，Lei Y J．Technique for image fusion based on NSST domain and human visual characteristics［J］．Journal of Harbin Engineering University，2013，34（6）：777- 782．（孔韦韦，雷英杰．基于NSST域人眼视觉特性的图像融合方法［J］．哈尔滨工程大学学报，2013，34（6）：777- 782．）

［11］Lim W Q．Nonseparable shearlet tranform［J］．IEEE Trans. on Image Processing，2013，22（5）：2056- 2065．

［12］Geng P，Wang Z Y，Zhang Z G，et al．Image fusion by pulse couple neural network with shearlet［J］．Optical Engineering，2012，51（6）：1- 8．

［13］Shi C，Miao Q G，Xu P F．A novel algorithm of image fusion based on shearlets and PCNN［J］．Neurocomputing，2013，117（10）：47- 53.

［14］Liu J H，Yang J G，Li B Z．Multi-focus image fusion by SML

in the shearlet subbands［J］．TEL KOMNIKA Indonesian Journal of Electrical Engineering，2014，12（1）：618- 626．

［15］Zhang Q，Guo B L．Fusion multi-focus image based on nonsubsample contourlet transform［J］．Acta Automatica Sinica，2008，34（2）：136- 141．（张强，郭宝龙．基于非采样contourlet变换多传感器图像融合算法［J］．自动化学报，2008，34（2）：136- 141．）

［16］Xydeas C，Petrovic V．Objective image fusion performance measures［J］．Electronics Letters，2000，36（4）：308- 309．

［17］Petrovic V，Xydeas C．Sensor noise effects on signal-level image fusion performance［J］．Information Fusion，2003，4（3）：167- 183．

［18］Kong W W，Lei Y J，Lei Y，et al．Fusion technology for gray-scale visible light and infrared images based on improved NSCT［J］．Control and Decision，2010，25（11）：1665- 1669．（孔韦韦，雷英杰，雷阳，等．基于改进型NSCT变换的灰度可见光与红外图像融合方法［J］．控制与决策，2010，25（11）：1665- 1669．）

［19］Zheng H，Zheng C，Yan X S，et al．Visible and infrared image fusion algorithm based on shearlet transform［J］．Chinese Journal of Scientific Instrument，2012，33（7）：1614- 1619．（郑红，郑晨，闫秀生，等．基于剪切波变换的可见光与红外图像融合算法［J］．仪器仪表学报，2012，33（7）：1614- 1619．）

Fusion technique for multi-focus images based on orientation information measurement in non-subsample shearlet transform domain

XING Ya-qiong1，WANG Xiao-dan1，LIANG Bing-jie2，QIN Zhuo2
（1.Air Defence Institute，Air Force Engineering University，Xi’an 710051，China；2.Xi’an Branch，Datang Mobile Communications Equipment Limited Company，Xi’an 710061，China）

Non-subsample shearlet transform（NSST）is suggested into the multi-focus image fusion，for its advantage in image fusion and the feature of multi-focus imaging．Orientation information measurement can highlight the edge texture characteristic and reduce the noise，so it is used in the fusion of high-frequency coefficients．Therefore，the fusion image is brought out after the NSST inverse transformation is taken on the fusion of low-frequency and high-frequency coefficients．Simulation is carried out to prove the effectiveness and practicability the proposed technique，which illustrates that the proposed method can improve the quality of fusion images and increase the information of fusion images，meanwhile，the noise of images is also decreased．

image fusion；non-subsample shearlet transform（NSST）；orientation information measurement

TP 312

10．3969／j．issn．1001-506X．2015．01．31

邢雅琼（1986-），女，博士研究生，主要研究方向为智能信息处理。

E-mail：shmilyds520＠163．com

王晓丹（1966-），女，教授，博士，主要研究方向为智能信息处理、机器学习。

E-mail：afeu_w＠yahoo．com．cn

梁兵杰（1973-），男，高级工程师，硕士，主要研究方向为智能通信、信息安全。

E-mail：liangbingjie1＠datangmobile．cn

秦卓（1984-），男，工程师，硕士，主要研究方向为图像处理。

E-mail：qinzhuo＠datangmobile．cn

1001-506X（2015）01-0191-08