这道中考题得分为什么如此之低——由2015年安徽省数学中考第22题阅卷引发的思考

●刘国超 (阜阳师范学院附属中学 安徽阜阳 236041)



这道中考题得分为什么如此之低
——由2015年安徽省数学中考第22题阅卷引发的思考

●刘国超 (阜阳师范学院附属中学 安徽阜阳 236041)

笔者有幸参加了2015年安徽省阜阳市数学中考的阅卷工作，作为阅卷题组长，具体负责第22题的评判.结果统计表明，考生解答该题的情况很不理想，平均得分1.87分，得分率只有16%；其中得0分的占56.3%.面对如此多的零分情况，给了笔者极大的触动和思考，下面把阅卷过程中学生的一些典型错误以及笔者对错误的思考整理成文，以期广大同仁的交流、分享．

1 试题再现

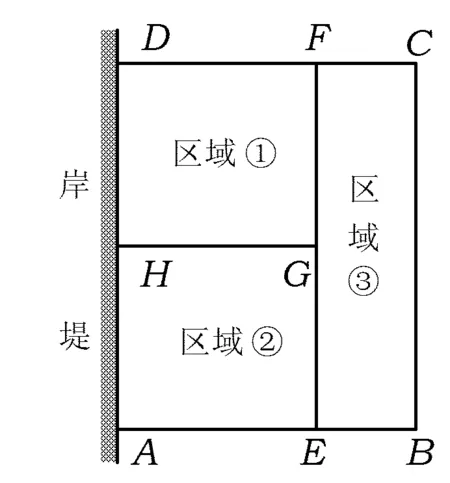
图1

题目 为了节省材料，某水产养殖户利用水库的岸堤(岸堤足够长)为一边，用总长为80 m的围网在水库中围成了如图1所示的①②③这3块矩形区域，而且这3块矩形区域的面积相等．设BC的长度为xm，矩形区域ABCD的面积为ym2．

1)求y与x之间的函数关系式，并注明自变量x的取值范围;

2)x为何值时，y有最大值,最大值是多少？

(2015年安徽省阜阳市数学中考试题第22题)

参考答案 1)设AE=a,BE=b，则

2x+3a+2b=80.

由2xb=ax,得a=2b,代入上式得

2x+8b=80,

即

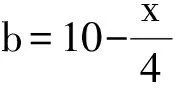
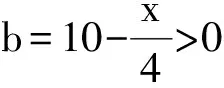
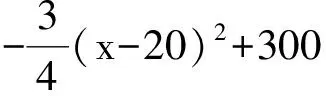
2)由第1)小题得，当x=20时，ymax=300.

考查目的 本题从考查的角度看是考查学生是否会根据实际问题列出二次函数解析式，并求面积最大值.情境设置看似平凡，但内涵丰富，颇具创意,主要针对“二次函数在实际生活中的应用”这个初中数学课程的重点内容.从思想的角度看本题涉及的数学思想主要有：一是数学建模的思想，主要体现在把实际问题抽象转化为方程模型、函数模型的过程；二是转化与化归思想，主要体现在第1)小题求函数解析式的过程中，即把数学问题中的“未知”逐步转化为“已知”的过程；三是数形结合思想，以实际问题为背景，融合几何直观，把数式计算和几何关系很好地结合起来．因此，这道中考题是一个很好的函数应用题，值得关注和重视．

试题以围成矩形区域的面积作为角度切入，源于教材，又高于教材．在课本题的基础上加以变化延伸，体现了“立足基础，渗透思想，突出能力，着重创新”的课改理念，具有较好的教学导向性.试题是由人教版《数学》九年级上册第57页习题第6题拓展而来：

课本习题 如图2，用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园，墙长为18 m，这个矩形的长、宽各为多少时？菜园的面积最大，最大面积是多少？

虽然试题与原型相比，让我们觉得“有本、有源”，由于在生活中用围网在水库中围成矩形区域没有用篱笆在平地上围成矩形区域更常见，因此从学生角度看，试题并没有散发出“就在身边的亲切感”．

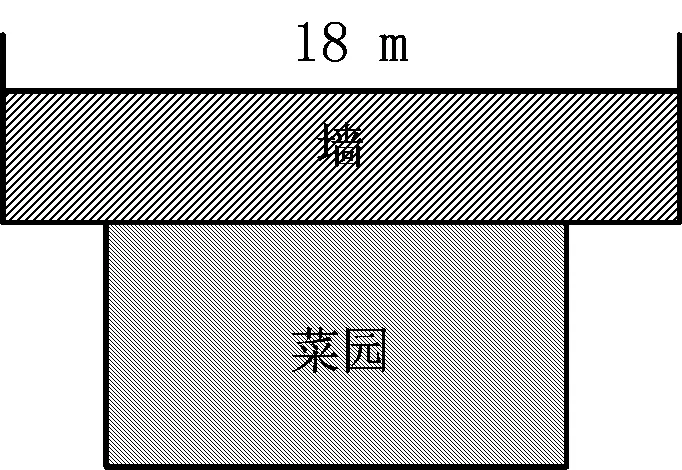
图2

为了体现数学的应用意识，命题者会设计一些现实情境，在现实情境中，除数学知识之外，还有其他因素.教师和学生的视角不同，教师关注的是现实情境中的数学,而学生更倾向于从现实生活的角度思考问题情境．题目情境给学生领会题意与分析问题带来很大的挑战，例如试题叙述的中间隔栏是不是用围网.学生一旦被这些所干扰，就会造成对理解问题的障碍，这是该题出现大量空白卷的原因之一，从而暴露试题在叙述上存在瑕疵！另一方面，二次函数应用问题的本质模型是根据二次函数求最值，试题通过3块矩形区域的面积相等作了“结构变式”，给学生“建模”设置了障碍，当然就不能顺利地“解模”，这也是造成该题得零分多的又一个原因．

2 学生的解答及相应的错误

通过阅卷发现学生的解答与命题者所期望的答案相差甚远．学生解答中的典型错误和主要原因有：

1)不敢设多元未知数．由于相当多的考生不能把“总长为80 m的围网在水库中围成了如图所示的①②③这3块矩形区域”和“而且这3块矩形区域的面积相等”这2个重要的已知条件，转换成方程模型，从而不能发现a，b及x之间的数量关系，这同时也表现出大部分学生受思维定势影响，没有大胆的“设元意识”，导致“不敢”再设其他辅助元，就没法建立函数关系式，多数考生在试卷上留下了一片片白色的遗憾.从另一个方面也反映出学生运用数学语言、用字母表示数的意识较弱，不知道使用字母表示数可以进行运算和推理.

2)化归能力薄弱．还有一部分考生也设辅助元了，这表明这部分学生有用字母表示数的意识，但在使用过程中，把问题中的条件符号化，以及怎样用恰当的数学式子表示问题的条件和结论出现了问题——学生不明确这里的运算对象“a，b”，没有把辅助元都向“x”靠拢，即用含“x”的代数式表示它们，导致思维受阻，从而不能正确得出函数解析式.这也说明学生把实际问题翻译成数学问题的能力欠缺.

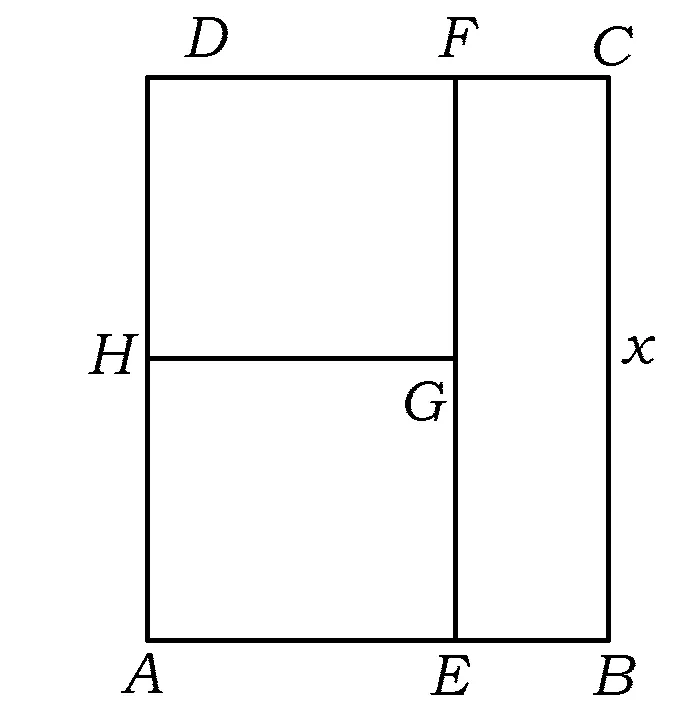
图3

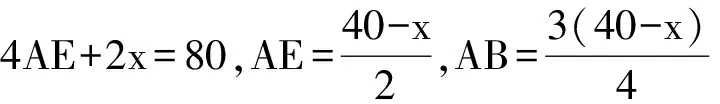
4)确定自变量取值范围存在问题．没有把含有自变量x的式子和图形中的线段对应起来，造成对自变量的取值范围判断错误，导致失分，这说明学生在解题习惯方面仍有不足.

6)该题的难点在于根据3个区域面积相等这一已知条件得出各边之间的关系，即FG=EG，DF=2CF,尤其是后者．但最根本的难点还是分析法思维，即要有如下的意识：在不知道各边关系的情况下，因为列出的函数关系式子中含有未知量CF和DF，要利用已知条件(面积相等、总长80、BC长为x)把它们表示出来的意识．还有相当一部分学生混淆了总长和周长，导致少算了HG，列错了函数关系式.

3 对课堂教学的启示

很多教师认为本题不难，但多数考生留下一片片白色的遗憾表明我们的日常教学存在失误和不足！大家知道，数学思想是形成数学思维的关键，通过学生对该题的解答可以看出，部分学生的数学思维还存在严重的缺陷，那么在实际教学中如何解决呢？

3.1 课堂教学要培养学生认真阅读题目的习惯

本题除了着重考查学生的理解能力、分析能力、数学建模能力之外，由于AE，AB与x的等量关系比较隐蔽，对学生的阅读理解能力的要求也比较高．很多学生不能顺利解答第1)小题的主要原因是没有认真阅读题目，不能分析出其中的已知量、未知量及它们之间的数量关系．给我们的教学启示：教学时呈现问题后，要留出时间让学生充分阅读题目，指导学生仔细读题、找问题关键词、确定它是什么样的数学问题，并引导学生尝试用自己的语言对已知量和未知量之间的数量关系进行描述；在对问题进行提炼、解决的过程中强调为什么要用字母表示数以及什么情况下用字母表示数，帮助学生对实际问题进行数学思考和数学理解，这才是突破数学模型建立的关键！

3.2 在课堂教学中，让学生经历模型建立的全过程

从实际情境中抽象出数学问题，这是数学建模的第一步，需要经历把实际情境到数学表达的思维过程，在这个过程中包含用数学符号建立方程、不等式、函数等来表达数学问题中的数量关系和变化规律，这是建立数学模型过程中极为重要的一个环节．在这个过程中既可以帮助学生建立数学模型，而且还可以提升学生的数学思维能力．可惜的是，笔者与一些教师交流后得知，平时的课堂教学中很少让学生经历思维活动的过程，大多都只是重视“解题类型和方法”，而忽视对过程的分析，以及对解题思维的培养.教师总是直接教“思维结果”，没有将“思维过程”教给学生，导致学生没有学习思维的方法，这样最直接的弊端就是学生缺乏独立思考、开拓创新的意识和能力，一旦碰到与实际生活相对疏远的问题就束手无策．

《义务教育数学课程标准(实验稿)》提出的“问题情境—建立模型—解释、应用于拓展”的研究学习模式，就是一个指导我们进行有效教学的策略.在实际教学时可以结合具体的数学内容采用这一模式，以学生为中心，以问题为主线，以培养能力为目标组织教学，让学生经历模型建立的全过程与知识应用的过程，从而更好地理解数学知识的意义，掌握必要的基础知识、基本技能，积累解决问题的经验，同时提高学生分析问题和解决问题的能力.实施这一策略的教学程序是：创设问题情境，激发求知欲；逐步概括，建立数学模型；分析模型，选用数学知识；问题解决，感受数学知识；归纳总结，升华数学知识．

3.3 课堂教学中关注建模思想的渗透

中考是短暂的,但是给我们留下的思考是长远的．在阅卷的过程中，笔者发现一部分学生仍然使用小学列算式的方法进行解答，这不得不引起教师的思考：经过3年的教学，学生对矩形边长关系的求解不会使用方程工具，其中的原因是什么？《义务教育数学课程标准(2011年版)》指出：学生学习数学的本质是思考，数学教学的重要目标就是培养学生的思考能力，学会数学地思考．因此在课堂教学中要重视对方程、不等式、函数等使用场合和使用方法的介绍，关注建模思想的渗透，这样学生对知识的理解就有了“源”，知识的运用就有了“根”，知识的拓展才会有“魂”！