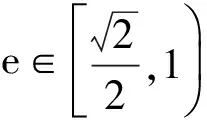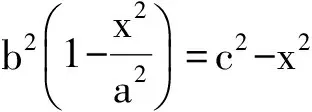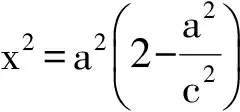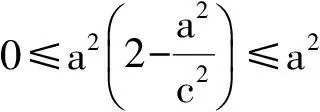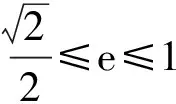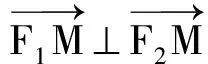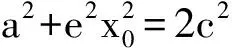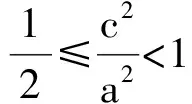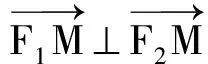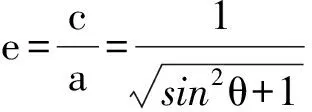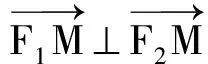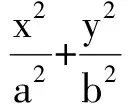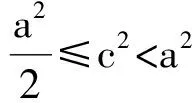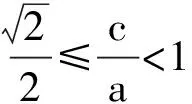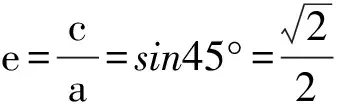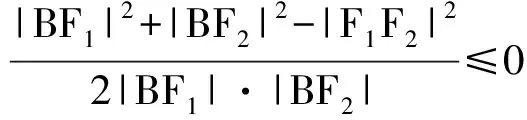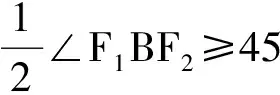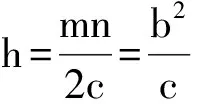一道求椭圆离心率范围题的多种解法

●李德安 (曲靖市第一中学 云南曲靖 655000)



一道求椭圆离心率范围题的多种解法

●李德安 (曲靖市第一中学 云南曲靖 655000)

研究椭圆离心率范围问题是圆锥曲线中的常见问题.下面通过几例常见题型，谈谈此类问题的一些常见解答.常见解答汇集成了一题多解，希望能给读者带来不常见的思维触动.

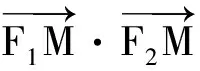
解法1 设点M的坐标为(x，y)，则

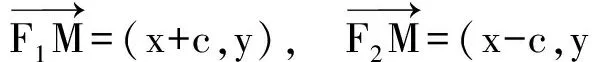
x2-c2+y2=0，

与椭圆方程b2x2+a2y2=a2b2联立得

c2x2+a2b2-a2c2=0.

该方程必有根，故

Δ=-4c2(a2b2-a2c2)≥0,

从而

b2≤c2,

于是

a2≤2c2,

即

故

又因为0

评注 联立方程、消元、“Δ”、韦达定理是解决解析几何问题的固用套路.解法1由等式到不等式的转化，是由于点M的存在性，其对应方程有解，从而得到Δ≥0，由这一不等关系求出e的范围.

点拨2 在代数变形过程中，注意借助椭圆中x,y的有界性求出e的范围.

解法2 在解法1中，可知

(1)

又点M在椭圆上，得

(2)

由式(1)和式(2)，得

即

因为0≤x2≤a2,所以

即

故

又因为0

评注 代数问题的解决，关键是变形，变形中洞察力要强，解答题目发展的方向源于变形中所带来的思维启发.

点拨3 利用椭圆的焦半径公式解题.

解法3 设M(x0,y0)，则

|MF1|=a+ex0, |MF2|=a-ex0.

从而

|MF1|2+|MF2|2=|F1F2|2,

即

亦即

由题意：点M在椭圆上，但不在x轴上，从而

于是

进而

0≤2c2-a2

即

故

评注 由垂直想到勾股定理，自然涉及到|MF1|,|MF2|的长度，通过焦半径公式，轻松找到含有x0,a,c,e的等式，再由x0的范围作为出发点，求出e的范围.

点拨4 通过三角代换(或参数方程)设出点M的坐标，将e用三角函数式表示.

又因为点O为F1F2的中点,所以

即

a2cos2θ+b2sin2θ=c2,

亦即

a2cos2θ+(a2-c2)sin2θ=c2，

从而

a2=c2(1+sin2θ)，

故

由θ∈(0,π)∪(π,2π),知0

故

即

评注 通过三角代换，借助正、余弦函数的有界性，求出e的范围，显得很自然.

b≤c

即

b2≤c2

从而

a2-c2≤c2-a2，

进而

于是

故

评注 问题化归到圆与椭圆必有公共点，通过数形结合，言简意赅，准确到位地找到不等式b≤c

点拨6 找到e取值的边界值，再分析取值范围b≤c

图1

解法6 如图1，当点M在短轴的顶点B(或A)处时，∠F1MF2取最大值.若∠F1BF2=90°，则

评注M是椭圆上的点，那么∠F1MF2的大小可以很小，甚至可以是0°.但∠F1MF2的最大值，并不是任意大的.因此，为了保证椭圆上存在点M使∠F1MF2=90°，应使∠F1MF2的最大值大于或等于90°，使∠F1MF2的最大值为∠F1BF2=90°，找到e的边界值再分析.解法6针对选择题、填空题显得更灵活.

点拨7 通过解法6，可知应使∠F1MF2的最大值∠F1BF2≥90°即可，为了保证∠F1BF2≥90°，可借助余弦定理.

解法7 由题意可知∠F1BF2≥90°，即

cos∠F1BF2≤0,

从而

即

2a2-4c2≤0，

进一步

故

评注 分析题目的本质，即∠F1MF2的最大值∠F1BF2≥90°，接下来从解三角形的角度，想到余弦定理.

点拨8 分析到∠F1MF2的最大值∠F1BF2≥90°，除了利用余弦定理，还可利用向量的数量积，去求e的范围.

解法8 由题意可知∠F1BF2≥90°，则

即

-c2+b2≤0，

亦即

a2-c2≤c2，

从而

评注 利用向量数量积的坐标表示，直接找到含b,c的不等式，从而求出e的范围.

解法9 由题意可知∠F1BF2≥90°，即

在Rt△OBF2中，

又因为0

评注 研究最大角的半角所满足的条件，来得更快.

点拨10 分别设出|MF1|,|MF2|的长度，再利用重要不等式，求出e的范围.

解法10 设|MF1|=m，|MF2|=n，则

(3)

(4)

由式(3)得m2+n2+2mn=4a2.

(5)

式(5)-式(4)，得

4a2-4c2=2mn≤m2+n2=4c2，

当且仅当m=n时，等号成立,即

2c2≥a2，

亦即

又因为0

评注 设|MF1|=m,|MF2|=n，由椭圆定义及题设条件可得到含有m,n及a,b,c的等式，通过代数运算，借助重要不等式，就找出了e的范围.虽引进了m,n这2个量，但整体结构的处理正是借助关于m,n的重要不等式得到所需不等式.

点拨11 在解法10的基础上，通过等面积法，由三角形高的范围求出e的范围.

解法11 由解法10可知

mn=2(a2-c2)=2b2.

设△F1MF2的边F1F2上的高为h，由等面积法可得

2ch=mn,

即

a2≤2c2,

得

又因为0

评注 从三角形高的范围，求出e的范围，可谓新颖.

解题的训练就是思维的训练，解题的过程就是化归转化的过程，使要解决的问题转化到我们熟知的范畴上；解题的过程就是解决矛盾的过程，矛盾在哪里，问题就在哪里，解题的突破口也就在那里；解题的过程就是联想的过程，联想可用怎样的方法原理解决这一新的问题；解题的过程更是创新超越的过程，要有勇气从不同的角度看问题，探究尝试一题多解，不易乐乎！

布鲁纳曾说过：“一个人学习一门学科的知识，不是要建立有关这门学科的小型图书馆，而是要掌握其知识结构和方法原理.只有这样，我们才能从知识的成品仓库进入知识的生产车间.”希望数学的解题能进入生产的车间.

本文是云南省曲靖市教育局、曲靖师范学院教育科学规划课题(项目编号：QJQSKT2015001)的研究成果之一.