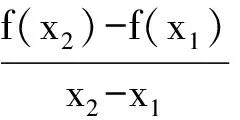解决型函数问题的常见错误及通用解法
2015-06-12林逸凡吉林大学附中实验学校吉林长春130000
●林逸凡 (吉林大学附中实验学校 吉林长春 130000)
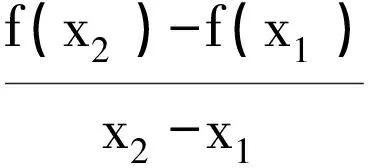
●林逸凡 (吉林大学附中实验学校 吉林长春 130000)
纵观近几年的高考试题,在数学高考与高等数学的衔接处命制题目已成为高考命题的特色之一,备受高考命题者的青睐.在这样的一个大背景下,学生们渐渐也对一些大学常用的数学工具不再陌生.例如,利用极限思想分析函数图像或数列的变化趋势,利用Jensen不等式解决复杂函数的不等式估计问题,利用洛必达法则求极限,利用隐函数求导求曲线的切线方程,利用二次求导研究函数凹凸性,等等.
掌握这些数学工具对于解决一些难题,特别是高考的压轴题是有帮助的.然而,由于认知的局限性,很多时候学生只是会机械地使用,知其然而不知其所以然,容易产生错误.以微分中值定理为例:
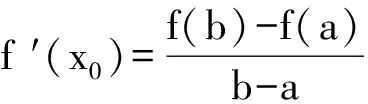
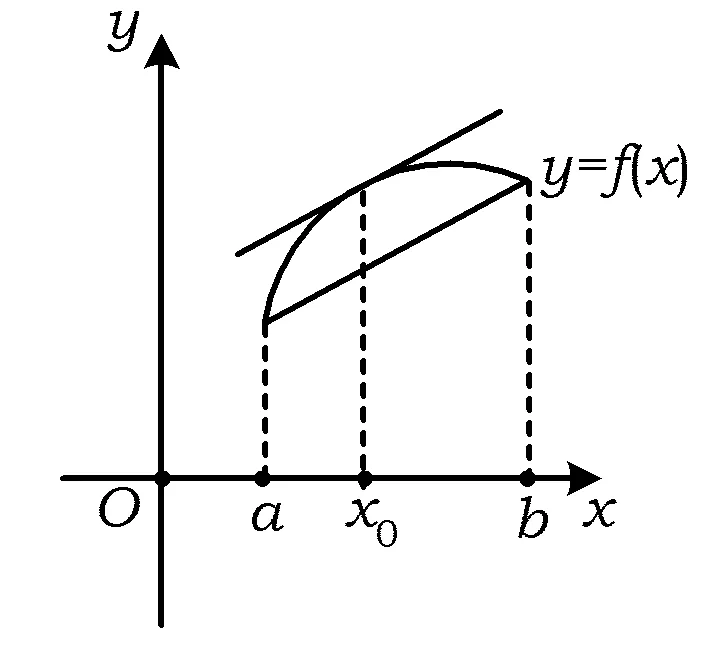
图1
如图1所示:其几何意义为在区间[a,b]上至少有一点x0的切线斜率与连接点A(a,f(a)),B(b,f(b))的线段的斜率相等.
微分中值定理对于学生来说较好理解,因为函数f(x)在区间[a,b]上连续可导,所以f(x)是连续并且(一阶)光滑的,在高中阶段还不能严谨地描述连续和(一阶)光滑的特性,但是完全可以直观感受.利用微分中值定理确实可以解决不少问题.
1 例题分析
例1 设n是正整数,r为正有理数.证明:

证明 设f(x)=xr+1(其中x≥1),根据微分中值定理得
f(n)-f(n-1)=f′(x0)(n-n+1),
其中x0∈(n-1,n),即

从而
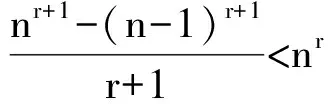
同理可证

如果利用微分中值定理不恰当,也会出现比较隐蔽的错误,以下面这个例题为例:
1)当a≤0时,讨论函数f(x)的单调性.
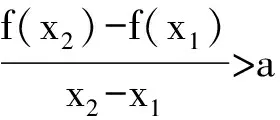
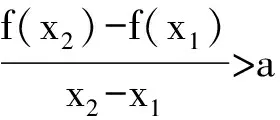
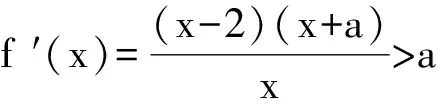
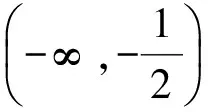
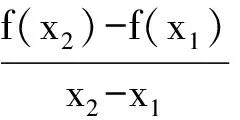
为了叙述方便,我们对函数f(x)作一个变换,令g(x)=f(x)-ax,则g′(x)=f′(x)-a,研究的问题等价于:条件“对任意的0
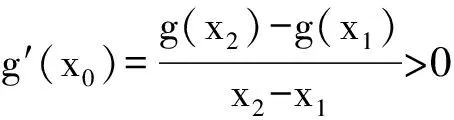

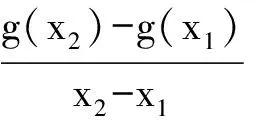
若“对任意x∈(a,b),g′(x)>0”,则“y=g(x)在(a,b)上单调递增”,需要注意2者并非是充要关系.即使假设g′(x)存在,反过来也是不对的:“y=g(x)在(a,b)上单调递增且g′(x)存在”,并不一定能够推出“对任意x∈(a,b),g′(x)>0”.
函数g(x)在区间上的增减性并不排斥在该区间存在点x0,使得g′(x0)=0.

图2


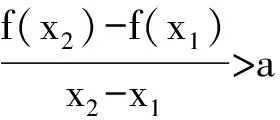
f(x2)-ax2>f(x1)-ax1.
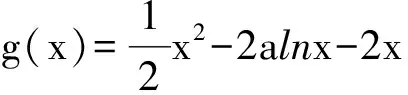
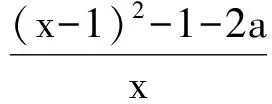
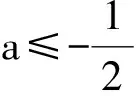
2 通法总结
-q(a)(x2-x1) (2014年陕西省数学高考文科试题第21题 第3)小题) 分析 令g(x)=f(x)-x,则 g′(x)=f′(x)-1, 对任意b>a>0, 变式2 设定义在区间(a,b)上的函数f(x),若任意x1,x2∈(a,b),x1≠x2,都有|f(x1)-f(x2)|<|x1-x2|,则称函数f(x)是区间(a,b)上的“平缓函数”. 1)求证:对任意k∈R,f(x)=x2+kx+14都不是区间(-1,1)上的“平缓函数”; 2)若f(x)是定义在R上的“平缓函数”,且f(x+2)=f(x)(其中x∈R),求证:对任意x1,x2∈R,x1≠x2,|f(x1)-f(x2)|<1. 分析 1)f(x)=x2+kx+14,假设f(x)是(-1,1)上的平缓函数,则对任意x1,x2∈(-1,1),x1≠x2,不妨设x1 |f(x1)-f(x2)|<|x1-x2| 等价于x1-x2 令g1(x)=f(x)+x,g2(x)=f(x)-x,则 g1(x1) 在(-1,1)上, 2)f(x+2)=f(x),f(x)是周期为2的周期函数,对任意x1,x2∈R,x1≠x2,f(x2)=f(x1+t),其中t∈(0,2).因为f(x)是R上的平缓函数,所以当t∈(0,1]时, |f(x1)-f(x2)|=|f(x1)-f(x1+t)|<|t|≤1; 当t∈(1,2)时, |f(x1)-f(x2)|= |f(x1+2)-f(x1+t)|< |2-t|<1. 综上所述,对任意x1,x2∈R,x1≠x2,|f(x1)-f(x2)|<1.
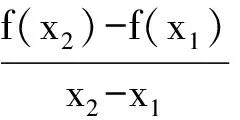
3 真题演练

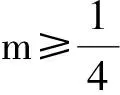
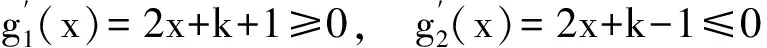
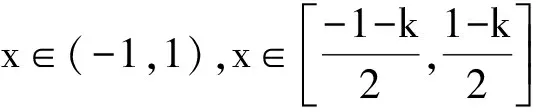


4 总结反思