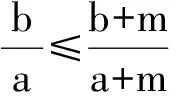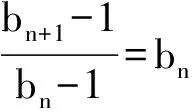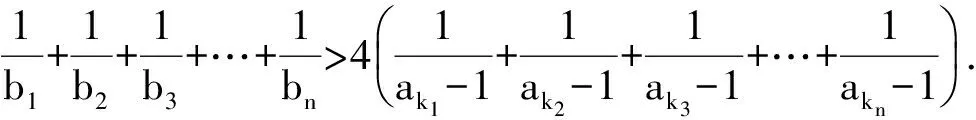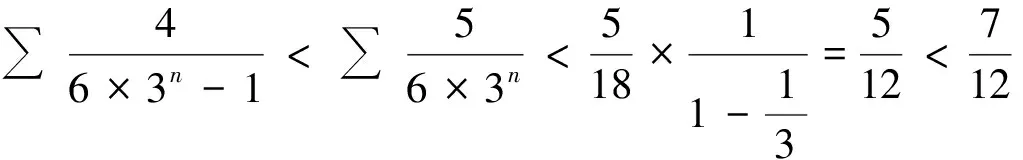一类数列不等式证明题的方法策略

●姚 杰 (湖州中学 浙江湖州 313000)



一类数列不等式证明题的方法策略

●姚 杰 (湖州中学 浙江湖州 313000)

证明数列型不等式，因其思维跨度大、构造性强，需要有较高的放缩技巧，从而充满思考性和挑战性，能全面综合地考查学生的潜能与后继学习能力，成为高考压轴题及各级各类竞赛试题命题的极好素材.这类问题中的典型代表即为证明“Sn<正常数”的题型，它的求解策略往往是：通过多角度观察所给数列通项的结构，深入剖析其特征，抓住其规律进行恰当地放缩.下面谈谈处理这类问题的3种策略.

策略1 能求和，先求和.

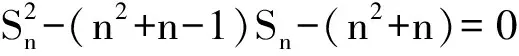
1)求数列{an}的通项公式an；

(2013年江西省数学高考理科试题)

分析 1)过程略，解得an=2n.

2)因为an=2n，所以

从而

下面着重阐述无法求和的此种证明题的方法策略.

策略2 先放缩再求和，一般要么放缩成裂项相消求和，要么放缩成等比数列求和，都可以用待定系数法.

例2 在正项数列{an},{bn}中，a1=2,b1=4，且an,bn,an+1成等差数列，bn,an+1,bn+1成等比数列.

1)求数列{an},{bn}的通项公式；

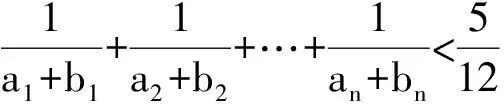
(2015年浙江省湖州中学模拟考试题)

分析 1)过程略，解得an=n(n+1)，bn=(n+1)2.

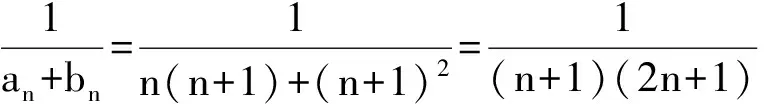
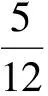
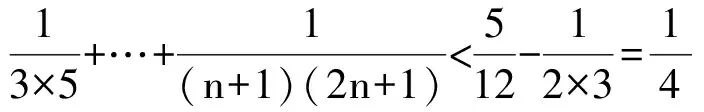
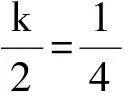
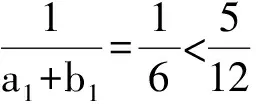
所以

反思 待定出来的系数一定要经得住检验；如果前几项不放缩的话,一定要注意n的范围变化；待定系数的过程可以在草稿纸上进行，书写出来的答案应该是想法成熟以后的结果.

例3 已知数列{an}的前n项和Sn满足2Sn=an+1-2n+1+1，且a1,a2+5,a3成等差数列.

1)求a1的值；

2)求数列{an}的通项公式；

分析 1),2)过程略.求得a1=1,an=3n-2n.

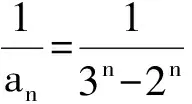
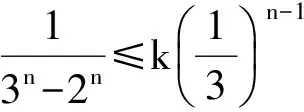
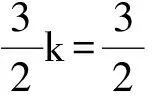
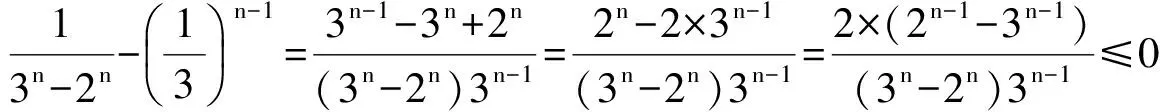
得

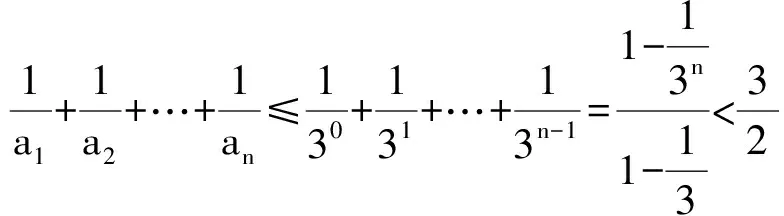
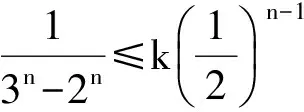
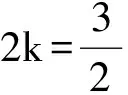
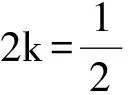
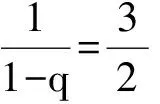
反思 放缩成等比数列的公比应该0

(2008年浙江省数学高考理科试题)

2)要证Sn>n-2，等价于证明∑(1-an)<2.左边根据条件中的递推式是可以用裂项相消法直接求和的，不需要放缩(证明过程略).

反思 若要证明的不等式2边含有n，则相对简单，因为任何含有n的式子f(n)，都能求出通项an=f(n)-f(n-1)(其中n≥2),所以只要比较通项的大小即可.麻烦的就是“常数”，因为通项求和以后通常不是一个常数，所以需要我们去寻找哪个通项求和以后去掉含有n的部分就是那个待证的常数，这是需要技巧的.这就是笔者为何只介绍证明“Sn<正常数”题型的方法策略的原因.

例5 数列{an}是公差不为0的等差数列，a5=6；数列{bn}满足：b1=3,bn+1=b1b2b3…bn+1.

2)当a3>1且a3∈N*时，a3，a5，ak1，ak2，…，akn，…为等比数列．

①求a3；

分析 1),2)①略.

(注：若遇到“Sn>正常数”的情形，其实不用求和，一般可利用通项an>0，Sn递增，只要Sn≥S1即可.)