一点引两弦斜率积为定值充要条件的探讨及应用

●石向阳 (南雅中学 湖南长沙 410129)



一点引两弦斜率积为定值充要条件的探讨及应用

●石向阳 (南雅中学 湖南长沙 410129)

在数学高考和数学竞赛中，常常会出现这类问题：曲线上一定点P引出2条动弦PQ,PR，这2条弦斜率的乘积(即kPQ·kPR)为定值，求动直线QR恒过定点或kQR恒为定值．笔者经过深入地思考和探索，得出一组非常漂亮、实用的性质，现简洁整理出来，以飨读者．

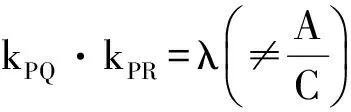
证明 作平移x′=x-x0，y′=y-y0，代入Ф(x，y)=0得

(1)

设QR的方程为lx′+my′=1，代入式(1)得

Ax′2+Bx′y′+Cy′2+(Φ1x′+Φ2y′)(lx′+my′)=0,整理得

(A+Φ1l)=0.

(2)

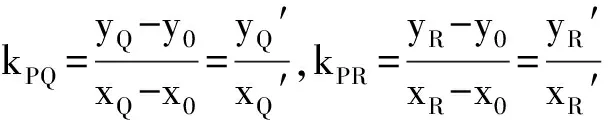
即

lΦ1+m(-λΦ2)=λC-A.

(3)

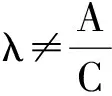
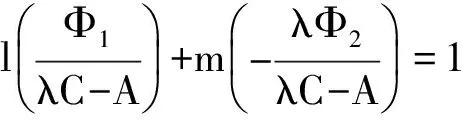
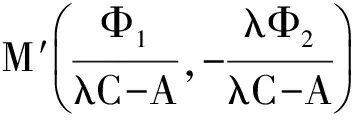
lΦ1+m(-λΦ2)=0,

即

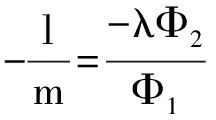
从而

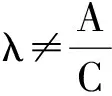
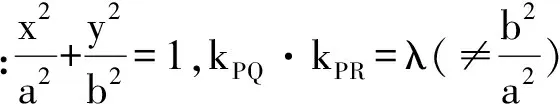
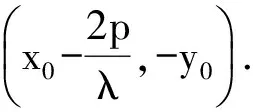
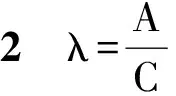
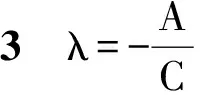
上述性质，不仅形式优美，而且能帮助我们迅速破解一些试题.

(2011年湖北省高中数学联赛预赛试题)

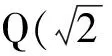
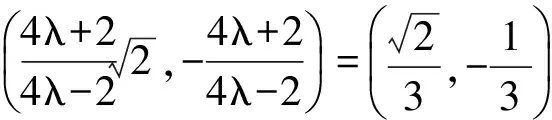
可得λ=-1，即∠AQB=90°．

例2 已知点A(1,2)，过点(5,-2)的直线与抛物线y2=4x交于另外2个点B,C，那么△ABC是

( )

A.锐角三角形 B.钝角三角形

C.直角三角形 D.不确定

(1999年全国高中数学联赛试题)

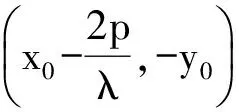
kAB·kAC=λ(≠0).

注意到当x0=1，y0=2时，令

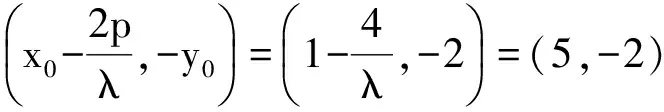
得

λ=-1，

图1

故选C．

例3 如图1，设点A和点B为抛物线y2=4px(其中p>0)上除原点以外的2个动点，已知OA⊥OB，OM⊥AB，求点M的轨迹方程，并说明它表示什么曲线？

(2000年安徽省春季数学高考试题)

解 因为OA⊥OB，所以

kOA·kOB=-1.

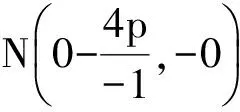
(x-2p)2+y2=4p2(其中x≠0).

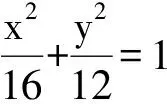
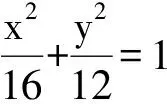
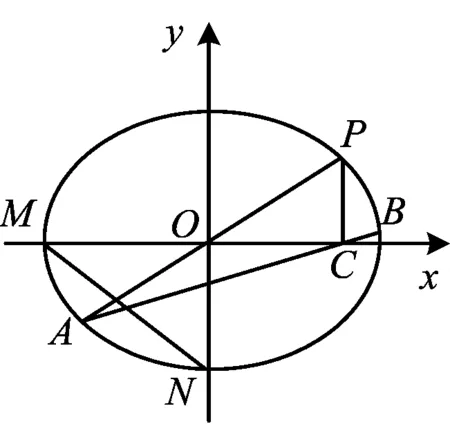
图2

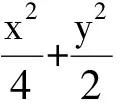
1),2)略；

3)对任意k>0，求证：PA⊥PB．

(2011年江苏省数学高考试题)

证明 设P(x0,y0)，则A(-x0,-y0)，C(x0,0)，由推论3知动直线AP过中心(0,0)的充要条件是

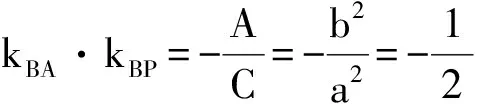
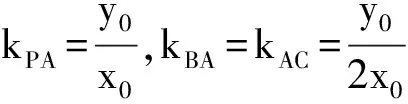
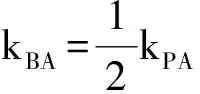
故

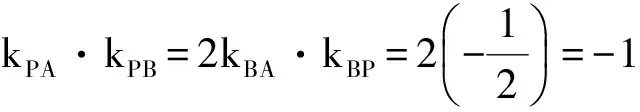
即

PA⊥PB．

例7 设A是单位圆x2+y2=1上的任意一点，l是过点A与x轴垂直的直线，D是直线l与x轴的交点，点M在直线l上，且满足|DM|=m|DA|(其中m>0,且m≠1)．当点A在圆上运动时，记点M的轨迹为曲线C．

1)求曲线C的方程，判断曲线C为何种圆锥曲线，并求其焦点坐标.

2)过原点且斜率为k的直线交曲线C于点P，Q，其中P在第一象限，它在y轴上的射影为点N，直线QN交曲线C于另一点H．问:是否存在m，使得对任意的k>0，都有PQ⊥PH？若存在，求m的值；若不存在，请说明理由．

(2012年湖北省数学高考理科试题)

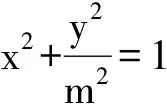
2)如图3，对任意x1∈(0.1)，设P(x1,y1)，H(x2,y2)，则Q(-x1,-y1)，N(0,y1).由推论3知动直线PQ过中心(0,0)的充要条件是

又点Q，N，H共线，从而

即

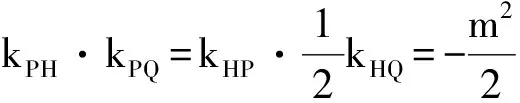
而PQ⊥PH等价于

kPH·kPQ=-1，

即

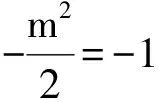
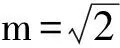
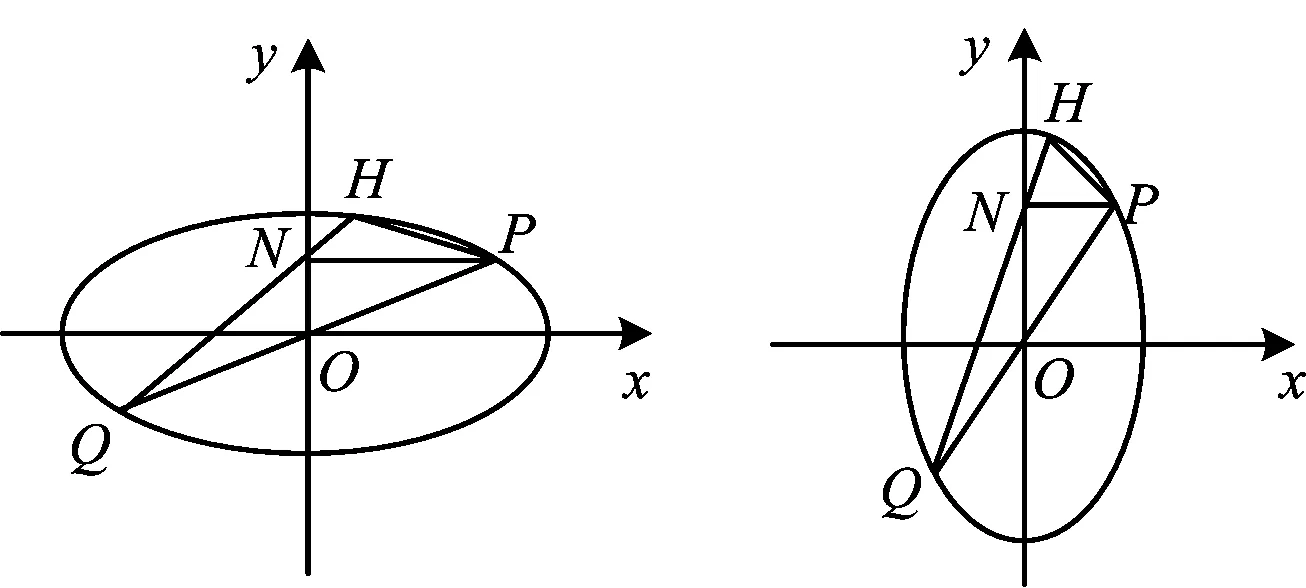
图3

例8 已知椭圆C:9x2+y2=m2(其中m>0),直线l不过原点O且不平行于坐标轴，l与C有2个交点A，B，线段AB的中点为M．证明：直线OM的斜率与l的斜率的乘积为定值.

(2015年全国数学高考新课标卷试题)

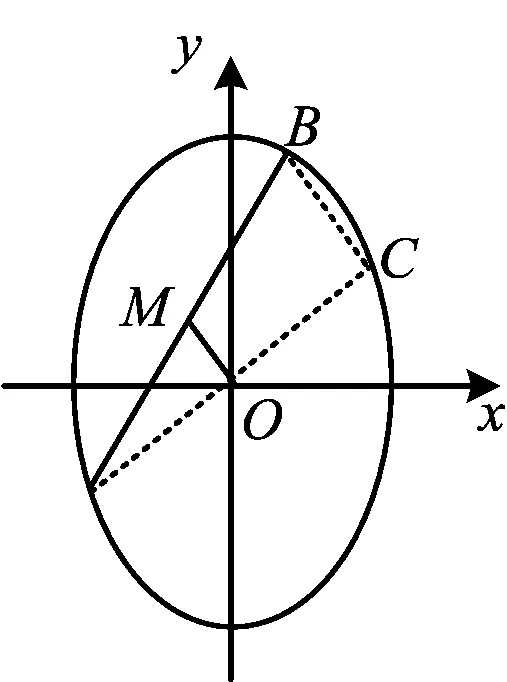
图4

证明 如图4，联结AO并延长与椭圆交于点C，联结BC，O为线段AC的中点，M为线段AB的中点，因此OM∥CB，即kOM=kCB．由推论3知动直线AC过中心(0,0)的充要条件是

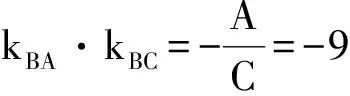
从而kAB·kOM=kAB·kCB=kBA·kBC=-9,

故直线OM的斜率与l的斜率的乘积为定值．