与角平分线性质有关的高考题探究

●周顺钿 (杭州高级中学 浙江杭州 310003)



与角平分线性质有关的高考题探究

●周顺钿 (杭州高级中学 浙江杭州 310003)

笔者在研究2015年全国各地的数学高考试题时，发现湖北省数学高考理科第14题和四川省数学高考理科第20题有着惊人的相似之处，在解决问题的过程中，又发现它们与三角形的角平分线有着紧密的联系，现整理如下：

1 角平分线的性质

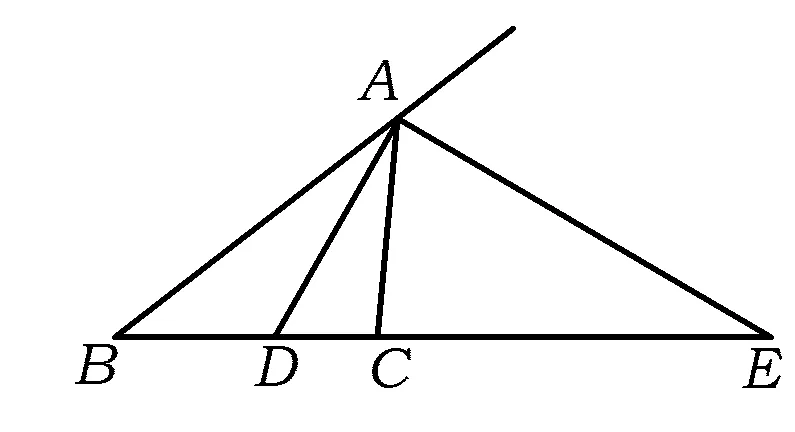
图1

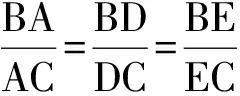
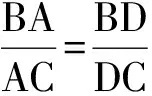
例1 如图2，⊙C与x轴相切于点T(1,0)，与y轴正半轴交于点A,B(点B在点A的上方)，且|AB|=2．

1)⊙C的标准方程为______.

2)过点A任作一条直线与⊙O:x2+y2=1相交于点M,N，下列3个结论：

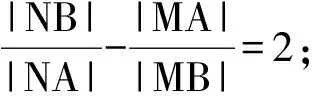
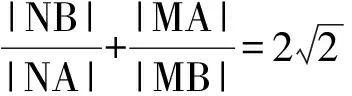
其中正确结论的序号是______(写出所有正确结论的序号).

(2015年湖北省数学高考理科试题第14题)

图2 图3

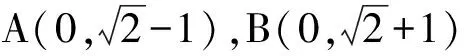
OT2=OA·OB.

因为ON=OT，所以

ON2=OA·OB，

故△OAN∽△ONB，从而∠ONA=∠OBN.同理可得，△OAM∽△OMB，得∠OMA=∠OBM.

又由OM=ON，得∠OMA=∠ONA，于是∠OBM=∠OBN，由内角平分线性质得

从而结论①成立.

因为

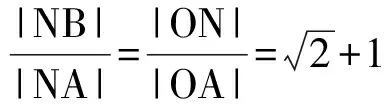
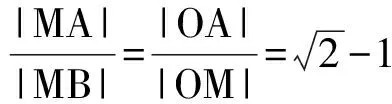
所以

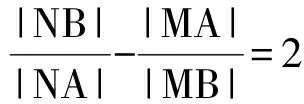
结论②③也成立.

评注 充分利用平面几何性质，可以快速高效地解决问题.

1)求椭圆E的方程.

(2015年四川省数学高考理科试题第20题)

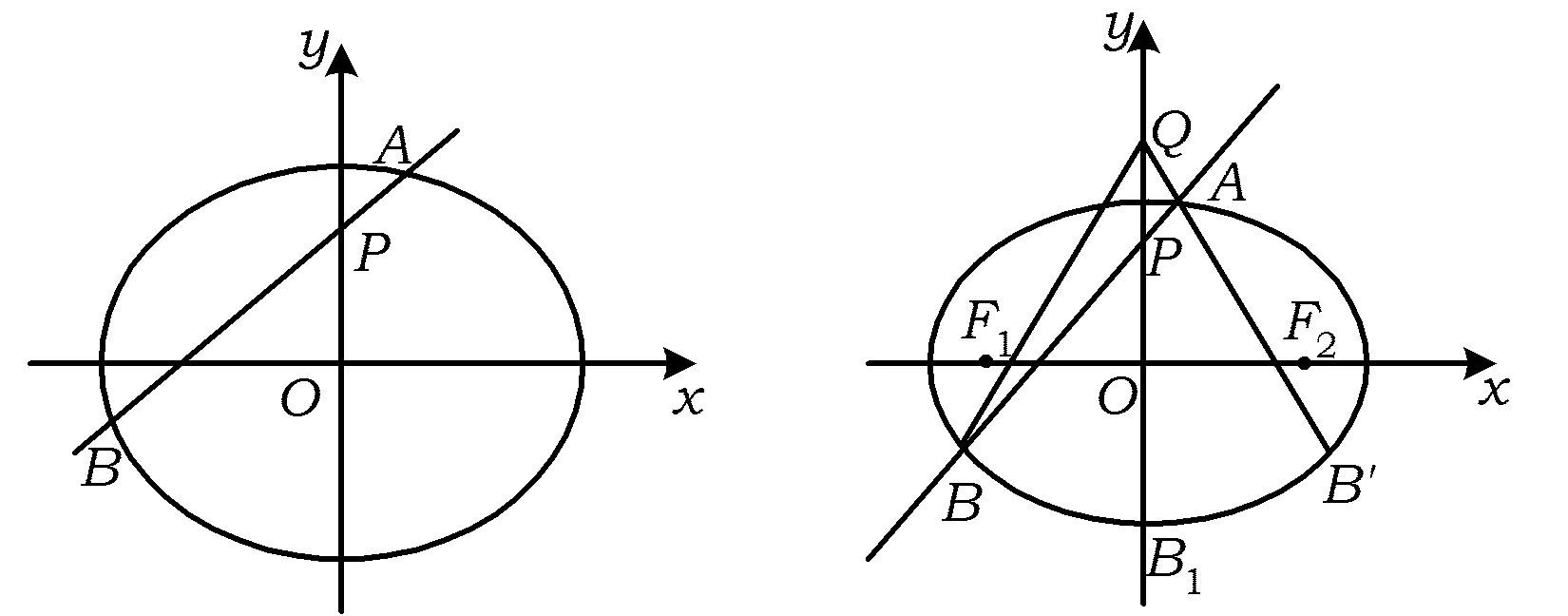
图4 图5

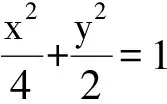
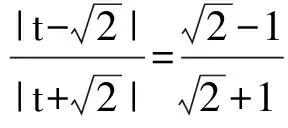
解得t=2，故点Q坐标只能为(0,2).

下证直线l的斜率存在且不为0时，结论也成立.

如图5,设l:y=kx+1，代入x2+2y2=4，得

(1+2k2)x2+4kx-2=0.

设A(x1,y1)，B(x2,y2),则

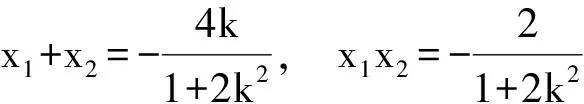
可得

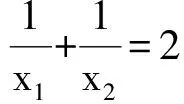
易知，点B关于y轴的对称点为B′(-x2,y2)，从而

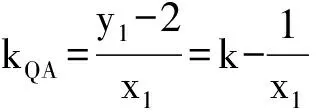
可得kQA=kQB′，即点Q,A,B′共线，因此

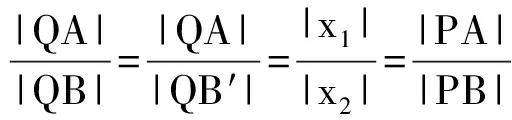
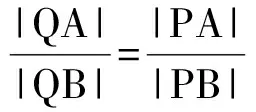
评注 特例探路，一般验证，是解决探究性问题的重要思想方法.

3 问题的探究

证明 设l:y=kx+r，代入b2x2+a2y2=a2b2，得

(b2+a2k2)x2+2kra2x+a2(r2-b2)=0.

设A(x1,y1)，B(x2,y2),则

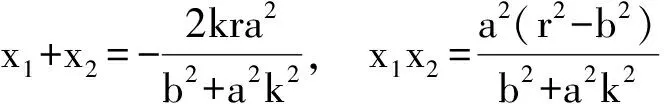
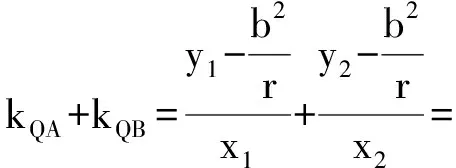
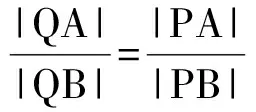
评注1 当0b时，点A,B在点P的同侧，PQ为∠AQB的外角平分线.

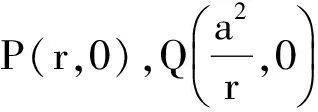
证明 设l:x=my+r，代入b2x2-a2y2=a2b2，得

(b2m2-a2)y2+2mrb2y+b2(r2-a2)=0.

设A(x1,y1)，B(x2,y2),则

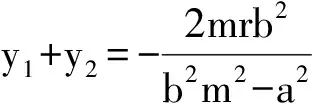
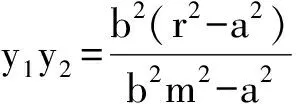
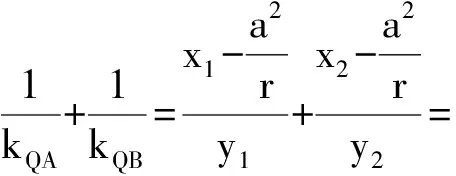
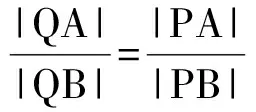
评注 对于双曲线，在实轴上存在满足条件的点对，在虚轴上不存在满足条件的点对.

4 问题的本质

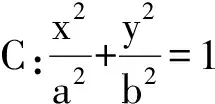
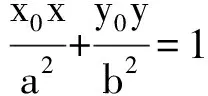
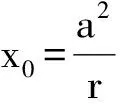
上述性质也可以推广到抛物线中去，请读者思考.