完全弹性支承变截面梁动力特性半解析解

闫维明， 石鲁宁， 何浩祥， 陈彦江

北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)



完全弹性支承变截面梁动力特性半解析解

闫维明， 石鲁宁， 何浩祥， 陈彦江

北京工业大学 工程抗震与结构诊治北京市重点实验室，北京 100124)

基于Bernoulli-Euler梁理论对直接模态摄动方法进行改进，建立求解完全弹性支承变截面梁振动方程的半解析方法。改进摄动法(IPM)在等效等截面完全弹性支承梁的模态空间内将变截面简支、连续梁的变系数微分方程组转化为非线性代数方程组，获得完全弹性支承变截面梁动力特性的半解析解；推导弹性边界条件下系数Δkki的具体计算公式。算例分析表明，改进摄动法计算精度高、收敛速度快，可有效考虑弹性支承对结构动力特性影响；据振型的对称性给出完全弹性支承变截面对称梁动力特性的简便计算方法(SIPM)；研究支座出现损伤对变截面简支梁桥自振频率影响。

改进摄动法；变截面梁；完全弹性支承；自振频率；振型

变截面梁广泛用于公路、城市桥梁中，其动力特性研究已成为热点；但变截面梁的振动方程均为复杂的高阶变系数微分方程，除个别结构能获得振动方程的解析解[1-2]外，大部分结构均无法获得精确解；而具有完全弹性支承的变截面梁的振动方程形式更复杂，常规方法无法获得解析解。完全弹性支承变截面梁广泛用于工程，如变截面简支梁桥、连续梁桥、轴承及阶梯梁等，因此需寻求适当方法获得完全弹性支承变截面梁振动方程的精确解。

Ece等[3]将变截面简支梁振动方程转化为空间坐标系下普通微分方程从而获得频率方程。Tong等[4]研究Timoshenko阶梯梁的动力特性并将变截面梁等效为多段等截面微梁段获得振动方程的近似解。Abrate[5]将变截面梁运动方程转化为等截面梁的运动方程获得变截面梁自振频率。钱波等[6]利用有限差分法研究变截面简支梁横向振动固有频率的数值计算方法；徐腾飞等[7]采用Frobeniu方法求解变截面Bernoulli-Euler梁的振动方程获得级数解。以上研究均未考虑弹性边界条件影响。Mao等[8-9]通过Adomian分解法研究变截面弹性支承Bernoulli-Euler梁的自由振动问题，但限于特定截面变化形式；Hosking等[10]研究带离散弹性支承等截面连续梁的振动问题，但不适用变截面梁。Lou等[11-13]给出的复杂梁动力特性近似分析方法-直接模态摄动法，考虑弹性支承均为跨内附加弹性支承，跨与跨间支承仍为理想铰支承，且计算均基于带铰支承的等截面梁模态摄动求解跨内带附加弹性支承与集中质量变截面梁模态。因此直接模态摄动方法无法用于求解具有完全弹性支承变截面梁(梁桥及轴承等结构形式)的振动方程。为此，本文针对该方法的不足进行改进，提出适用于求解完全弹性支承变截面梁动力特性的改进摄动方法(IPM)，并通过算例验证其有效性。据振型对称性对改进摄动方法进一步改进获得用于求解完全弹性支承变截面对称梁动力特性的简化计算方法(SIPM)；利用完全弹性支承变截面梁动力特性半解析解研究支座损伤对变截面简支梁动力特性影响。

1 完全弹性支承变截面梁振动方程

n跨完全弹性支承kb(b=1,2, …,n+1)变截面Bernoulli-Euler梁，见图1(a)，其自由振动方程为

(1)

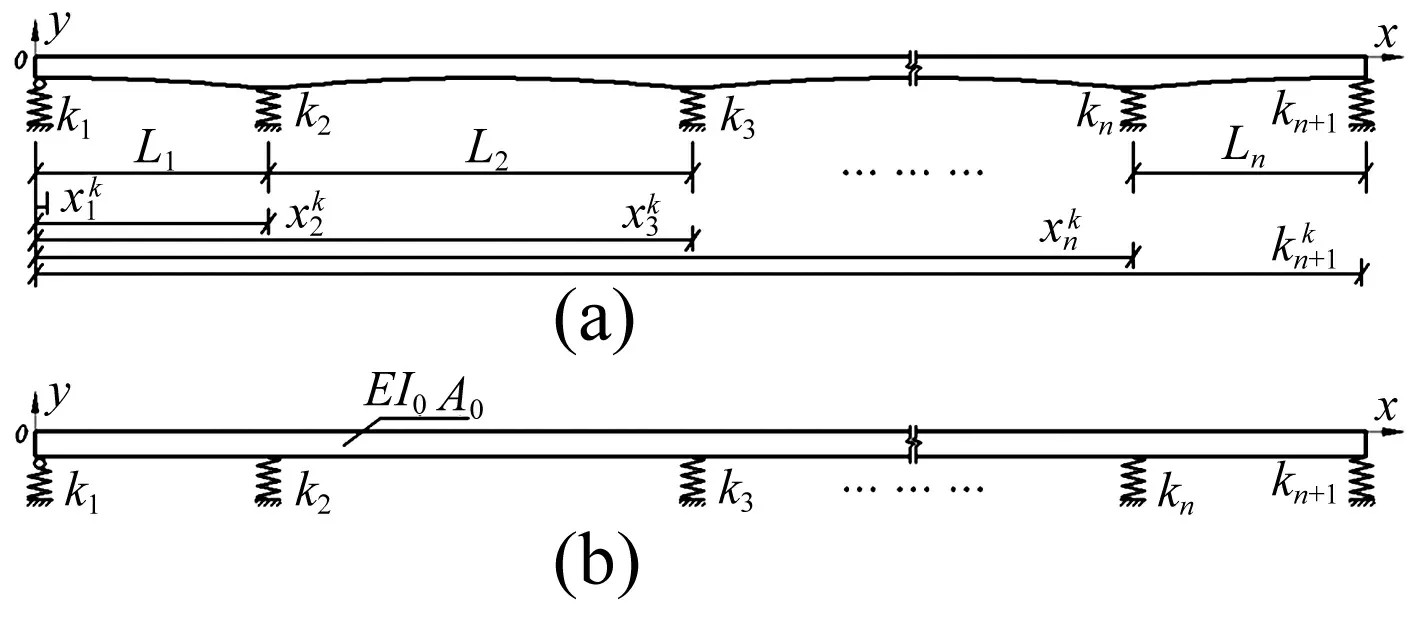
图1 完全弹性支承变截面梁计算模型Fig.1 Computa tion model ofnon-uniform beam with complete elastic supports

用变量分离方法[14]求解式(1)，设解的形式为

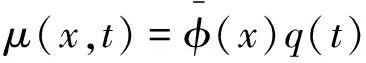
(2)

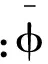
将式(2)代入式(1)，整理得

(3)

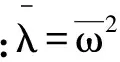
式(3)为高阶变系数微分方程，本文利用改进摄动方法求解完全弹性支承变截面梁的振动问题，获得求解式(3)精确高效的解析方法。

2 改进摄动法

直接模态摄动法均以带铰支承等效梁的模态解析解摄动求解变截面梁的振动方程。该方法可考虑跨内带附加弹性支承影响，但无法考虑弹性支座影响，因此直接模态摄动方法不适用求解完全弹性支承变截面梁振动问题。本文提出以完全弹性支承等效梁模态解析解摄动求解式(3)方法，改进的摄动方法(IPM)可有效求解完全弹性支承变截面梁振动问题。

2.1 改进模态摄动法公式推导

取与完全弹性支承变截面梁相同跨径布置及材料特性的弹性支承等效等截面Bernoulli-Euler梁(图1(b))，等效梁截面参数计算式为

(4)

(5)

式中：I0为梁截面惯性矩；A0为梁截面面积；L为梁长。

变截面梁惯性矩I(x)与面积A(x)关系为

ΔI(x)=I(x)-I0

(6)

ΔA(x)=A(x)-A0

(7)

式中：ΔI(x)，ΔA(x)为x处变截面梁相对等效梁截面惯性矩及面积变化量。

完全弹性支承等效梁(图1(b))自由振动方程为

(8)

直接模态摄动法带铰支承等效梁的振动方程为式(8)去掉第三项后的形式，显然两种方法存在明显差异。设等效梁第i阶振动主模态函数为φi(x)，则等效梁的特征方程可表示为

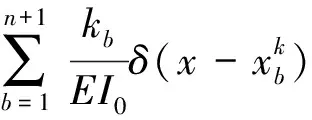
(9)

式中：λi为等效梁第i阶特征值。

将式(3)的完全弹性支承变截面梁视为图1(b)完全弹性支承等效等截面梁经截面惯性矩I0及面积A0变化后所得新体系，其主模态函数及特征值设为

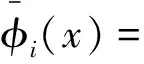
(10)

(11)

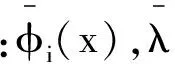
除φi(x)外等效梁其它保留主模态函数线性组合为

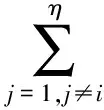
(12)

式中：qj为模态线性组合系数。

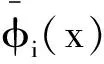
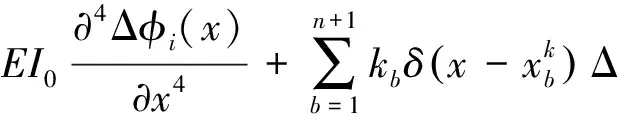
λiρA0Δφi(x)-λiρΔA(x)φi(x)-λiρΔA(x)Δφi(x)-

ΔλiρA0φi(x)-ΔλiρA0Δφi(x)-ΔλiρΔA(x)φi(x)-

ΔλiρΔA(x)Δφi(x)=0

(13)

将式(12)代入式(13)，两边同乘φk(x)(k=1,2, …,η)，沿梁长L积分，并利用完全弹性支承等效等截面Bernoulli-Euler梁模态正交性简化为

Δkki-λiΔmki

(14)

式中：

(15)

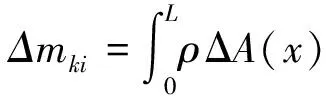
(16)

(17)

式(15)、(16)可直接采用数值积分获得，但式(17)需先简化。为此，本文将推导式(17)的简化公式。分别令式(14)中k=1,2, …,η，获得η个关于未知数Δλi及qj的非线性代数方程，整理简化为矩阵形式为

[A-B+λiC+λiDqi]q-p=0

(18)

式中：

式中：q为位置向量，其第i个元素qi=Δλi/λi。

由此将变系数微分方程式(1)转化为非线性矩阵方程式(18)。

2.2 弹性边界条件系数计算

直接利用式(17)较难获得系数Δkki值，需将式(17)化简间接获得该值。已有文献未给出具体计算方法，本文利用振型正交性及弹性边界条件推导该系数计算公式。将式(6)代入式(17)整理得

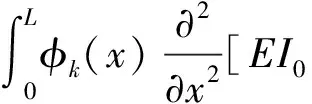
(19)

将式(9)代入式(19)，据振型正交性简化得

(20)

将式(20)第一项两次分部积分得

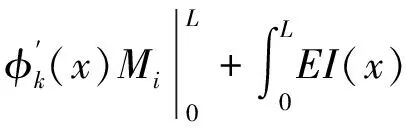
(21)

上式第一项为第i阶振型边界剪力在第k阶振型位移所做功，第二项为第i阶振型边界弯矩在第k阶振型转角上做的功。对图1(b)弹性支承等效梁而言，式(21)第二项恒为零，整理得

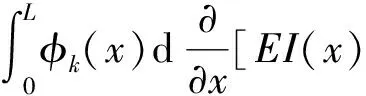
(22)

利用弹性支承等效梁边界条件化简式(22)代入式(20)并整理得

k1φk(0)φi(0)+kn+1φk(L)φi(L)

(23)

由此知，利用式(23)可方便求得系数Δkki值。

2.3 非线性矩阵方程组求解

对非线性矩阵方程组式(18)的求解可用牛顿-拉夫逊法或遗传算法、粒子群算法及模拟退火算法等并行智能算法；鉴于式(18)的Jacobian矩阵各项均为一次函数形式，较易获得，因此本文采用牛顿-拉夫逊法[15]求解。牛顿-拉夫逊法对初值选取非常重要，给定合理初值不仅可减少迭代次数且可获得更准确结果。据式(18)物理意义及向量q内各组合系数含义给定初值为

q=0

(24)

迭代终止条件为

(25)

式中：上角标κ为求解第i阶Δλi/λi系数时方程迭代次数；ξ为收敛误差。

将所得未知向量q代入式(10)、(11)，可求得完全弹性支承变截面梁第i阶自振频率及振型。令式(10)、(11)中i=1,2,…,n，重复上述迭代过程可获得完全弹性支承变截面梁前n阶模态参数。

2.4 完全弹性支承等截面梁特征方程的解析解

为利用完全弹性支承等截面梁的模态摄动求解完全弹性支承变截面梁模态参数，需获得该等截面梁特征方程的解析解。其第i跨模态函数表达式[16-17]为

(26)

式中：a4=mω2/EI，ω为圆频率；ai，Bi，Ci，Di为实常数。

据各支弹性支承处变形协调关系得

支承1处

(27)

支承n+1处

(28)

中间支承2～n处

(29)

将式(26)代入式(29)整理得

(30)

式中：

Hi-1=

循环利用式(30)可得

(31)

将式(26)代入式(27)、(28)得

(32)

(33)

式中：

将式(32)、(33)代入式(31)可得n跨完全弹性支承梁的频率方程为

det(ΦUnNn-1Un-1Nn-2…U2N1Ψ)=0

(34)

通过式(34)可获得n跨完全弹性支承的自振频率，将其代入式(31)反复利用式(30)可依次获得实常数Ai，Bi，Ci，Di值，并代入式(26)可获得n跨完全弹性支承梁的振型函数。

3 改进摄动法(IPM)算例验证

3.1 简支梁

完全弹性支承变截面简支梁见图2，长L=10 m，宽0.5 m，壁厚0.1 m，梁高按线性变化；弹性支承刚度k1=k2=1×105kN/m，材料弹性模量约1.6×1010N/m2，密度约3 000 kg/m3；等效梁惯性矩I0=0.004 m4，面积A0= 0.12 m2，收敛误差ξ=1×10-8。改进摄动方法、文献[9]方法及有限元法(单元长度0.1 m)计算所得前5阶频率见表1。改进模态摄动方法(η=9)及其它方法所得前5阶振型见图3。

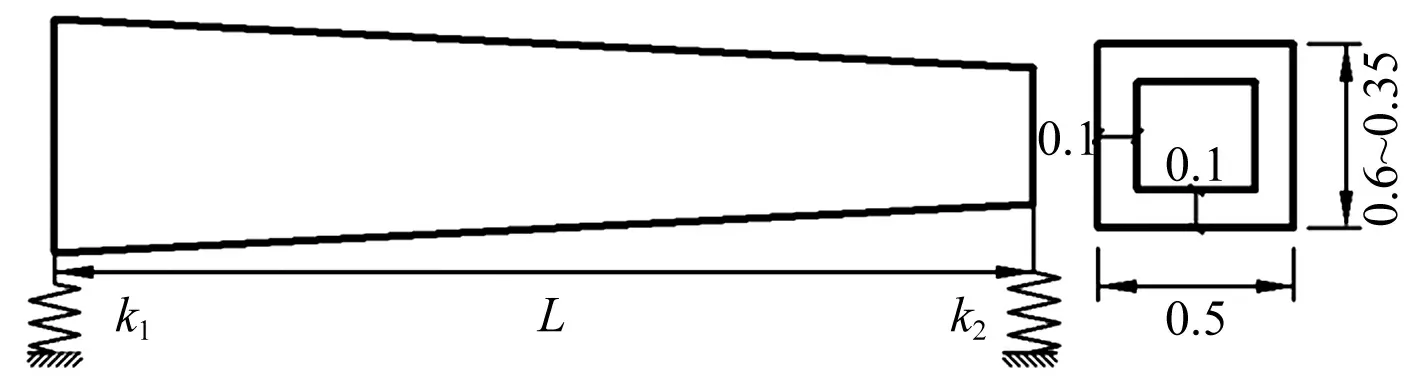
图2 变截面简支梁(单位m)Fig.2 Non-uniform simply supported beam

图3 简支梁振型图Fig.3 Mode shapes of simply supported beam

表1 简支梁自振频率(单位：Hz)

Tab.1 Freq uencies of simply supported beam (Unit: Hz)

计算方法模态阶次12345文献[9]方法5．5931421．6513045．3752672．43695102．09113有限元方法5．5935521．6564345．3864872．47292102．18170本文方法(η=13)5．63687(3)21．83593(4)45．78902(4)73．12983(5)103．12689(5)本文方法(η=11)5．63859(3)21．84191(4)45．79165(4)73．19531(5)103．19657(5)本文方法(η=9)5．63929(3)21．84771(4)45．80685(4)73．21592(5)103．21625(5)本文方法(η=7)5．64105(3)21．85126(4)45．81213(4)73．30269(5)103．35562(5)有限元法(铰)5．6599622．7339451．0707790．71991141．68780本文方法(η=13，铰)5．66238(3)22．72979(4)51．05181(4)90．68339(4)141．71094(5)

注：括号内数值为计算迭代次数；“铰”表示边界条件为理想铰支承。

3.2 两跨阶梯梁

完全弹性支承两跨阶梯梁见图4，跨径L1=L2=5 m，梁高0.3 m，左跨梁宽0.5 m，右跨梁宽0.3 m，弹性支承刚度k1=k2=k3=2.0×107kN/m，材料弹性模量210 GPa，密度7 850 kg/m3，等效梁惯性矩I0=0.1 m4，面积A0= 0.000 85 m2，收敛误差ξ=1×10-8。改进摄动方法、文献[8]方法及有限元法(单元长度0.1 m)计算所得前5阶频率见表2。改进模态摄动方法(η=9)与其它方法所得阶梯梁前5阶振型见图5。

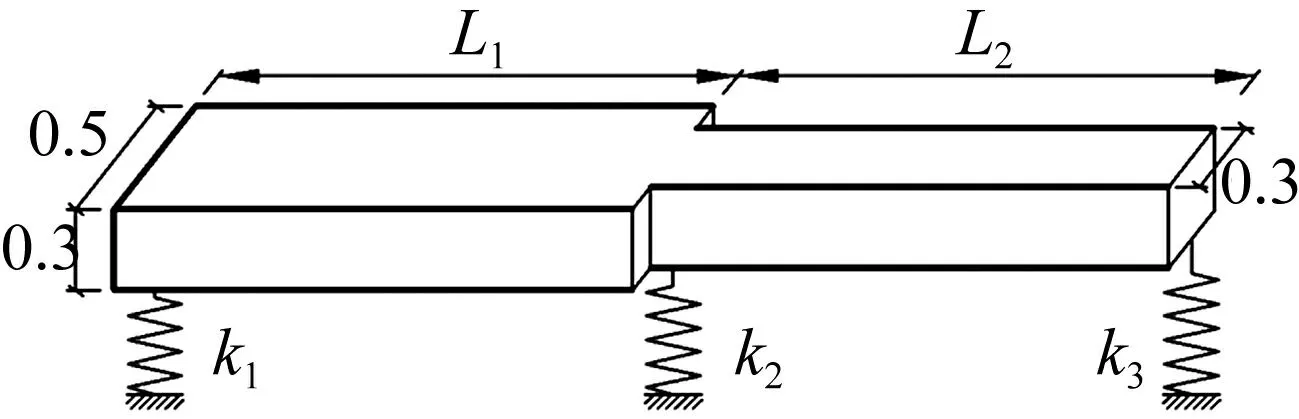
图4 两跨阶梯梁(单位m)Fig.4 Two-span stepped beam

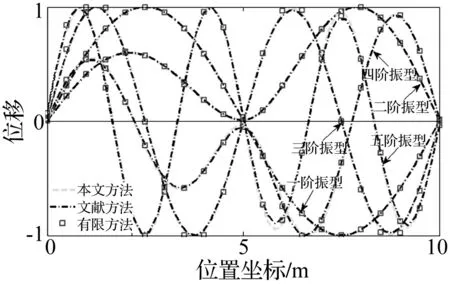
图5 两跨阶梯梁振型图Fig.5 Mode shapes of two-span stepped beam

表2 两跨阶梯梁自振频率(单位：Hz)

Tab.2 Freg uencies of two-span stepped beam (unit: Hz)

计算方法模态阶次12345文献[8]方法26．7521741．60236106．78979133．18575239．42214有限元方法26．7487941．61601106．73371133．33598239．09972本文方法(η=13)26．76925(3)41．89489(4)107．06126(3)135．25317(4)240．94012(4)本文方法(η=11)26．76980(3)41．89729(4)107．06880(3)135．26780(4)241．13879(4)本文方法(η=9)26．77208(3)41．95417(4)107．10473(4)135．35991(4)241．11264(4)本文方法(η=7)26．77258(3)41．99813(4)107．11060(4)135．77552(4)241．20464(4)

注：号内数值为计算迭代次数。

由表1、表2看出，本文IPM法计算所得前5阶自振频率与文献[8-9]及有限元结果均吻合较好，且IPM法所得各阶自振频率随η取值增大而趋向更精确结果。η=7～13时IPM法计算结果略大于文献[8-9]及有限元计算结果，但IPM计算结果(η=13)与文献[8-9]理论计算结果及有限元数值计算结果误差均在1.5%内，工程上可接受。本文忽略高阶模态参数对摄动结果影响，而误差为取η值7～13所致截断误差，故略大于有限元数值结果；算例中有限单元长度均为0.1 m，网格划分较细，计算结果更接近解析解；本文计算结果精度不及有限元。IPM法属于Ritz法，计算结果高于结构真实值，理论上η取值越大结果越接近真实值。由图3、图5看出，IPM法所得弹性支承变截面梁前5阶振型与文献及有限元结果较一致；对比不同方法各阶振型弹性支承处位移及表1第9，10行数据可知，IPM法能有效考虑弹性支承对结构动力特性影响，能获得具有足够精度、完全弹性支承变截面梁模态参数。

本文IPM法仅需知道完全弹性支承变截面梁材料、截面、跨径及支座刚度信息即可获得结构模态参数。而有限元方法不仅需上述信息且需几何建模及网格划分，计算精度与网格质量、尺寸有关，计算效率与节点、单元数量有关，因此IPM法在计算速度、精度上具有有限元方法无法比拟的优势；有限方法进行参数敏感性分析时需手动调节参数值，计算工作量大。而IPM法获得完全弹性支承变截面梁的半解析解可方便快速进行参数敏感性分析，其优势显而易见。

4 改进摄动法在对称梁中简化计算方法

4.1 简化计算原则及公式

据跨径、截面对称布置的完全弹性支持变截面梁振型对称性将式(18)进行简化。据动力学基本理论，完全弹性支承变截面对称梁奇、偶数阶振型对称性相同，而奇数阶振型对称性总与偶数阶振型对称性相反。

据式(12)在摄动求变截面梁的偶数阶振型时，等效梁的奇数阶振型对称性与偶数阶振型对称性相反将对式(18)求解起干扰影响，会增加迭代次数，影响收敛速度。因此，在摄动求解偶数阶模态参数时可仅利用等效梁的偶数阶振型忽略奇数阶振型影响；因此，利用等效梁前η阶(设η为偶数)振型摄动求解时，式(18)可简化为

[Ac-Bc+λiCc+λiDcqci]qc-pc=0

(34)

式中：i=2, 4, 6,…；

由此，将式(18)的η个非线性方程组求解简化为式(34)的η/2个非线性矩阵方程式(28)的求解。摄动求解奇数阶模态参数时可仅利用等效梁的奇数阶振型。利用等效梁的前η阶(设η为奇数)振型摄动求解时，式(18)同样可简化为式(34)形式，但各参数需相应变化，取i=1, 3, 5,…；将式(18)η个非线性方程组的求解简化为式(34)的(η+1)/2个非线性矩阵方程式(33)求解。

4.2 简化计算方法验证

完全弹性支承变截面简支梁桥见图6，分别利用IPM法、SIPM法摄动求解模态参数见表3、表4 (限于篇幅仅给出前两阶频率对比结果)。桥梁跨径为20 m，混凝土标号C50，梁底下缘及底板上缘均按二次抛物线变化，支座实际刚度为7.6×105kN/m，计算收敛误差ξ=1×10-8。改进摄动方法及简化方法计算所得前5阶振型见图7 (η=9)。

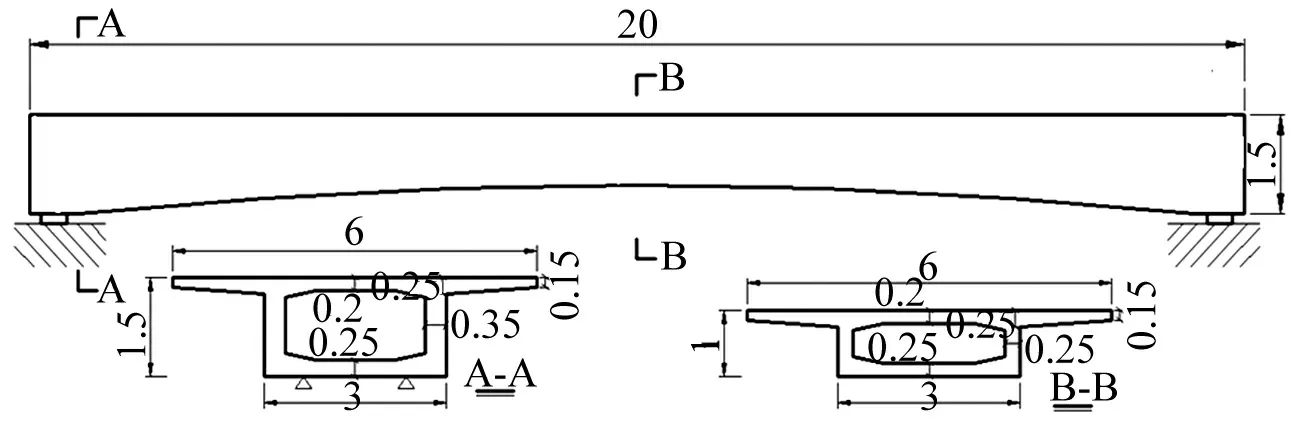
图6 简支梁布置图 (单位: m)Fig.6 Genera l l ayout of simply supported beam

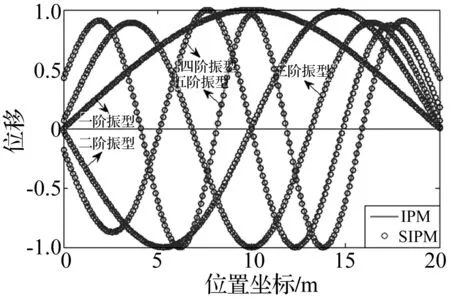
图7 简支梁振型图Fig.7 Mode shapes of simply supported beam

表3 一阶频率摄动结果

Tab.3 The perturb ation results of first order frequency

注：IPM为改进摄动方法；SIPM为对称变截面梁改进摄动法的简化计算法。

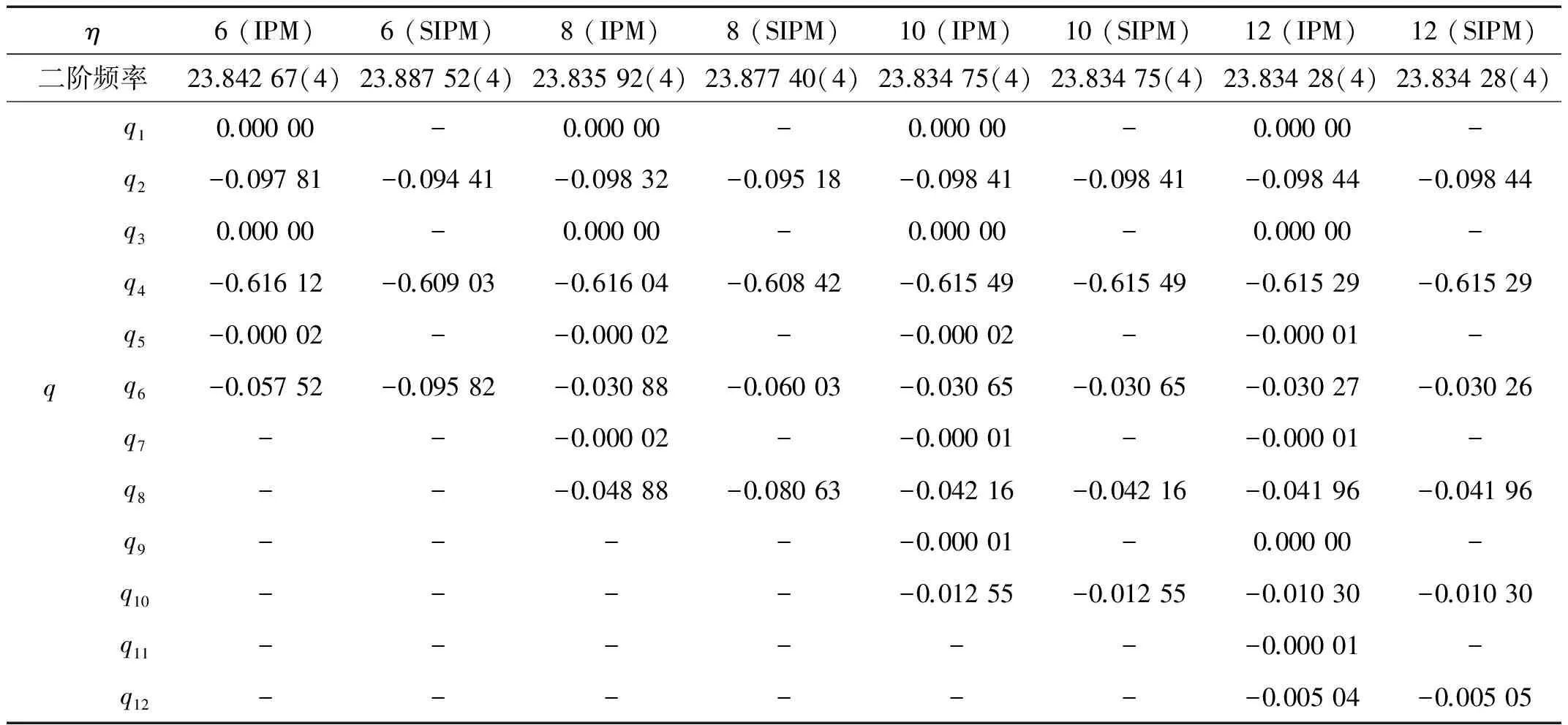
表4 二阶频率摄动结果

由表3、表4可知，用SIPM法求解变截面对称简支梁桥的第一、二阶频率与IPM法计算结果十分接近，计算迭代次数无明显增加。取相同η值分别用IPM法、SIPM法摄动求解奇数阶模态，IPM法所得q2,q4,… ,q2n值均接近于零，而所得q1,q3,… ,q2n+1值与SIPM法对应的组合系数值较接近；摄动求解偶数阶模态时亦有此规律，说明在摄动求解对称梁奇数阶模态时可忽略偶数阶模态影响，仅用等效梁的奇数阶模态求解；反之亦然。对完全弹性支承变截面对称梁用SIPM法求解模态参数，计算精度与IPM法接近。SIPM法系数及未知数数量均较IPM法减少约50%，显然SIPM法效率更高。

5 支座损伤对变截面简支梁桥动力特性影响

长期荷载、环境因素作用下的桥梁支座会出现不同程度损伤，在偶然荷载下甚至会出现支座失效，均会导致支座刚度不同程度下降。本文以完全弹性支承变截面简支梁为例，用IMP法分析支座刚度下降(0～30%)对结构前六阶自振频率影响，见图8、图9。由两图看出，支座出现损伤后随刚度下降各阶自振频率下降较明显；随支座损伤程度增大各阶自振频率变化率增加；支座出现损伤初期，对自振频率影响较少。单个支座出现30%损伤时，结构基频下降约0.8%，第六阶频率变化最小，约0.5%；而第三阶频率变化最大，约下降6.2%。两支座出现不同程度损伤时，各阶自振频率均随其损伤程度增加而降低；两支座均出现30%损伤时基频下降约1.5%。第六阶频率变化最小，约1.0%；而第三阶频率变化最大，约下降11.7%。各阶自振频率对支座损伤敏感性各异，并呈现明显的非线性关系。因此，通过寻找频率对支座损伤较敏感阶次用本文的半解析解可对支座刚度、损伤进行识别研究。

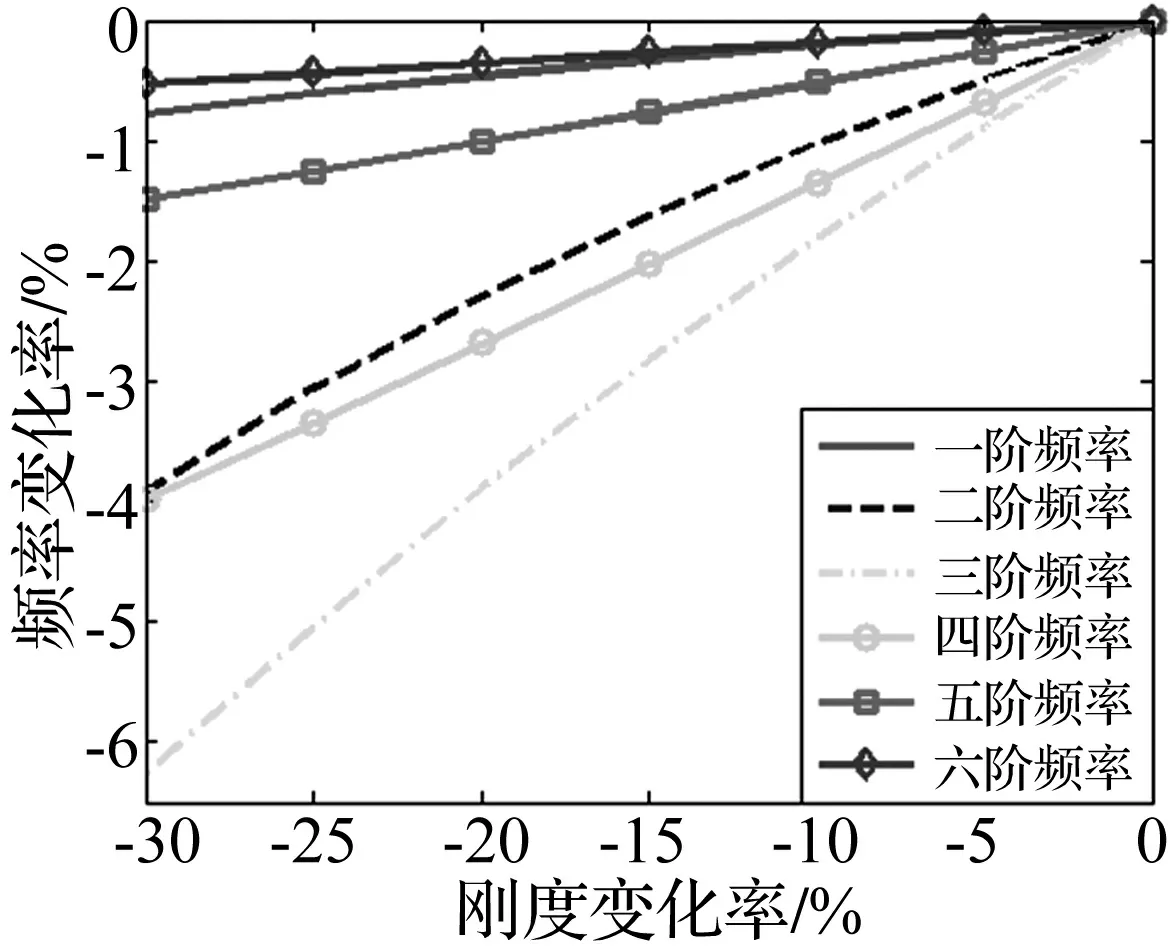
图8 简支梁单个支座出现损伤Fig.8 Influence of freq uencies with bearing damage

图9 简支梁两支座不同损伤Fig.9 Influence of frequencies with two bearings damage

6 结 论

(1) 基于Bernoulli-Euler梁理论，改进直接模态摄动方法获得完全弹性支承变截面梁动力特性的半解析解。推导出完全弹性边界条件下系数Δkki的具体计算式。算例分析表明，改进摄动法(IPM)可有效求解完全弹性支承变截面梁的动力特性，且计算精度高、收敛速度快。尤其在参数敏感性分析、计算效率方面具有有限元无法比拟的优势。

(2) 据振型对称性，对改进摄动法进行简化获得适用求解完全弹性支承变截面对称梁动力特性的简化计算方法(SIMP)。该方法不仅能减少未知系数、未知数数量约50%，且迭代次数无显著增加，计算精度与改进摄动法十分接近，效率更高。

[1] Chen D W, Wu J S. The exact solution for the natural frequencies and mode shapes of non-uniform beams with multiple spring-mass systems[J].Journal of Sound and Vibration, 2002, 255(2):299-322.

[2] 卡姆克 E,著.张鸿林，译. 常微分方程手册[M]. 北京:科学出版社, 1977.

[3] Ece M C, Aydogdu M, T A skin V. Vibration of a variable cross-section beam[J]. Mechanics Research Communications, 2007,34:78-84.

[4] Tong X, T A barrok B, Yen K Y. Vibration an alysis of Timoshenko beams with non-homogeneity and varying cross-section[J]. Journal of Sound and Vibration,1995, 186(3): 821-835.

[5] Abrate S. Vibration of non-uniform rods and beams[J]. Journal of Sound and Vibration,1995, 185(4):703-716.

[6] 钱波, 岳华英. 变截面梁横向振动固有频率数值计算[J].力学与实践, 2011, 33(6):45-49. QIAN bo, YUE Hua-ying. Numerical calculation of natural freq uency of transverse vibration of non-uniform beam[J]. Mechanics in Engineering, 2011, 33(6):45-49.

[7] 徐腾飞,向天宇,赵人达. 变截面 Euler-Bernoulli梁在轴力作用下固有振动的级数解[J].振动与冲击,2007,26(11):99-101. XU Teng-fei, XIANG Tian-yu, ZHAO Ren-da. Series solution of natural vibration of variable cross-section Euler-Bernoulli beam under axial force[J] Journal of Vibration and Shock, 2007, 26(11):99-101.

[8] Mao qi-bo. Free vibration analysis of multiple-stepped beams by using adomian decomposition method[J].Mathematical and Computer Modelling, 2011,54:756-764.

[9] Hsu J C, Lai H Y, Chen C K. Free vibration of non-uniform Euler-bernoulli beams with general elastically end constraints using adomian modified decomposition method[J].Journal of Sound and Vibration, 2008,318: 965-981.

[10] Hoskinga R J, Husaina S a, Milinazzo F. Natural flexural vibrations of a continuous beam on discrete elastic supports[J]. Journal of Sound and Vibration, 2004,272:169-185.

[11] Lou Meng-lin, Duan Qiu-hua, Chen Gen-da. Modal perturbation method for the dynamic characteristics of Timoshenko beams[J].Shock and Vibration,2005,12:425- 434.

[12] 张怀静, 潘旦光. 变截面连续梁动力特性的半解析解法[J]. 北京科技大学学报, 2008,30(6):590-593. ZHANG Huai-jing, PAN Dan-guang. Semi-analytic solution to dynamic characteristics of non-uniform continuous beams [J]. Journal of University of Science and Technology Beijing, 2008, 30(6):590-593.

[13] 楼梦麟,牛伟星. 复杂变截面梁的轴向自由振动分析的近似方法[J] 振动与冲击, 2002, 21(4):27-29. LOU Meng-lin, NIU Wei-xing. Approach for longitudinal free vibration of complicated beams with variable cross sections[J]. Journal of Vibration and Shock, 2002, 21(4):27-29.

[14] Clough R W, Penzien. J. Dynamics of structures (2nd Edition) [M].New York: Computers and Structures, Inc, 2004.

[15] 王正林，龚纯，何倩. 精通 MATLAB 科学计算[M]. 北京：电子工业出版社，2009.

[16] 叶茂,谭平,任珉,等. 中间带弹性支承各种边界条件连续梁模态分析[J]. 工程力学, 2010,27(9):80-85. YE Mao, TAN Ping, REN Min, et al. Modal analysis of multi-span beams with intermediate flexible constraints and different boundary conditions[J]. Engineering Mechanics, 2010,27(9):80-85.

[17] 宋殿义,蒋志刚,陈北雁. 弹性支承梁自振频率分析[J]. 江苏建筑, 2005(1):30-38. SONG Dian-yi, JIANG Zhi-gang, CHEN Bei-yan. Natural frequency analysis of elastic support beam[J]. Jiangsu Construction, 2005(1):30-38.

Semi-analytical solution of dynamic characteristics of non-uniform beams with complete elastic supports

YAN Wei-ming, SHI Lu-ning, HE Hao-xiang, CHEN Yan-jiang

Beijing Laboratory of Earthquake Engineering and Structure Retrofit,Beijing University of Technology, Beijing 100124, China)

The mode perturbation method was modified and the improved perturbation method (IPM) was used to solve the vibration problem of non-uniform beam with complete elastic supports based on Bernoulli-Euler beam theory. In the modal subspace of an equivalent uniform beam with complete elastic supports, the variable coefficient differential vibration equation of the non-uniform simply supported continuous beam with complete elastic supports was converted to nonlinear algebraic equations. The semi-analytical solution of dynamic characteristics of non-uniform beam with complete elastic supports was obtained and the formula of coefficient Δkkiwas given. An example analysis indicates that the improved perturbation method not only has high precision and good convergency but also considers the elastic supports effect on dynamic characteristics. A simplified calculating method (SIPM) for symmetrical beam was proposed based on the symmetry of mode shapes. The bearing damage effects on dynamic characteristics of non-uniform simply supported beam bridge were discussed.

improved perturbation method; non-uniform beam; complete elastic support; natural frequency; mode shape

国家自然科学基金项目(51378039，51378037)

2014-05-22 修改稿收到日期：2014-06-24

闫维明 男，博士，教授，博士生导师，1960年9月生

U441+.3

A

10.13465/j.cnki.jvs.2015.14.014