基于多点弯曲应变测量原理的数字式扭力扳手研究*
2015-06-09倪守忠蒋晓波
倪守忠 蒋晓波 余 融
(浙江省计量科学研究院,杭州 310013)
基于多点弯曲应变测量原理的数字式扭力扳手研究*
倪守忠 蒋晓波 余 融
(浙江省计量科学研究院,杭州 310013)
提出了基于多点弯曲应变测量扭矩的方法并通过力学分析进行了测量误差估计;在此基础上研制一种高精度数字扭力扳手并进行了实验验证。试验结果表明:研制的数字式扭力扳手,在试验力臂变动60%范围内测量误差可以控制在0.5%以内。
扭力扳手;弯曲应变;剪力干扰
0 引言
扭力扳手广泛应用于建筑、汽车、船舶及各种动力机械制造行业。扭力扳手可分成机械式和数字式两大类;按用途可分为施工用扭力扳手和测量用扭力扳手。施工用扭力扳手通常准确度在3%以下;测量用扭力扳手准确度通常在3%以上。数字式扭力扳手大多用于测量,准确度在1%~3%之间。大部分数字式扭力扳手传感器采用弯矩或扭矩测量方式进行扭矩测量,前者是一种近似扭矩测量方法,传感器的输出不仅与测量扭矩有关,还与施拧力力臂有关;后者尽管直接测量扭矩,但传感器贴片位置的局限,使传感器的抗剪切性能无法得到保证,当扭力扳手测量时对施拧力比较敏感,制约了测量精度的提高。采用多截面弯曲应变测量原理可以有效提高数字扭力扳手的测量准确度。
1 扭力扳手的结构设计及测量原理
1.1 结构设计
扭力扳手由施拧头(1)、施拧力臂(2)等组成(见图1)。其中施拧头可以加工成方头、方孔、多边头、多边孔等以便和被测量对象连接;施拧力臂分测量区(21)和非测量区(22)两部分,测量区必须用金相组织稳定性好的合金钢加工成;测量区横截面为矩形或近似矩形的对称截面;非测量区可以是测量区部分的延伸,也可以用其他任意形状的杆件与非测量区连接。在力臂测量区上下两个表面各粘贴6个应变片,将应变片按图2接成慧斯通电桥后与测量指示仪表相连。
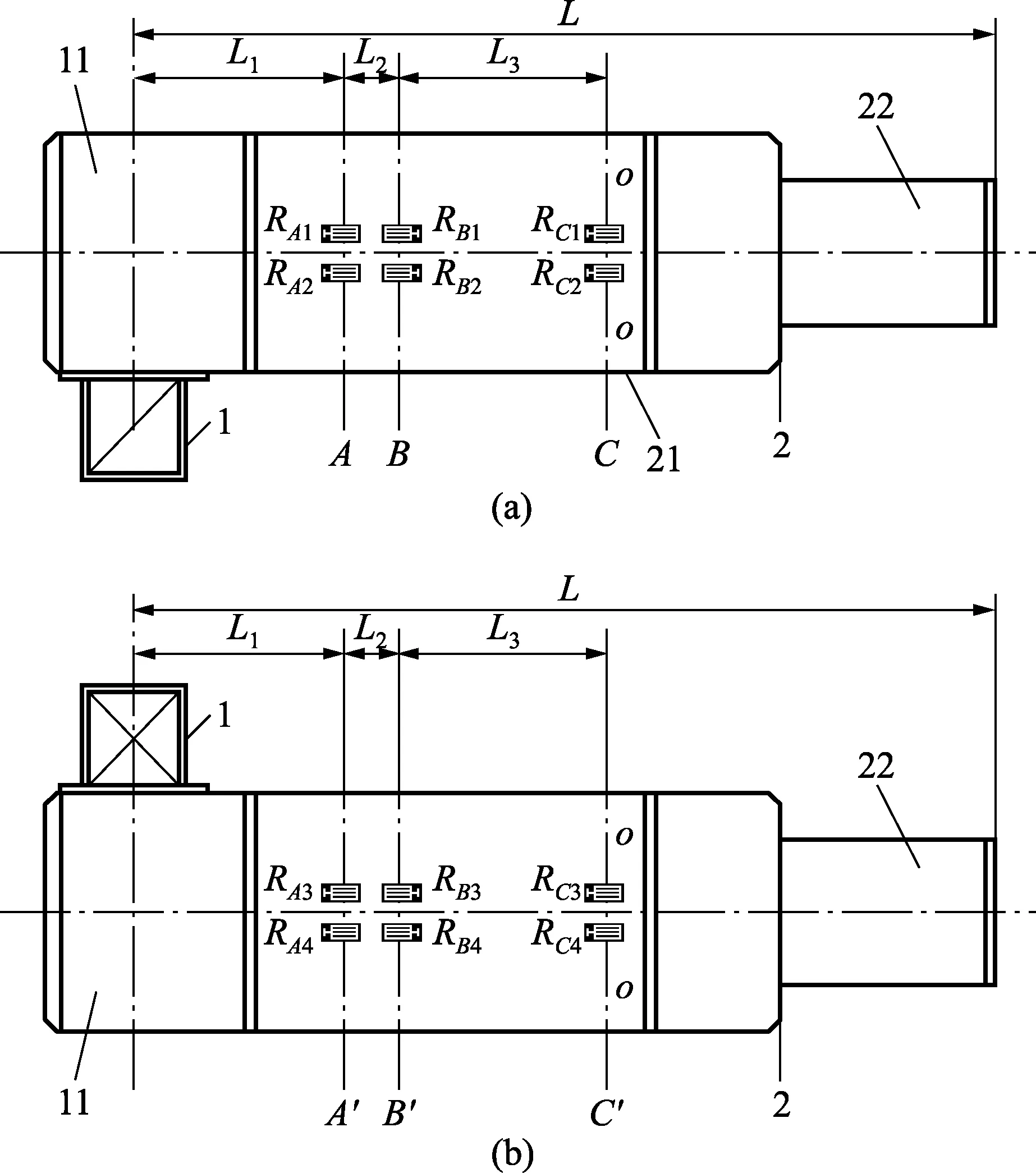
图1 结构示意图
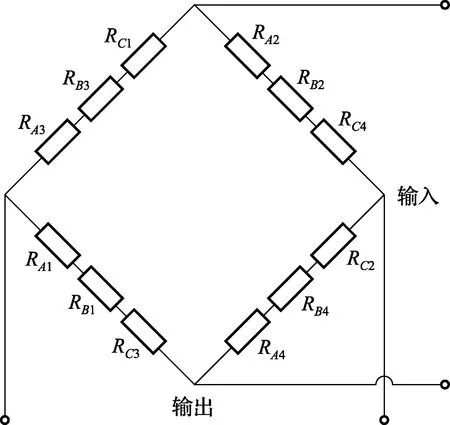
图2 测量电桥示意图
图1中,L1为A距离施拧头中心的位置,L2为B距离施拧头中心的位置,L3为C距离施拧头中心的位置;在位置A粘贴4个单轴应变片,其中上表面对称两片(RA1、RA2),下表面两片(RA3、RA4);在位置B粘贴4个单轴应变片,其中上表面对称两片(RB1、RB2),下表面两片(RB3、RB4);在位置C粘贴4个单轴应变片,其中上表面对称两片(RC1、RC2),下表面两片(RC3、RC4);各应变片按图2要求连接成惠斯通电桥。
扭力扳手需要测量的扭矩为Mn=PL,在施拧力P的作用下,力臂位置A、B、C三处的弯矩分别为:
MA=P(L-L1)
MB=P(L-L1-L2)
(1)
MC=P(L-L1-L2-L3)
假设截面的尺寸为高度h、宽度b;则对应截面的最大弯曲应力分别为:
(2)
对应截面的最大弯曲应变分别为:
(3)
式中:E为弹性模量。
1.2 单截面测量原理
常规的数字扭力扳手通常采用单截面弯曲应变测量方案,测量应变片通常粘贴在A位置,扭力扳手的输出与测量截面的弯矩成正比;扭力扳手的输出可表示成:
(4)
1.3 多截面测量原理
采用多截面测量方案时,扭力扳手的输出可表示成:
(5)
式中:K为应变片系数;Ri为传感器输入电阻;Ro为传感器输出电阻;RA=RB=RC。
令L3=L1,则扭力扳手输出可表示成:
(6)
比较式(4)和式(6),可以看出,采用单截面弯矩测量时,扭力扳手的输出不仅与扭矩Mn有关,还与长度比有关;而采用多截面弯矩测量时,扭力扳手的输出只与扭矩Mn=PL成正比。
2 扭力扳子的误差估计
2.1 单截面测量时力臂变动误差估计
假设扭力扳手使用时力臂长度从L变到L′,扭矩PL=Mn保持不变;根据式(4)可以得到两种条件下输出:
力臂变动引起的误差为:
(7)

只要L1=L3,并且合理组桥,扭力扳子在理想测量条件下的输出信号只与PL成正比;但实际上传感器应变片粘贴尺寸不可避免存在偏差,假设L1-L3=Δ1,根据式(5)可以得到:
(8)
若扭力扳手使用时力臂长度从L变到L′,扭矩PL=Mn保持不变;根据式(8)可以分别得到两种条件下输出:
力臂变动引起的误差为:
(9)
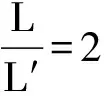
2.3 多截面测量弯曲干扰误差估计
扭力扳手在测量过程中不可避免存在与作用力正交方向的干扰力Q和N作用,由于轴力N仅产生简单压应力,与弯曲应力相比可忽略;假设各应变片粘贴时最大偏离横向中性层±Δ2,则各应变片的最大弯曲应变为:
(10)
极限干扰输出为:
式(5)不等式约束表示当馈线负荷转移后,联络线路所属变电站下所有馈线负荷之和应小于等于变电站允许最大负荷,即变电站不过载。

(11)
考虑到实际的Δ随机分布,共有12个应变片,其可能的干扰输出可估计为:
(12)
干扰输出占输出的比值为:
(13)
由于剪力Q是由于驱动力臂时角度不垂直引起,假设倾斜角度θ≤5°,则有:
Q≈Psinθ=0.087P,于是:
(14)
由此可以看出,干扰力Q引起的误差与贴片截面高度h及应变片偏离量Δ2成正比,与贴片截面宽度b的平方成反比,由于Δ2由贴片工艺决定,只要合理控制截面参数,就可以将干扰误差控制在规定的范围内。
3 扭力扳手测试比较
按上述设计思路制作了一套1000N·m数字式扭力扳手,在产品定型前暂时采用通用仪表进行扭矩指示。扭力扳手的主要设计参数及误差估计见表1。

表1 设计技术参数及误差估计
3.1 样机测试结果
将样机放在0.3级扭力扳手检定仪上,分别在60%、80%和100%三个力臂进行测试(见图3),测试结果见表3。

图3 扭力扳手试验
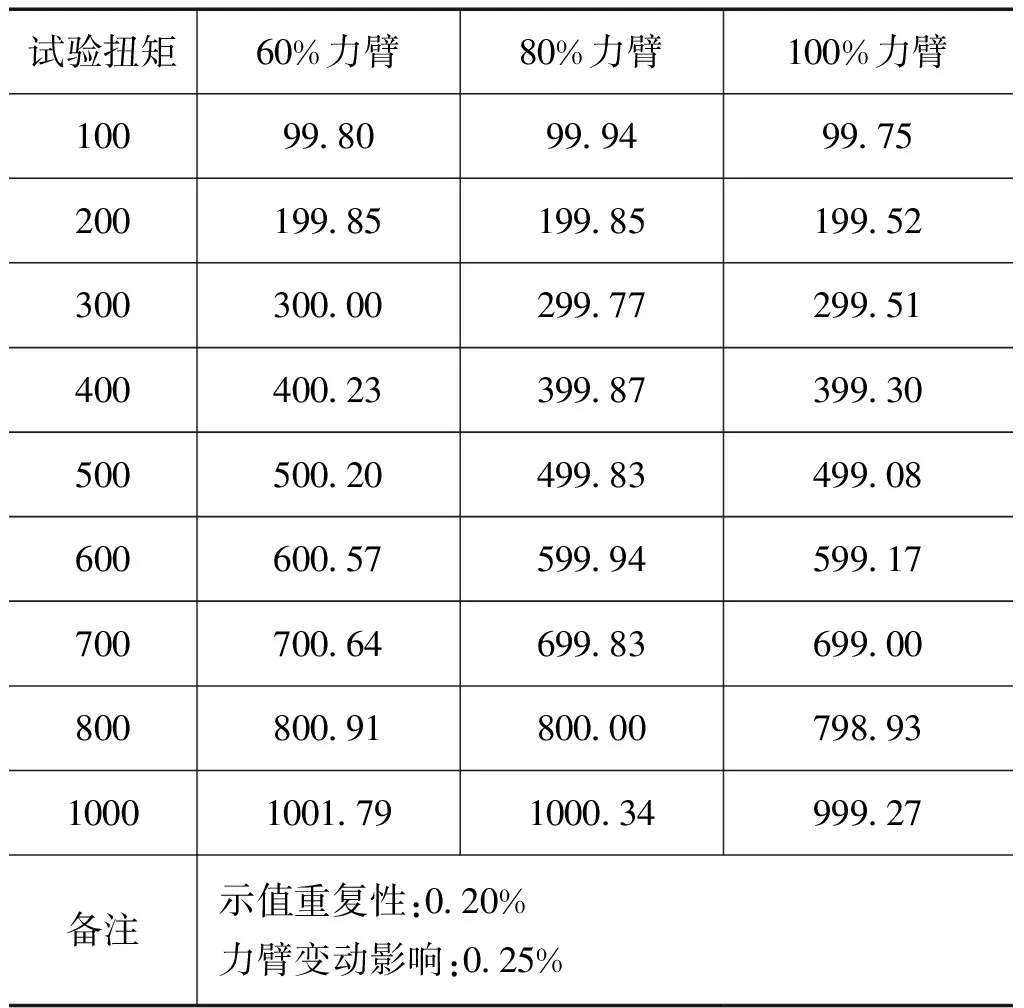
表3 样机测试数据 N·m
3.2 普通扭力扳手测试结果
为了进行比较,我们选择国产和美国进口扭力数字扳手各一把,在美国CDI扭力扳手检定仪上进行对照试验,试验项目包括示值误差、示值重复性、力臂变化影响(见表4、5)
测试结果表明:通过测量多点弯曲应变技术制作的数字扭力扳手力臂变动引起的误差远小于普通数字扭力扳手的测量误差。
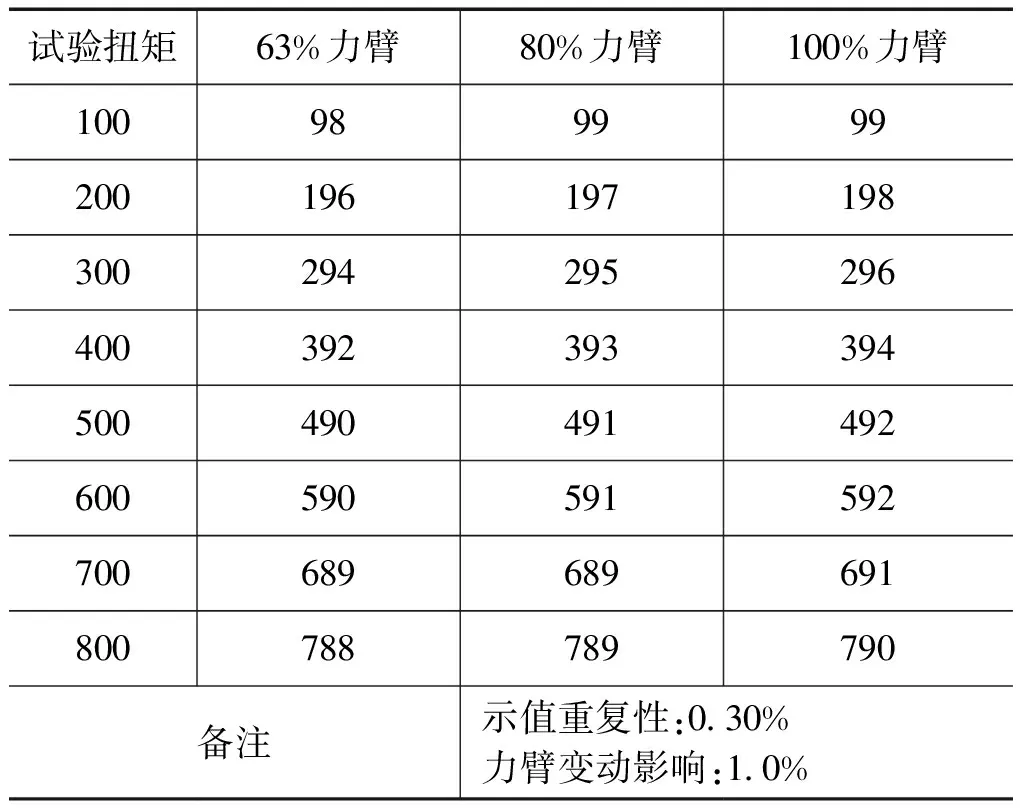
表4 某进口数字扭力扳手测试数据 N·m
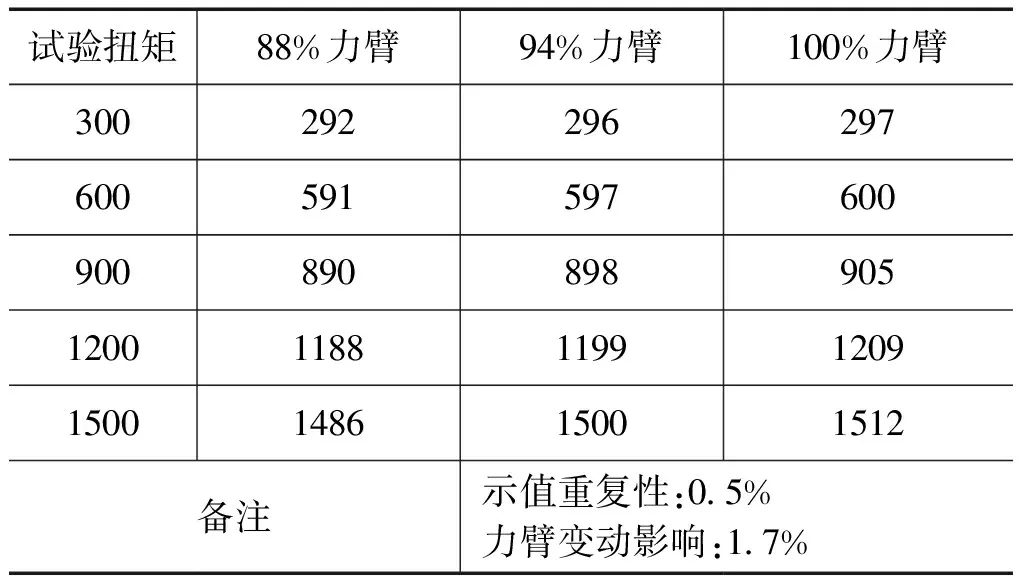
表5 某国产数字扭力扳手测试数据 N·m
4 结束语
提高数字扭力扳手的测量准确度与降低其制造成本是扭矩计量领域急需解决的一个技术难题。理论分析和实验结果表明,通过测量多点弯曲应变结合电桥补偿技术,可以在简单结构设计的条件下有效解决力臂变化对数字式扭力扳手的干扰影响的技术难题,提高扭矩测量准确度。
[1] GB/T 15729—1995扭力扳手通用技术条件[S]
[2] JJG 707—2003扭矩扳子[S]
[3] 倪守忠.一种数字式扭力扳手[P]:中国,201220601819.X.2012-11-14
[4] 胥凯晖.一种数字式扭力扳手检定装置[J].计量与测试技术,2009(5):14-16
[5] 陆耀祖.扭矩型扭力扳手验收的探讨[J].组合机床与自动化加工技术,2000(3):39-42
[6] 张家全.检定扭力扳手的新方法和要求[J].计量技术,1995(12):29-33
*浙江省计量科学研究院科研计划项目(2012YL201)
10.3969/j.issn.1000-0771.2015.2.05
