基于Simulation对转炉倾动装置扭力杆的有限元分析

张皓天

（太原重型机械集团，山西 太原030024）

0 引言

转炉倾动装置是实现转炉炼钢生产的关键设备，它在转炉炼钢设备中对炉体起到平稳倾翻和准确定位的作用。当炉体在进行加料、出渣、拉碳、出钢和补炉等一系列工艺操作时需要通过倾动机构所产生的扭矩来使转炉进行转动。倾动装置为整套设备提供动力，其重要性可见一斑。其工作特点是低速、重载、启制动频繁、速比大、工作条件恶劣并且受冲击非常大。扭力杆作为倾动装置的一个关键部件，它可以在倾动运行时起到抗扭缓冲的作用，这对保证设备运行安全平稳、延长设备寿命是非常重要的。其具体的工作原理为：在一二次减速机与炉体作为相对静止的设备绕耳轴转动时，安装在二次减速机下方左右两侧的的两个联接杆一个受拉，一个受压，再将力传递给扭力杆两侧的曲柄装置，并在扭力杆两侧形成大小相等方向相反的一对力偶，使得扭力杆发生弯扭变形，从而对倾动设备起到支撑、抗震缓冲的作用。为全面了解扭力杆的变形及应力分布状态，确定其刚度与转角是否符合设计安全，并提供直观的分析计算报告，特应用Solidworks中的Simulation有限元分析模块对扭力杆进行了分析研究。

1 转炉倾动装置结构

如图1所示转炉倾动装置主要由一次减速机、二次减速机、扭力杆、电机等部分构成。倾动装置现主要采用全悬挂式结构。它的特点是整个倾动装置全部挂在托圈的传动侧耳轴上，四台一次减速机末级齿轮同时驱动二次大齿轮转动，二次大齿轮通过切向键传递扭矩到耳轴上面从而驱动托圈炉体绕耳轴中心线转动，进而完成兑钢水、加废钢、取样、出钢和倒渣等操作。为了防止倾动机构输出扭矩时同时绕着耳轴中心线转动，在二次减速机下方安装有扭力杆装置，并通过左右联接板与二次减速机箱体联接，这样扭力杆装置就可以对整个机构起到支撑的作用。当炉体进行转动时，倾动机构的回转动能，在扭力杆进行支撑和缓冲的过程中，经连接板转变为扭力杆的扭转变形能。

图1

2 Simulation软件

Simulation是DSSolidworks公司开发的一款基于有限元技术的设计分析软件，同时它作为嵌入式软件可以做到与Solidworks无缝集成。

3 扭力杆的常规计算

扭力杆的安全与否对整套设备的安全与稳定起着非常重要的作用，所以对扭力杆强度进行校核是非常有必要的。此处我们以某钢厂300t转炉倾动(图1)为原型进行分析，已知该倾动的最大倾动力矩为6500kN*m，联接杆中心距离扭力杆中心距离S为560mm，扭力杆曲柄宽160mm，扭力杆最小轴径380mm。

（1）我们在对扭力杆进行分析时需要建立力学模型，如图2所示：作用在曲柄上的拉力与压力可以等效成作用在扭力杆曲柄C点与曲柄D点的力FC、FD和扭矩TC、TD的叠加。

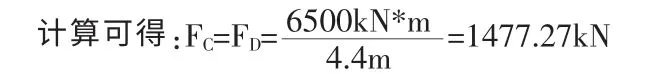
图2

（2）CD之 间 的 扭 矩 为：T=-FC*S=FD*S=-1477.27kN*0.56m=827.27kN*m

做扭矩图，如图3所示：

图3

（3）根据弯矩平衡计算轴承座A、B处受力FA*5380+FC*4890-FD*490=0

FB与FA大小相等，方向相反FB=1208kN

（4）C点所受弯矩MC=-FA*0.49m=-1208kN*0.49m=-591.92kN*m

D点所受弯矩MD=FB*0.49m=1208kN*0.49m=591.92kN

做弯矩图，如图4所示：

图4

可见在C点与D点，扭力杆的所受的弯矩与扭矩最大，所以这两点变形位移量也是最大的。

（5）根据第四强度理论，在C点与D点，扭力杆的当量弯矩

式中：σp为许用应力，其中40Cr调质钢的需用应力此时取值为172MPa

该模型扭力杆曲柄处轴径为580mm，远远大于许用值，符合要求

式中：T为扭矩，T=827.27kN*m；L为有效变形长度，L=4400-160=4240mm；G为扭转弹性模量，G=8.1*104N/mm2；J为抗扭惯性距，J=Πd4/32=2.046*109mm4

d取该扭力杆最小轴径380mm

代入该公式得φ=0.021rad=1.2°（小于最大需用扭转角度3°），符合要求

故该扭力杆的设计是符合要求的。

以上为扭力杆强度校核的常规算法，该方法公式较多，计算较为复杂，同时不能够直观的看出扭力杆的应力分布状态。

4 扭力杆的有限元分析

此处我们利用Solidworks软件中的自带插件Simulation对扭力杆进行有限元分析。

首先，依据图纸进行建模，如图5所示。由于扭力杆与联接板采用键销联接，故此处我们将其当成整体。

图5

其次，进入Simulation界面对扭力杆开始进行有限元分析操作。

（1）规定扭力杆材料

（2）加载力以及添加约束条件。由于扭力杆同时受扭矩和弯矩的作用，我们把扭力杆一侧设为固定约束，另一侧约束为可以自由转动的轴承约束。然后在扭力杆轴承约束侧联接板处加向下压力，力大小为FC=FD=1477.27kN。如图6所示：左侧为固定约束，右侧为轴承约束。

图6

（3）划分网格，如图7所示。

（4）有限元分析运算，得出结果。

图8为扭力杆的应力分布图。由图8我们可以看到：扭力杆的应力分布式呈现对称状态的，并且在扭力杆中心处的应力是非常大的，但是最大应力显示却不在靠近中心的位置，反而出现在靠近扭力杆曲柄的位置处，这是因为在靠近扭力杆曲柄位置处的设计圆角半径不够大从而产生了应力集中所导致的，这样经过分析，我们还可以直观的发现在扭力杆设计细节的不足之处，从而做出改进（增大过渡圆角）。

图7

图8

图9为扭力杆的位移图，由图我们可以得出扭力杆的最大为位移处为曲柄的最外缘处，最大位移为20mm，这也与扭力杆实际情况下的位移状态是相符的。通过位移量换算为偏转角度为φ=1.25°。这与之前验算的偏转角φ1.2°是相符的。从另一方面也验证了扭力杆有限元分析的正确性。这样我们也可以得出扭力杆的设计是符合要求的。

图9

5 结论

以上我们介绍了扭力杆分析计算的两种方法，通过比较我们可以发现基于Simulation软件对扭力杆进行分析计算不仅更加快捷简单而且更加直观，可以很形象很准确的为我们设计扭力杆提供理论依据。

［1］机械设计手册[M].化学工业出版社.

［2］刘鸿文.材料力学[M].高等教育出版社.