水平陪检标准器镜面倾斜量测量方法的探讨*

2015-06-09刘素洁王蔚晨李张标

计量技术 2015年2期

关键词：镜面棱镜液面

刘素洁丁晨王蔚晨李张标

(1.宁波市计量测试研究院，宁波 315048；2.安徽省计量科学研究院，合肥 230051；3.中国计量科学研究院，北京 100029)

水平陪检标准器镜面倾斜量测量方法的探讨*

刘素洁1丁晨2王蔚晨3李张标

(1.宁波市计量测试研究院，宁波 315048；2.安徽省计量科学研究院，合肥 230051；3.中国计量科学研究院，北京 100029)

通过对水平陪检标准器机械结构的分析，得知引起水平陪检标准器(又名吊镜)镜面倾斜的因素，并对吊镜在不同摆位摆动时不同因素的影响做了分析，同时利用数学模型对这些影响因素进行推导，结合实验数据计算出吊镜摆差和转动轴倾斜引起的镜面倾斜角度，并溯源到水平面。最后对测量过程中影响不确定度的因素进行了分析。

计量学；水平面；水平准线；水平陪检标准器；五棱镜；自准直仪

0 引言

水平陪检标准器因其准确度高、便于携带的特点，而被作为水平传递标准应用于水准仪检定装置的现场检测[1]。水平陪检标准器(以下简称吊镜)的溯源一直是角度计量需要解决的问题之一，现有文献中也鲜有就其自身误差进行分析的文章。

长久以来人们总是将吊镜内部的双面反射镜默认为是铅垂的，两个反射面是平行的，而并未对其进行溯源。但实际由于吊镜的机械结构和加工误差等原因，存在若干个引起镜面倾斜的因素，使得双面反射镜并非铅垂，两个镜面也并非完全平行，以此为水平传递标准也将会引入一定的系统误差，对检定结果产生一定的影响，因此对吊镜进行溯源也就显得尤为必要[2-3]。

1 吊镜的结构及其自身的影响因素分析

要对吊镜进行溯源，首先得确定引起吊镜镜面倾斜的因素有哪些，图1是吊镜结构示意图。

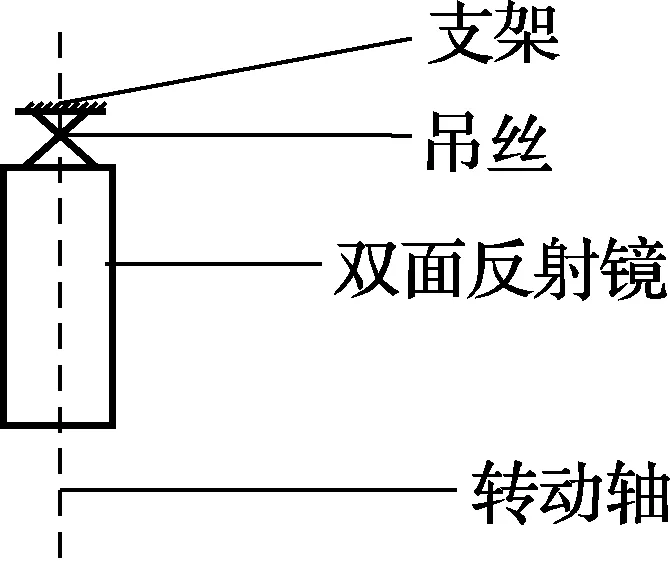
图1 水平陪检标准器的结构示意图

双面反射镜从理论上来说两个反射面是平行的，但实际由于加工问题，使其存在一个微小的角度，俗称楔角，记为a 。支架的不完全水平以及双面反射镜自身的偏重都使其与铅垂方向存在一个角度，但是由于这两个因素引起的角度在吊镜转换摆位时方向变化一致，因此合并为一个参量，定义为摆差，记为β。由于机械加工和装配的因素，转动轴也并非铅垂，因而将由转动轴倾斜引起的镜面与铅垂线的夹角记为δ。

2 吊镜自身影响因素的运算及推导

2.1 实验过程及原理分析

将2台自准直仪共轴放置，中间放置一个转台，转台上固定五棱镜，在五棱镜下方放置一盛有液体的容器，如图2所示。自准直仪发出的光经五棱镜到达液面，从液面反射后又回到自准直仪，将自准直仪的结果清零，利用转台旋转180°，使另一台自准直仪也读出液面的读数，然后将结果清零。

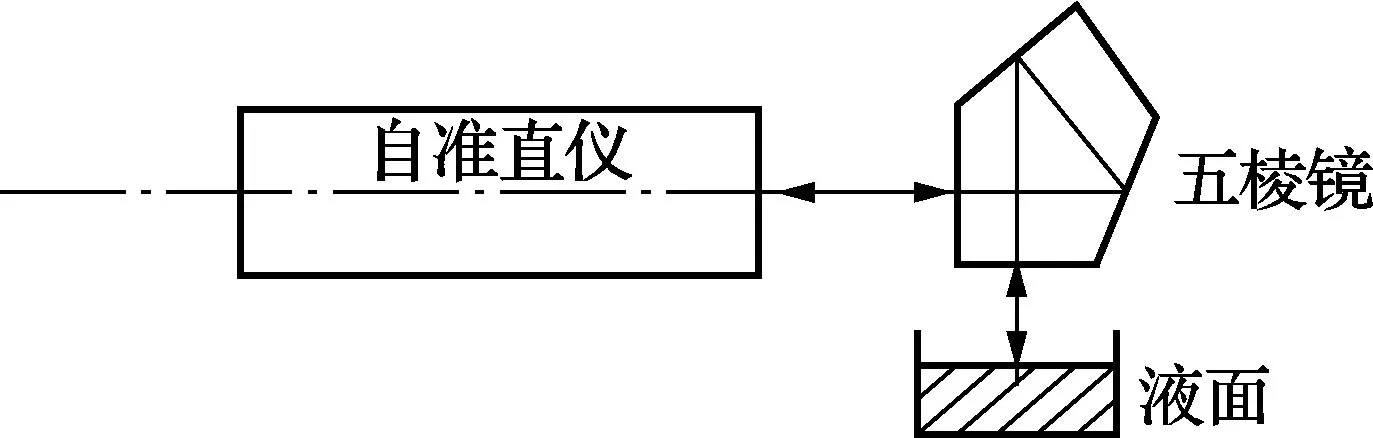
图2 自准直仪测液面原理图

移出五棱镜，将吊镜放入自准直仪中间，自准直发出的光经平面镜反射后回到自准直仪，其原理图如图3所示。

图3 自准直仪测吊镜摆差原理图

自准直仪的读数受a ，β，δ的影响如表1所示(假设此处的β，δ均与铅垂线成顺时针夹角)。

表1 吊镜变换摆位时各影响因素的变化

五棱镜是光学仪器中比较常用的一种反射棱镜，它的光学特性是可以将入射光线偏转90°，而且对棱镜的定位精度要求不高[4]。而液体因为具有流动性使其无论怎么放置其表面总能处于水平状态，这是自然界赋予的水平的自然基准，所有与液面垂直的直线都是铅垂的。但是由于五棱镜加工误差的存在，使得液面的反射光线通过五棱镜后并非完全垂直，而是与水平面存在一个微小的角度，记为ε，在自准直仪的读数中作为系统误差存在，无法消除。

2.2 各影响因素的运算及推导

将吊镜摆Ⅰ时，两台自准直仪的读数分别定为A1，A2；摆Ⅱ时，分别定为B1，B2。基于上述分析，可得到以下4个方程式：

A1=a /2+β+δ+ε

(1)

A2=a /2-β-δ+ε

(2)

B1=a /2-β+δ+ε

(3)

B2=a /2+β-δ+ε

(4)

式(1)-(3)可得

A1-B1=2β，则β=(A1-B1)/2

(5)

式(4)-(2)可得

B2-A2=2β，则β=(B2-A2)/2

(6)

式(1)-(2)可得A1-A2=2β+2δ,将式(5)代入后解得

δ=(B1-A2)/2

(7)

式(4)-(3)可得B2-B1=2β-2δ,将式(5)代入后解得

δ=(A1-B2)/2

(8)

式(5)式(6)和式(7)式(8)是否相等可用来验证上述4个方程式。

3 实验数据处理

此实验中采用的自准直仪为德国MOLLER公司生产的ELCOMAT3000型光电自准直仪(分辨率为0.005″)，五棱镜经中国计量科学研究院检定其内角误差小于等于0.1″，吊镜为中国地震局地震研究所研制的JSJ-PB水平标准陪检器，实验设备摆放如图4和图5所示。

图4 自准直仪通过五棱镜测液面

图5 自准直仪测吊镜不同摆位

将上述实验中两台自准直仪的读数记录在表2中。

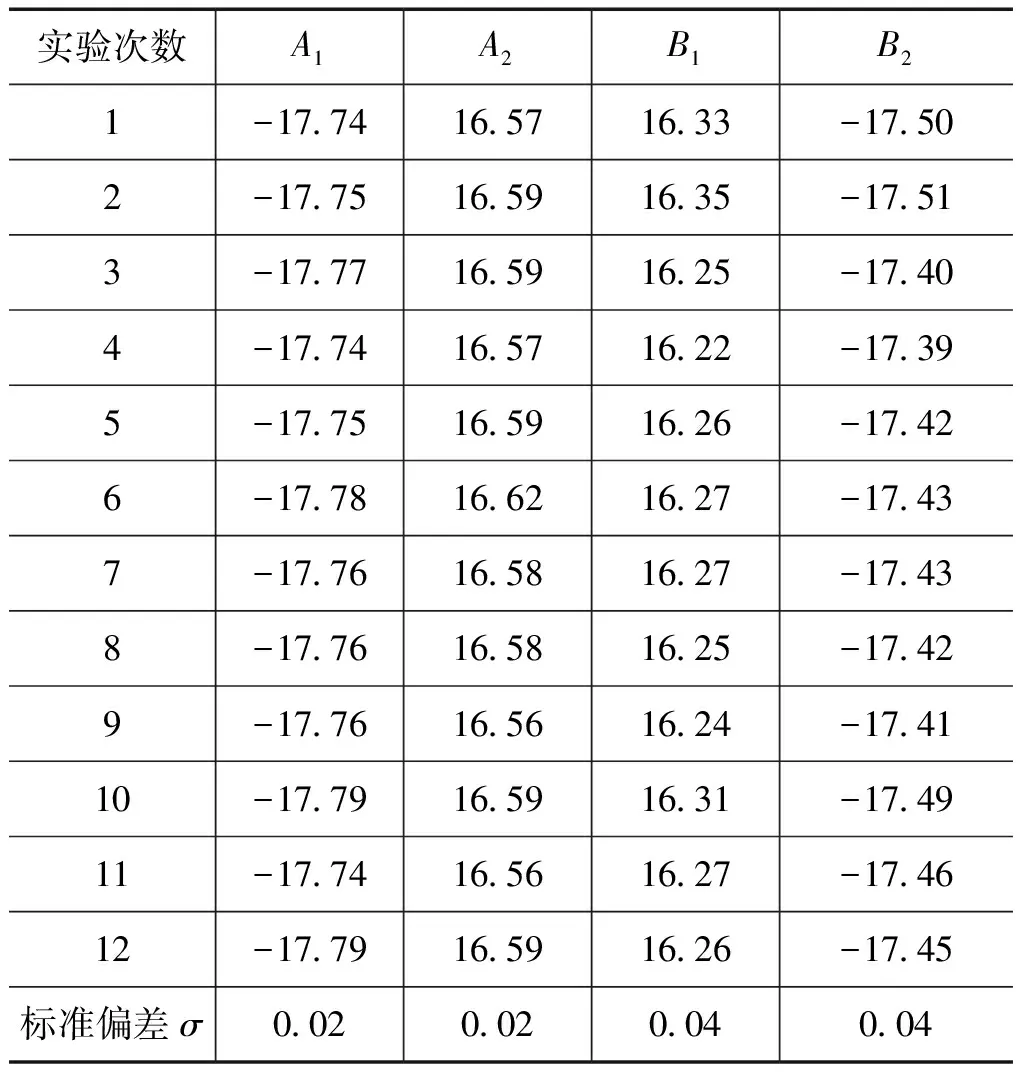
表2 自准直仪测吊镜记录数据单位：″

将表2中的数据分别代入式(5)～(8)中，解得β和δ值如表3所示。

表3 解得的β和δ值单位：″

表3中的β和δ变化趋势图分别如图6和图7所示。

图6 摆差β变化趋势图

图7 转动轴引起的镜面倾斜角δ变化趋势图

由图6、7可知，不同方程式得到的β和δ值都非常接近，两者之间的差值均小于0.02″，考虑到实验中的随机误差存在，可认为式(5)、(6)解得的β相等，式(7)、(8)解得的δ相等。另外由于β和δ均为负，可知摆差和转动轴引起的镜面倾斜方向均在铅垂线的逆时针方向，大小分别为17.02″和0.16″。

4 影响测量不确定度的主要因素

上述实验是在20.0℃,50%RH的环境下进行，影响实验结果的因素主要有：

1)水平是否稳定。水平面(即液面)稳定主要取决于环境(这里主要指气流)和地基的影响。因此实验设备用保温罩封闭以减小外界气流的影响，放置实验装置的大理石平台也单独位于隔振楼的隔振地基之上。

2)自准直仪是否稳定。实验中用的是德国MOLLER公司生产的ELCOMAT3000型光电自准直仪，该自准直仪精度在1″范围内为0.02″，10″范围内为0.03″。另外通过对自准直仪的短期稳定性实验可知，一个小时内自准直仪的读数标准差为0.03″。

3)五棱镜的内角加工误差。五棱镜结构图如图8所示。

图8 五棱镜结构图

理想情况下，ω=90°，θ=45°，从五棱镜一个面进入的光线经过五棱镜后会转折90°出射，而出射光与入射光间的夹角不随入射角的变化而变化，该夹角总是90°。因此在五棱镜转动180°的过程中，转台的倾斜并不会引起五棱镜出射角度的变化。但实际上五棱镜的内角存在加工误差，实验中所用的五棱镜经测定内角误差小于等于0.1″，因此由五棱镜加工误差引起的转向角变化量可忽略[5-7]。