基于方位向门限的FMCW MIMO雷达波束形成成像算法

2015-06-05杜东贞段海涛

系统工程与电子技术 2015年12期

关键词：旁瓣门限方位

王伟，梁栋，刘琦，杜东贞，段海涛

（哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

基于方位向门限的FMCW MIMO雷达波束形成成像算法

王伟，梁栋，刘琦，杜东贞，段海涛

（哈尔滨工程大学自动化学院，黑龙江哈尔滨150001）

针对传统波束形成算法的旁瓣效应在调频连续波多输入多输出（frequency modulated continuous wave multiple-input multiple-output，FMCW MIMO）雷达的成像结果中造成的方位向虚警问题，提出了一种基于方位向门限的改进成像算法。首先从原始数据中分别提取目标的距离向、方位向信息，然后单独将方位信息归一化之后使用门限检测实现了对方位向虚假目标的抑制，最后结合距离向信息与方位向信息得到了成像结果。仿真成像实验证明，该方法能使得成像结果中的虚警概率明显降低，外场实验的成像结果进一步验证了所提出算法出色的成像性能。

多输入多输出雷达；调频连续波；波束形成；虚警；外场成像实验

0 引言

作为一种新兴的雷达体制［1］，多输入多输出（multipleinput multiple-output，MIMO）雷达在21世纪之初被正式提出之后就立即受到国内外众多学者和研究机构的广泛关注［25］。MIMO雷达的多发多收体制可以等效为一个独立收发的虚拟阵列使得其方位分辨率明显高于实孔径雷达。调频连续波（frequency modulated continuous wave，FMCW）是一种宽带雷达的信号体制，既具有连续波雷达的小功率的特点，又具有脉冲雷达的测距能力［6］。MIMO雷达成像技术是MIMO雷达的等效虚拟阵列技术与宽带雷达成像处理相结合的产物，由于MIMO雷达的信号可以通过时间分集来实现理想正交，以时分正交的方式发射接收FMCW信号的FMCW MIMO雷达成为较为流行的MIMO雷达成像实现方案［7-11］。

成像算法作为雷达成像技术中的关键一环，决定着成像分辨率、实时性等重要指标。文献［7］提出了一种在距离向和方位向同时使用子空间超分辨率技术的成像算法，得到了较为理想的成像结果。然而空时二维平滑后矩阵庞大的维数和距离、方位的二维搜索使这一算法需要庞大的运算量，难以被用于实时成像。而且子空间类算法应通常依赖于一些先验信息如目标的个数、相关性等［8］，使得这些算法在实际使用前需对原始数据进行必要的预处理，这不仅进一步增加了算法所需要的运算量，而且降低了整个系统的鲁棒性。波束形成是阵列信号处理、智能天线系统中的一项重要技术，既可以估计信源数也可以估计目标的方位，对于含有不确定因素的模型拥有很强的鲁棒性［1213］。然而从文献［7- 11］所给出的MIMO雷达波束形成算法的成像结果中可以看到，旁瓣效应使得在与目标的同一距离向的其他方位的位置上出现了一系列的虚假目标，这些虚假目标造成了雷达虚警的同时也影响了一些真实目标的辨识。

针对上述问题，本文首先分析了常规波束形成算法旁瓣在成像结果中产生虚假目标的原因，然后在经典波束形成算法的基础上提出了一种基于方位向检测门限的改进算法。该算法通过预先分离目标的距离信息和方位信息，再单独对方位向数据归一化后施加检测门限来消除旁瓣在成像结果造成的不良影响。对多目标成像的仿真实验验证了该算法对虚假目标的抑制能力，对外场实验实测数据进行处理所得的成像结果表明，该算法使雷达对目标的识别和分辨的能力大大提高，具备良好的实用性。

1 FMCW MIMO雷达系统模型

单基地共址MIMO雷达的发射阵列以时分的方式发射FMCW信号，阵列中的第i个天线的发射信号为

式中，VT为信号的幅值；f0为FMCW信号扫频的起始频率；φ0表示信号的初始相位；T为信号的扫频周期；B为信号的扫频带宽。

MIMO雷达的等效虚拟阵列［14］如图1所示，将虚拟阵列的几何中心设为雷达的距离参照点。

图1 MIMO雷达虚拟阵列与信号收发模型

图1中，R为目标距离阵列天线的距离；θ0为目标方位；xij为第i个发射天线与第j个接收天线的虚拟阵元至距离参考点的间距。假设目标位于阵列的远场，回波信号被接收阵列中的第j个天线接收，则信号传播的时间为

式中，c是电磁波传播速度。第j个接收天线接收到的回波信号为

式中，A表示信号在传播路径中的衰减以及收发天线的增益。rij（t）与si（t）进行混频后经过低通滤波器进行滤波得到中频信号：

式中，Vij为中频信号的幅值，由于在实际情况中满足f0≫B且T≫τij，式（4）可以简化为

2 波束形成成像算法

对中频信号进行采样得到离散采样序列：

式中，Ts为采样间隔；L为采样点数。对uij（n）计算L点的DFT并取单边谱为

谱峰位于k处：

设MIMO雷达拥有M个发射天线和N个接收天线，利用式（9）的结果使用波束形成方法计算目标的方位：

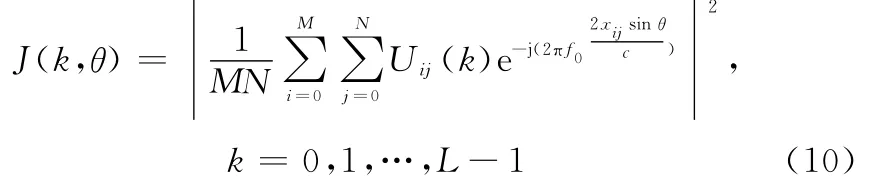
由于在式（9）中，Uij（k）在k最接近处取得谱峰，可知k对应于目标的距离R。因此，J（k，θ）即为距离为R，方位为θ处目标的回波功率。根据成像区域选取k与θ的取值范围并依次对J（k，θ）进行求取，即得到FMCW MIMO雷达波束形成算法的成像结果。

3 消除虚假目标的改进成像算法

3.1 方位向旁瓣产生虚假目标

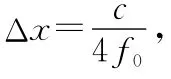
图2 目标回波功率比较

从图2所示的两幅图中可以看出，图2（a）中最高旁瓣的功率为－3.147 d Bm已然超过图2（b）中目标的主瓣功率值。图3给出了对以上2个目标使用常规波束形成算法进行成像的仿真结果。

图3 方位向旁瓣造成的成像虚警

由图3可见，旁瓣效应产生了虚假目标，使得回波功率较弱的真实目标在成像结果中已经无法通过色彩的明亮程度来鉴别，目标回波信号动态范围的增大会使这一现象所造成的影响进一步恶化，雷达成像结果的可信度将会随之变差。

3.2 方位向检测门限消除旁瓣的影响

对空间匹配滤波器的权矢量进行锥化处理可以产生更低的旁瓣，然而其代价是主瓣的展宽致使方位分辨率下降［15］。针对3.1节所提出的问题，现采取一种新的方式对数据进行处理。定义幅值函数：

剩余相位函数：

将式（12）带入式（9）并归一化得：

假设θ0＝0°，对式（11）进行均匀加权求和得目标的幅值归一化空间谱：

图4给出了相应的幅值归一化空间谱曲线，与阵列的静态方向图吻合。

图4 幅值归一化空间谱

对于阵元数目确定的均匀线阵，如图4所示，最高旁瓣的归一化幅值为确定值约为0.22。考虑到实际情况中的噪声影响以及其他干扰因素，将归一化门限电平设为l＝0.3。门限电平结合式（11）将被用来重新决定幅值函数的取值：

事实上，幅值函数携带了目标的距离信息，其最终取值由目标回波信号的幅值来决定。最终成像数据的获取需要将目标的方位信息与距离信息进行重新组合，而式（16）的结果即为距离刻度为k，方位为θ处目标的回波功率。

对于雷达系统来讲加入检测门限会牺牲雷达对低于门限电平目标的检测能力，使雷达的动态范围下降。然而根据雷达方程［16］，回波功率与目标的雷达截面积成正比与目标距离的四次方成反比，也就是说使回波信号功率动态范围变大的主要因素是目标的距离范围。前文所提出的门限检测仅仅作用在同一个距离向范围内，所有参与门限检测的目标信号功率起伏平缓，而目标能否通过门限仅取决于目标的雷达截面积，这样就使得门限的加入对雷达目标检测性能的负面影响大大降低。值得注意的是，对各个距离向的数据采取了归一化处理，使得门限电平的取值不必随着目标距离的不同而做自适应的改变，这也降低了算法的复杂度，让算法变得易于实现。

4 成像仿真与外场实验结果

为了验证本文提出方法对之前所述问题的解决效果，现进行多目标成像仿真实验，目标信息如表1所示。

表1 目标信息

仿真实验中，收发天线个数M＝N＝4，采样数L＝824。设定信噪比为10 dB，对采样数据加入高斯白噪声，然后分别使用常规波束形成算法和本文所提出的基于方位向门限的改进成像算法对目标进行成像，成像结果如图5所示。

图5 成像仿真实验对比

现分析并比较图5中两种算法的成像结果。在50 m距离向上只有一个目标，对比图5（a）和图5（b）可以看出，在使用了检测门限后目标1附近由旁瓣造成的虚假目标被成功剔除。在65 m距离向上存在2个目标，其中目标3的回波幅值较低，信号的信噪比条件较差，在图5（a）中目标3的成像结果混杂在目标2的旁瓣中难以分辨，而在图5（b）的雷达图像中，可以清楚地分辨这2个目标。在80 m距离向上有3个目标，其中目标4的回波信号较弱而目标5和目标6的回波信号较强，在图5（a）中的80 m距离向处，可以看到由于目标5和目标6的旁瓣件发生干涉干扰，致使该距离向上的雷达图像显得杂乱不堪，而在图5（b）中目标4～目标6均清晰呈现。由此可见，本文提出的算法在低信噪比条件下以及多目标位于同一距离向的情况下依然适用。

为了进一步验证文中提出方法的实际性能，设计了完整的MIMO雷达成像实验系统并进行了外场成像实验。MIMO雷达天线阵列使用了平板定向天线作为基本的收发单元，通过4个发射天线和4个接收天线可以产生阵元数为16的虚拟阵列，阵列布局方式如图6所示。

图6 MIMO雷达阵列

MIMO雷达成像实验系统如图7所示。其中，图7（a）所示的雷达信号收发机采用时分的方式发射和接收FMCW信号，通道之间的切换使用了2个射频开关来完成。图7（b）给出了完整实验系统的照片，雷达中频信号经模拟数字转换采样后被送入PC机进行处理。

图7 MIMO雷达成像实验系统

外场成像实验场地是大小约为70 m×50 m的一个广场，广场的背后为空旷的足球场，与广场之间以金属围栏相隔，如图8所示。其中，图8（a）为鸟瞰图由卫星拍摄，经黄色实线所框选的区域为雷达成像范围，图8（b）为平视图，摄像视角为雷达天线阵列的正前方，两幅图中都已对主要目标进行标注。

图9给出了常规波束形成算法和本文提出的改进算法的成像结果。

图8 外场成像实验场景参照

图9 外场实验成像结果

参照图8所示的实验场景，从图9两种算法的成像结果可以看出，在所设定的成像场景中，方位向检测门限的加入使得成像结果中的真实目标从真假目标混杂的图像中剥离，在图9（b）成像结果的右侧，可以清楚地确认广场右侧两灯柱以及花丛的位置，虚假目标的消除使围栏的成像结果连成一条直线，围栏后的足球球门甚至可以清楚地被识别。

5 结论

波束形成算法用于FMCW MIMO雷达成像具有鲁棒性强、实时性高的优点，然而其旁瓣效应使得成像结果中易出现虚假目标，限制了其实用性。针对这种情况，本文提出了一种改进的波束形成算法，将目标的方位向信息进行单独提取，采用检测门限对真实目标进行筛选，从而有效地弥补了上述缺陷。对多个点目标成像的仿真实验验证了该算法的预期性能，MIMO雷达外场实验的成像结果更加证实了该算法的实用性与可靠性。本文采用了降低雷达虚警率的途径来提高成像效果，并未对雷达的测距分辨率或测向分辨率进行提高。然而，若将超分辨率处理技术与本文所提出的方法相结合必定能够再一次改善MIMO雷达的成像性能，值得进一步研究。

［1］Fisher E，Haimovich A，Blum R，et al.MIMO radar，an idea whose time has come［C］∥Proc.of the IEEE Radar Conference，2004：71- 78.

［2］Zhang X Y，Liao G S，Xu J W，et al.Waveform design for MIMO radar to improve target detection and parameter estimation［J］.Systems Engineering and Electronics，2014，36（8）：1494- 1499.（张向阳，廖桂生，许京伟，等.提高MIMO雷达检测和参数估计性能的波形设计［J］.系统工程与电子技术，2014，36（8）：1494- 1499.）

［3］Rankin G A，Tirkel A Z，Bui L Q，et al.Radar imaging：conventional and MIMO［C］∥Proc.of the Communications on Electronics，2012：171- 176.

［4］Zhang W，He Z S，Li J.Optimization design of MIMO radar sparse array［J］.Systems Engineering and Electronics，2013，35（2）：299- 303.（张伟，何子述，李军.MIMO雷达稀疏阵优化设计［J］.系统工程与电子技术，2013，35（2）：299- 303.）

［5］Brookner E，Raytheon C.MIMO radar demystified and where it makes sense to use［C］∥Proc.of the IEEE International Symposium on Phase Array Systems&Technology，2013：399- 407.

［6］Kim S，Paek I，Ka M.Simulation and test results or triangular fast ramp FMCW waveform［C］∥Proc.of the IEEE RadarConference，2013：1- 4.

［7］Belfiori F，Rossum W，Hoogeboom P.2D-MUSIC technique applied to a coherent FMCW MIMO radar［C］∥Proc.of the IET International Conference，2012：1- 6.

［8］Feger R，Wagner C，Schuster S，et al.A 77-GHz FMCW MIMO radar on SiGe single-chip transceiver［J］.IEEE Trans.on Microwave Theory and Techniques，2009，57（5）：1020- 1035.

［9］Huang Y，Brennan P V.FMCW based MIMO imaging radar for maritime navigation［J］.Progress in Electromagnetics Research，2011，115：327- 342.

［10］Guetlein J，Kirschner A，Detlefsen J.Motion compensation for a TDM FMCW MIMO radar system［C］∥Proc.of the 10th European Radar Conference，2013：37- 40.

［11］Klare J，Saalmann O，Wilden H，et al.First experimental results with the imaging MIMO radar MIRA-CLE X［C］∥Proc. of the 8th European Radar Conference，2010：1- 4.

［12］Mar J，Kuo C C，Wu S R.Implementation of the robust null extension for the SDR DBF of two-dimensional array antenna［C］∥Proc.of the International Conference on Electronic Devices，Systems and Applications，2010：26- 30.

［13］Roshanzamir A S，Bastani M H.Phased array radar beamforming method based on MIMO radar covariance［C］∥Proc.of the IET International Conference，2013：1- 6.

［14］Belfiori F，Hoogeboom P.Analysis of a novel MIMO system for security applications［C］∥Proc.of the IEEE International Symposium on Phase Array Systems&Technology，2010：1318- 1323.

［15］Wang Y L，Ding Q J，Li R F.Adaptive array processing［M］.Beijing：Tsinghua University Press，2009：28- 29.（王永良，丁前军，李荣峰.自适应阵列处理［M］.北京：清华大学出版社，2009：28- 29.）

［16］Henriksen S W.Radar-range equation［J］.Proceedings of the IEEE，1975，63（5）：813- 814.

Beamforming imaging algorithm for FMCW MIMO radar based on threshold

WANG Wei，LIANG Dong，LIU Qi，DU Dong-zhen，DUAN Hai-tao
（College of Automation，Harbin Engineering University，Harbin 150001，China）

To solve the problem that false alarms caused by the grating lobes of traditional beamforming algorithms appear in the angular dimension of frequency modulated continuous wave multiple-input multiple-output（FMCW MIMO）radar’s imaging results，an improved imaging algorithm based on azimuth threshold is proposed.First，the range information and azimuth information of targets are extracted from the original data separately，and then a detection threshold is applied to the azimuth data after normalization so as to limit the appearance of false targets in angular dimension.Finally，range information and azimuth information are combined with each other to obtain the imaging results.Imaging simulation proves that the false alarm probability is obviously reduced by the algorithm，and the results of field experiments further verify the remarkable imaging performance of the proposed algorithm.

multiple-input multiple-output（MIMO）radar；frequency modulated continuous wave（FMCW）；beamforming；false alarm；field imaging experiment

TN 958

10.3969／j.issn.1001-506X.2015.12.13

王伟（1979- ），男，教授，博士，主要研究方向为雷达信号处理。

E-mail：wangwei407＠hrbeu.edu.cn

梁栋（1991-），男，硕士研究生，主要研究方向为MIMO雷达成像技术、信号高速实时处理。

E-mail：liangd＠hrbeu.edu.cn

刘琦（1988-），男，硕士研究生，主要研究方向为MIMO雷达阵列信号处理。

E-mail：lq_skyven＠126.com

杜东贞（198-9- ），男，硕士研究生，主要研究方向为滑模控制理论。

E-mail：dudongzhen12345678＠163.com

段海涛（199-0- ），男，硕士研究生，主要研究方向为阵列信号处理。